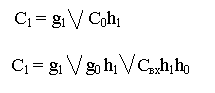|
|
Контрольная: Сумматор с параллельным переносом и автомат Мили
Контрольная: Сумматор с параллельным переносом и автомат Мили
Министерство общего и профессионального образования Самарский государственный технический университет Кафедра: Робототехнические системыКонтрольная работа Цифровые устройства и микропроцессоры Самара, 2001 |
|
1. Используя одноразрядные полные сумматоры построить функциональную
схему трехразрядного накапливающего сумматора с параллельным переносом.
РЕШЕНИЕ:
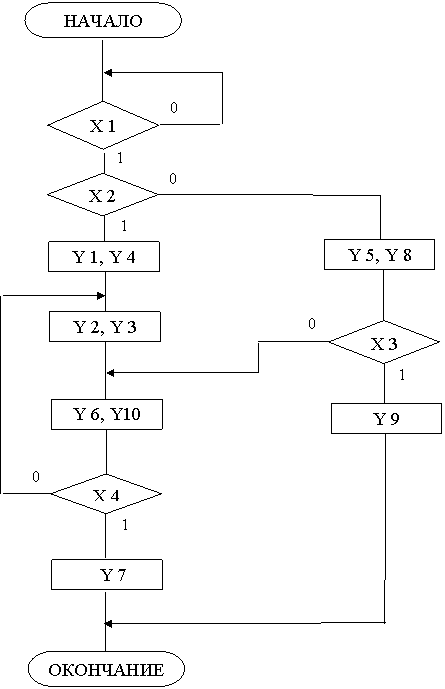
Одноразрядный сумматор рис.1 имеет три входа (два слагаемых и перенос из
предыдущего разряда) и два выхода (суммы и переноса в следующий разряд).
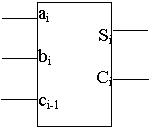 Таблица истинности одноразрядного сумматора. Таблица истинности одноразрядного сумматора.
| ai | bi | ci-1 | Si | Ci | | 0 | 0 | 0 | 0 | 0 | | 0 | 0 | 1 | 1 | 0 | | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 1 | 0 | 1 | | 1 | 0 | 0 | 1 | 0 | | 1 | 0 | 1 | 0 | 1 | | 1 | 1 | 0 | 0 | 1 | | 1 | 1 | 1 | 1 | 1 |
Сумматоры для параллельных операндов с параллельным переносом разработаны для
получения максимального быстродействия.
Для построения сумматора с параллельным переносом введем две вспомогательные
функции.
Функция генерации – принимает единичное значение если перенос на выходе
данного разряда появляется независимо от наличия или отсутствия входного
переноса.
Функция прозрачности – принимает единичное значение, если перенос на
выходе данного разряда появляется только при наличии входного переноса.
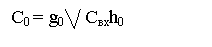 Сформируем перенос на выходе младшего разряда:
На выходе следующего разряда:
В базисе И-НЕ:
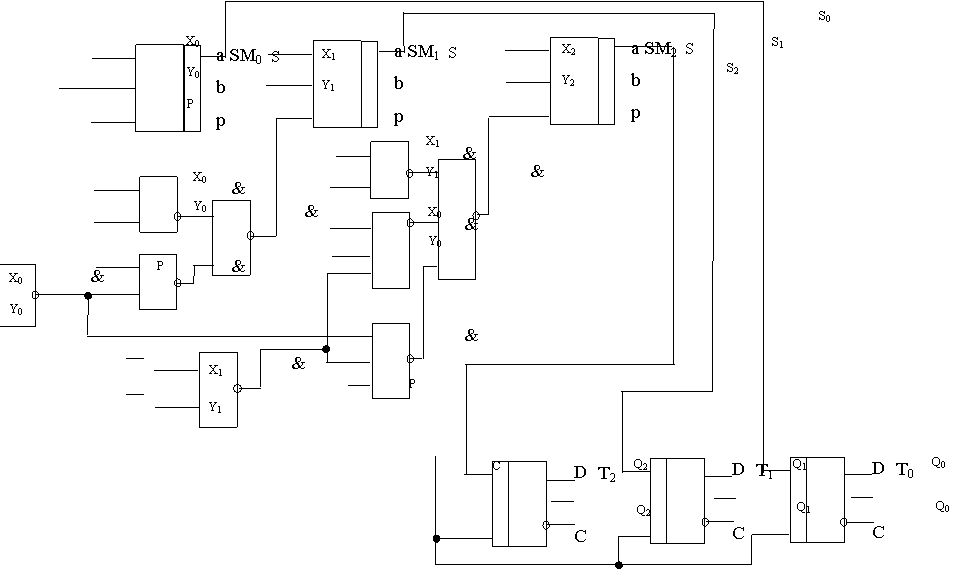
Накапливающий сумматор представляет собой сочетание сумматора и регистра.
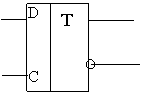
Регистр выполним на D-триггерах (рис. 2).
2. Сформируем перенос на выходе младшего разряда:
На выходе следующего разряда:
В базисе И-НЕ:
Накапливающий сумматор представляет собой сочетание сумматора и регистра.
Регистр выполним на D-триггерах (рис. 2).
2.
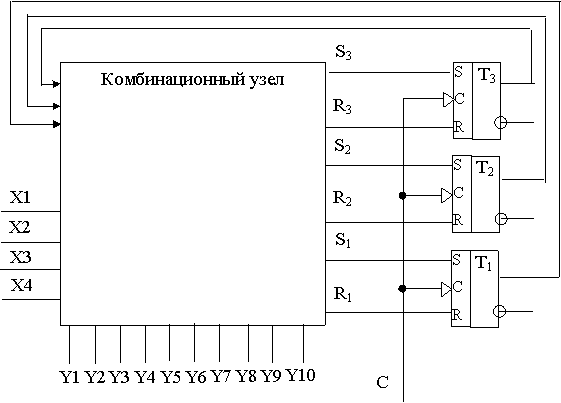
 3. Построить схему электрическую принципиальную управляющего автомата
Мили для следующей микропрограммы:
РЕШЕНИЕ:
1. Построение графа функционирования:
Управляющее устройство является логическим устройством последовательностного
типа. Микрокоманда выдаваемая в следующем тактовом периоде, зависит от
состояния в котором находится устройство. Для определения состояний
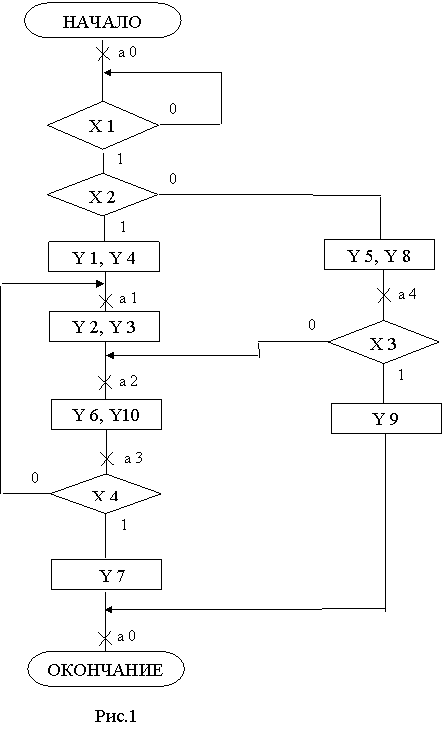
устройства произведем разметку схемы алгоритма, представленной в
микрокомандах (Рис. 1).
Полученные отметки а0, а1, а2, а3, а4 соответствуют состояниям устройства.
Устройство имеет пять состояний. Построим граф функционирования.
3. Построить схему электрическую принципиальную управляющего автомата
Мили для следующей микропрограммы:
РЕШЕНИЕ:
1. Построение графа функционирования:
Управляющее устройство является логическим устройством последовательностного
типа. Микрокоманда выдаваемая в следующем тактовом периоде, зависит от
состояния в котором находится устройство. Для определения состояний
устройства произведем разметку схемы алгоритма, представленной в
микрокомандах (Рис. 1).
Полученные отметки а0, а1, а2, а3, а4 соответствуют состояниям устройства.
Устройство имеет пять состояний. Построим граф функционирования.
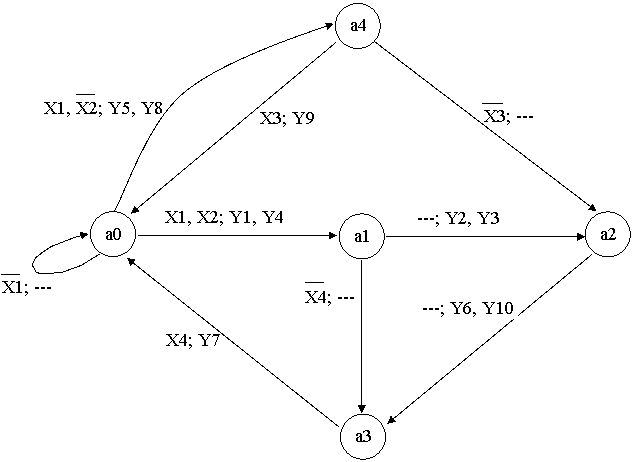 Кодирование состояний устройства.
Кодирование состояний устройства.
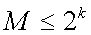 В процессе кодирования состояний каждому состоянию устройства должна быть поставлена в соответствие некоторая кодовая комбинация. Число разрядов кодов выбирается из следующего условия: , где М – число кодовых комбинаций, k – число разрядов. В процессе кодирования состояний каждому состоянию устройства должна быть поставлена в соответствие некоторая кодовая комбинация. Число разрядов кодов выбирается из следующего условия: , где М – число кодовых комбинаций, k – число разрядов.
В рассматриваемом устройстве М = 5 k = 3. | Таблица 1 | | Состояние | Кодовые комбинации | Q3 | Q2 | Q1 | | а0 | 0 | 0 | 0 | | а1 | 0 | 0 | 1 | | а2 | 0 | 1 | 0 | | а3 | 0 | 1 | 1 | | а4 | 1 | 0 | 0 |
Соответствие между состояниями устройства и кодовыми комбинациями зададим в
таблице 1.
2. Структурная схема управляющего устройства.
3. Построение таблицы функционирования.
| Текущее состояние | Следующее состояние | Условия перехода | Входные сигналы | | обозначение | Кодовая комбинация | обозначение | Кодовая комбинация | Сигналы установки триггеров | Управляющие микрокоманды | Q3 | Q2 | Q1 | Q3 | Q2 | Q1 | | а0 | 0 | 0 | 0 | а1 | 0 | 0 | 1 | Х1; Х2 | S1 | Y1; Y4 | а0 | 0 | 0 | 0 | а0 | 0 | 0 | 0 | Х1 | --- | --- | а0 | 0 | 0 | 0 | а4 | 1 | 0 | 0 | Х1; Х2 | S3 | Y5; Y8 | | а1 | 0 | 0 | 1 | а2 | 0 | 1 | 0 | --- | S2; R1 | Y2;Y3 | | а2 | 0 | 1 | 0 | а3 | 0 | 1 | 1 | --- | S1 | Y6;Y10 | | а3 | 0 | 1 | 1 | а0 | 0 | 0 | 0 | Х4 | R2; R1 | Y7 | а3 | 0 | 1 | 1 | а1 | 0 | 0 | 1 | Х4 | R2 | --- | | а4 | 1 | 0 | 0 | а0 | 0 | 0 | 0 | Х3 | R3 | Y9 | а4 | 1 | 0 | 0 | а2 | 0 | 1 | 0 | Х3 | R3; S2 | --- |
Таблица перехода RS триггера.
| Вид перехода триггера | Сигналы на входах триггера | | S | R |  0 0 0 0
| 0 | - |  0 1 0 1
| 1 | 0 |  1 0 1 0
| 0 | 1 |  1 1 1 1
| - | 0 |
4. Запишем логические выражения для выходных значений комбинационного узла.
S1 Y1 Y4 = a0 | S3 Y5 Y8 = X1 X2 a0 | S2 R1 Y2 Y3 = a1 | S1 Y6 Y10 = a2 | R2 R1 Y7 = X4 a3 | R2 = X4 a3 | R3 Y9 = X3 a4 | R3 S2 = X3 a4 |
Определим логическое выражение для каждой выходной величины.
S3 = X1 X2 a0 | S2 = a1 Ú X3 a4 | S1 = a0 Ú a1 | R3 = X3 a4 Ú X3 a4 | R2 = X4 a3 Ú X4 a3 | R1 = a1 Ú X4 a3 | | Y1 Y4 = a0 | Y5 Y8 = X1 X2 a0 | | Y2 Y3 = a1 | | Y6 Y10 = a2 | | Y7 = X4a3 | | Y9 = X3a4 |
5. Построение логической схемы комбинационного узла.
Входящие в выражения значения a0, a1, a2, a3, a4, определяемые комбинацией
значений Q3, Q2, Q1 могут быть получены с
помощью дешифратора.
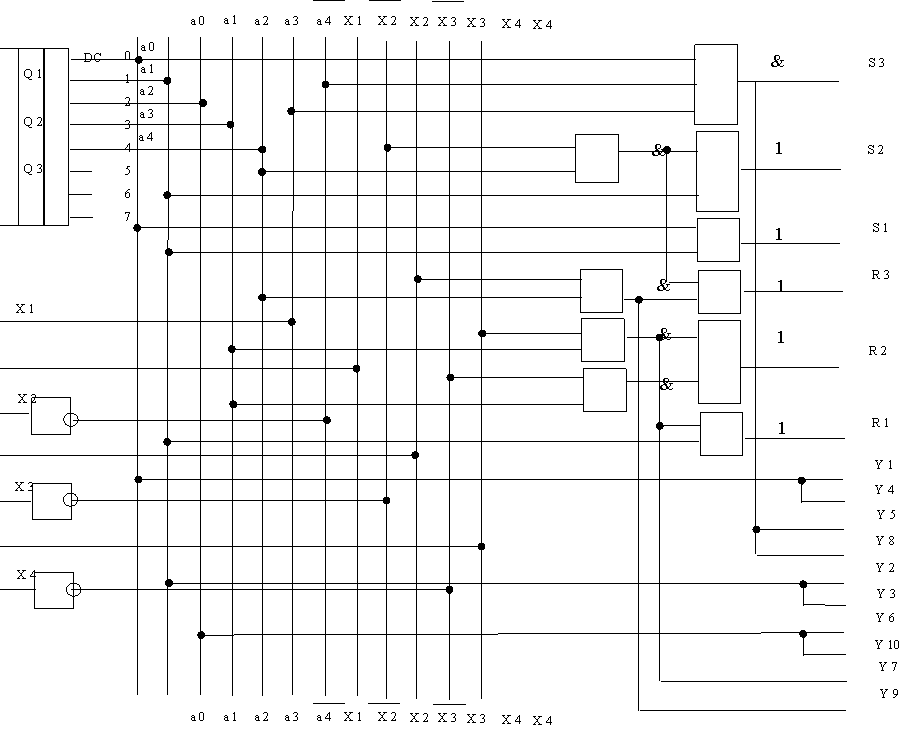
|

|

 3. Построить схему электрическую принципиальную управляющего автомата
Мили для следующей микропрограммы:
3. Построить схему электрическую принципиальную управляющего автомата
Мили для следующей микропрограммы:
 Кодирование состояний устройства.
Кодирование состояний устройства.
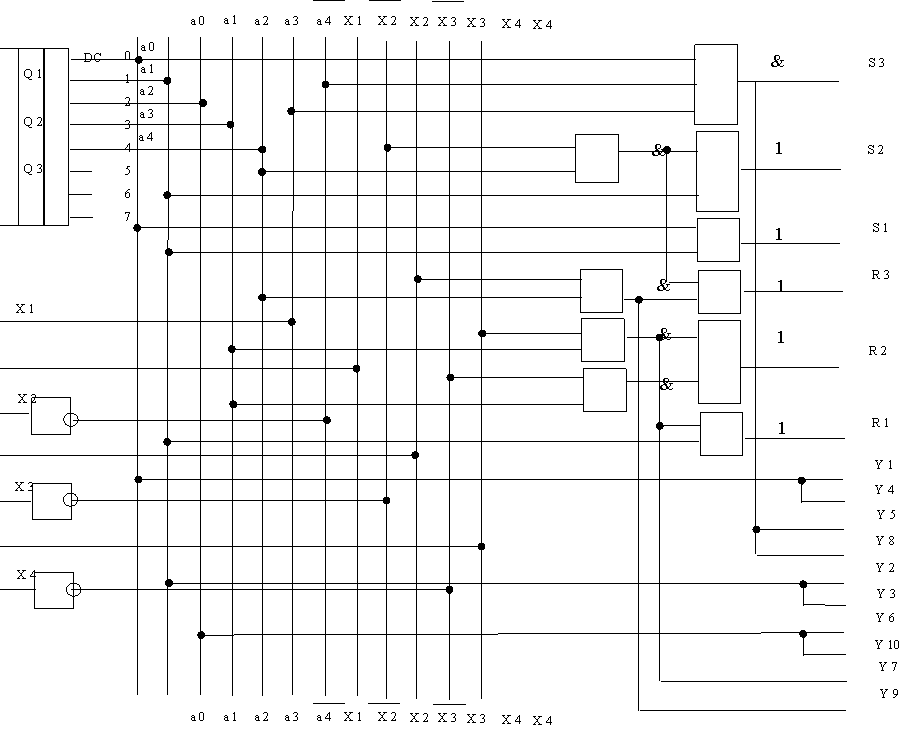
 Таблица истинности одноразрядного сумматора.
Таблица истинности одноразрядного сумматора.