Курсовая: Кодовый замок

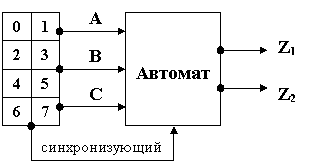
Содержание. 1). Задание на проектирование. -2- 2). Введение. -2- 3). Абстрактный синтез автомата. -5- 4). Структурный синтез автомата. -8- 5). Набор элементов для физического синтеза. -8- 6). Литература, дата, подпись. -8- Задание. Спроектировать автомат «кодовый замок», имеющий три информационных входа A, B, C, на которые подается входной сигнал в восьмеричном коде, и два выхода Z1, Z2. Z1 – возбуждается при подаче, на (A, B, C) входы, заданной последовательности сигналов. Z2 - возбуждается при нарушении заданной последовательности сигналов. В качестве элементной базы рекомендуется использовать RS и JK триггеры и интегральные микросхемы с набором логических элементов. После получения функциональной схемы следует провести анализ на возможные ложные комбинации и состязания в автомате. Для варианта № 6 принять следующую последовательность входных сигналов: 0 – 1 – 5 – 4 – 5 7 – 5 – 7 – 3 – 7 1 – 0 – 4 – 5 – 4 5 – 4 – 0 – 1 – 0 Введение в проблематику и методику проектирования автоматов с памятью Узлы и устройства, которые содержат элементы памяти, относятся к классу автоматов с памятью (АП). Наличие элементов памяти (ЭП) придает АП свойство иметь некоторое внутреннее состояние Q, определяемое совокупностью состояний всех элементов памяти. В зависимости от внутреннего состояния (далее называемого просто состоянием), АП различно реагирует на один и тот же вектор входных сигналов X. Воспринимая входные сигналы при определенном состоянии, АП переходит в новое состояние и вырабатывает вектор выходных переменных Y. Таким образом, для АП QH = f(Q, X) и Y = φ(Q, X), где QH и Q — состояния АП после и до подачи входных сигналов (индекс "н" от слова "новое"). Переходы АП из одного состояния в другое начинаются с некоторого исходного состояния Q0, задание которого также является частью задания автомата. Следующее состояние зависит от Q0 и поступивших входных сигналов X. В конечном счете, текущее состояние и выходы автомата зависят от начального состояния и всех векторов X, поступавших на автомат в предшествующих сменах входных сигналов. Таким образом, вся последовательность входных сигналов определяет последовательность состояний и выходных сигналов. Это объясняет название "последователъностные схемы", также применяемое для обозначения АП. Структурно АП отличаются от КЦ наличием в их схемах обратных связей, вследствие чего в них проявляются свойства запоминания состояний (полезно вспомнить схемы триггерных элементов, где указанная особенность проявляется очень наглядно). Автоматы с памятью в каноническом представлении разделяют на две части: память и комбинационную цепь. На входы КЦ подаются входные сигналы и сигналы состояния АП. На ее выходе вырабатываются выходные сигналы и сигналы перевода АП в новое состояние. Принципиальным является деление АП на асинхронные и синхронные. В асинхронных (рис. 1, а) роль элементов памяти играют элементы задержки, через которые сигналы состояния передаются на входы КЦ, чтобы совместно с новым набором входных переменных определить следующую пару значений Y и Q на выходе. Элементы АП переключаются здесь под непосредственным воздействием изменений информационных сигналов. Скорость распространения процесса переключений в цепях асинхронного автомата определяется собственными задержками элементов. В синхронном АП (рис. 1, б) имеются специальные синхросигналы (тактирующие импульсы) С, которые разрешают элементам памяти прием данных только в определенные моменты времени. Элементами памяти служат синхронные триггеры. Процесс обработки информации упорядочивается во времени, и в течение одного такта возможно распространение процесса переключения только в строго определенных пределах тракта обработки информации.

б)

а)

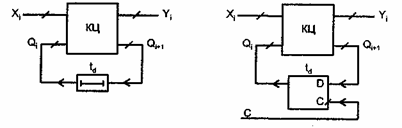Рис. 1. Асинхронный (а) и синхронный (б) автоматы с памятью Практическое применение асинхронных автоматов существенно затруднено сильным влиянием на их работу задержек сигналов в цепях АП, создающих статические и динамические риски, гонки элементов памяти (неодновременность срабатывания ЭП даже при одновременной подаче на них входных сигналов) и др. В итоге характерным свойством асинхронного автомата является то, что при переходе из одного устойчивого состояния в другое он обычно проходит через промежуточные нестабильные состояния. Нельзя сказать, что методы борьбы с нежелательными последствиями рисков и гонок в асинхронных АП отсутствуют, но все же обеспечение предсказуемого поведения АП — сложная проблема. В более или менее сложных АП асинхронные схемы встречаются очень редко, а в простейших схемах применяются. Примером могут служить асинхронные RS-триггеры. В синхронных автоматах каждое состояние устойчиво и переходные временные состояния не возникают. Концепция борьбы с последствиями рисков и гонок в синхронных автоматах проста — прием информации в элементы памяти разрешается только после завершения в схеме переходных процессов. Это обеспечивается параметрами синхроимпульсов, задающих интервалы времени для завершения тех или иных процессов. В сравнении с асинхронными, синхронные АП значительно проще в проектировании. На сегодняшний день и достаточно длительную перспективу основным путем построения АП следует считать применение тактирования, т. е. синхронных автоматов. В работах отечественных и зарубежных ученых разрабатывается направление, называемое проектированием самосинхронизирующихся устройств, в которых тактовые импульсы следуют с переменной частотой, зависящей от длительности реального переходного процесса в схеме. Однако перспективность этого направления еще не вполне ясна. В теории автоматов проводится их классификация по ряду признаков. Не вдаваясь в подробности, отметим, что в схемотехнике преобладают автоматы Мура, выходы которых являются функциями только состояния автомата. Для этого автомата Q H = f(Q, X) и Y = φ(Q). Зависимость выходов и от состояния автомата и от вектора входных переменных свойственна автоматам Мили. Некоторые функциональные узлы принадлежат к числу автономных автоматов, которые не имеют информационных входов, и под действием тактовых сигналов переходят из состояния в состояние по алгоритму, определяемому структурой автомата. В нашем случае, для формирования последовательности выходных сигналов Y = {Z1, Z2} при соответствующей последовательности входных сигналов (A, B, C)i, можно использовать автомат с жесткой логикой и законом функционирования автомата Мили:

Qt+1 = f(Qt, ABCt); Yt = φ(Qt, ABCt), где: Q = {Q1, Q2, Q3, Qn} – множество состояний автомата; t = 0, 1, 2, 3, 4,. I. Абстрактный синтез автомата.

1.1) Интерфейс автомата (рис. 2). 1.2) Алфавит состояний автомата

	D4	D3	D2	D1	D0
Q0	0	0	0	0	0
Q1	0	0	0	0	1
Q2	0	0	0	1	0
Q3	0	0	0	1	1
Q4	0	0	1	0	0
Q5	0	0	1	0	1
Q6	0	0	1	1	0
Q7	0	0	1	1	1
Q8	0	1	0	0	0
Q9	0	1	0	0	1
Q10	0	1	0	1	0
Q11	0	1	0	1	1
Q12	0	1	1	0	0
Q13	0	1	1	0	1
Q14	0	1	1	1	0
Q15	0	1	1	1	1
Q16	1	0	0	0	0

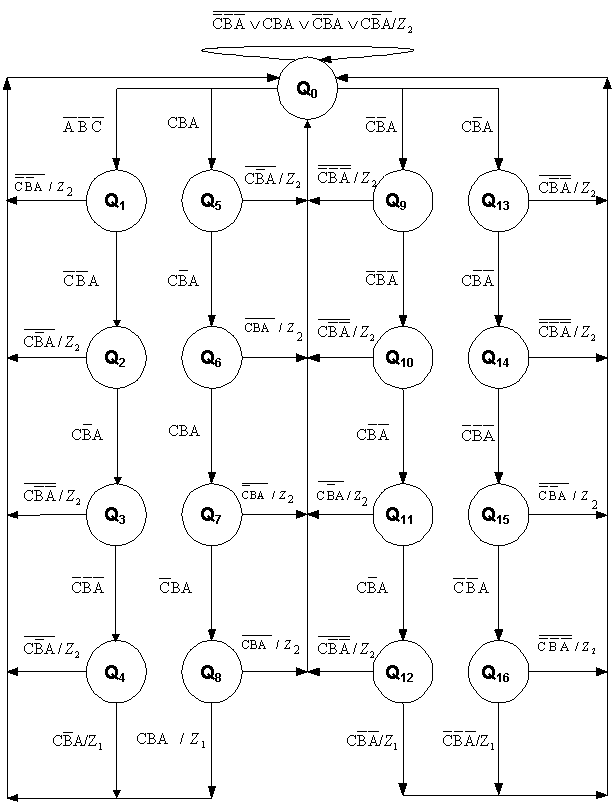
1.3) В соответствии с заданием и алфавитом состояний строим граф переходов

1.4) В соответствии с графом переходов и таблицей состояний строим таблицу переходов

Q						C	B	A	(CBA)	Z1	Z2	Qн
	D4	D3	D2	D1	D0	C	B	A	(CBA)	Z1	Z2	D4	D3	D2	D1	D0
Q0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	Q1
Q0	0	0	0	0	0	1	1	1	7	0	0	0	0	1	0	1	Q5
Q0	0	0	0	0	0	0	0	1	1	0	0	0	1	0	0	1	Q9
Q0	0	0	0	0	0	1	0	1	5	0	0	0	1	1	0	1	Q13
Q1	0	0	0	0	1	0	0	1	1	0	0	0	0	0	1	0	Q2
Q2	0	0	0	1	0	1	0	1	5	0	0	0	0	0	1	1	Q3
Q3	0	0	0	1	1	1	0	0	4	0	0	0	0	1	0	0	Q4
Q4	0	0	1	0	0	1	0	1	5	1	0	0	0	0	0	0	Q0/Z1
Q5	0	0	1	0	1	1	0	1	5	0	0	0	0	1	1	0	Q6
Q6	0	0	1	1	0	1	1	1	7	0	0	0	0	1	1	1	Q7
Q7	0	0	1	1	1	0	1	1	3	0	0	0	1	0	0	0	Q8
Q8	0	1	0	0	0	1	1	1	7	1	0	0	0	0	0	0	Q0/Z1
Q9	0	1	0	0	1	0	0	0	0	0	0	0	1	0	1	0	Q10
Q10	0	1	0	1	0	1	0	0	4	0	0	0	1	0	1	1	Q11
Q11	0	1	0	1	1	1	0	1	5	0	0	0	1	1	0	0	Q12
Q12	0	1	1	0	0	1	0	0	4	1	0	0	0	0	0	0	Q0/Z1
Q13	0	1	1	0	1	1	0	0	4	0	0	0	1	1	1	0	Q14
Q14	0	1	1	1	0	0	0	0	0	0	0	0	1	1	1	1	Q15
Q15	0	1	1	1	1	0	0	1	1	0	0	1	0	0	0	0	Q16
Q16	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	Q0/Z1

Чтобы не загромождать таблицу переходами в состояние Q0/Z2 , условимся, что при всех остальных комбинациях Q и CBA, не описанных в таблице, переход будет осуществляться так:

(CBA)

Qн

все другие комбинации

Q0/Z2

Далее можно было бы выводить функции переходов, минимизировать, упрощать, опять минимизировать. Но есть способ лучше – прошить все эти функции “как есть” в ПЗУ, а в качестве элементов памяти использовать параллельный регистр с двухступенчатыми D-триггерами. При этом состояние Q и сигналы CBA будут являться адресом ПЗУ, а Z1, Z2 и Qн – данными, которые необходимо записать по этому адресу. Во все же остальные адреса необходимо записать 01000000. II. Структурный синтез автомата. 2.1) Использование всех наборов исключает присутствие ложных комбинаций в функциональной схеме. 2.2) Введение дополнительного синхронизирующего провода в интерфейс автомата (рис № 2) позволяет использовать тактируемый регистр с двухступенчатыми триггерами, которые, в свою очередь, предотвращают возможные гонки в автомате. 2.3) На странице № 7 реализуем функциональную схему. III. Набор элементов для физического синтеза. В качестве элементной базы можно использовать регистры с разрядностью ≥ 7 и асинхронным сбросом, ПЗУ с разрядностью адресов ≥ 8 и разрядностью данных ≥ 7, например, соответственно, 74LS199 и 573РФ2. Остается добавить, что работоспособность автомата была проверена в системе проектирования электронных схем CircuitMaker Pro 6.0 IV. Литература. 1. Е.Угрюмов «Цифровая схемотехника», BHV 2000. «12» апреля 2001г. _________________

Схема автомата

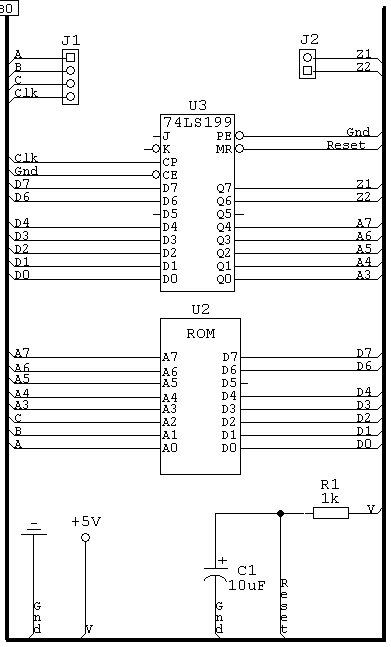Цепочка R1C1 обеспечивает сброс регистра и приведение автомата в исходное состояние при включении питания.

Рефераты

Курсовая: Кодовый замок

Курсовая: Кодовый замок

Схема автомата