|
|
Курсовая: Проектирование операционного устройства
K
B(i-1)P(i) C(i)A(i-1) | 00 | 01 | 11 | 10 | | 00 | * | * | * | * | | 01 | * | * | * | * | | 11 | 1 | 0 | 1 | 0 | | 10 | 0 | 1 | 0 | 1 |
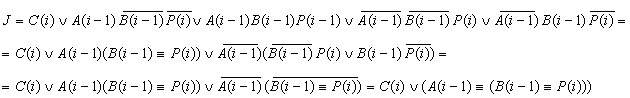
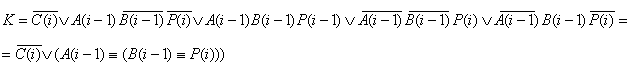
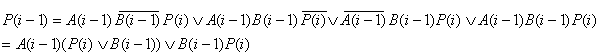 y4:
C(i):=C(i)+P(i)
y4:
C(i):=C(i)+P(i)
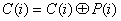 J=P(i)
K=P(i)
P(i-1)=C(i)P(i)
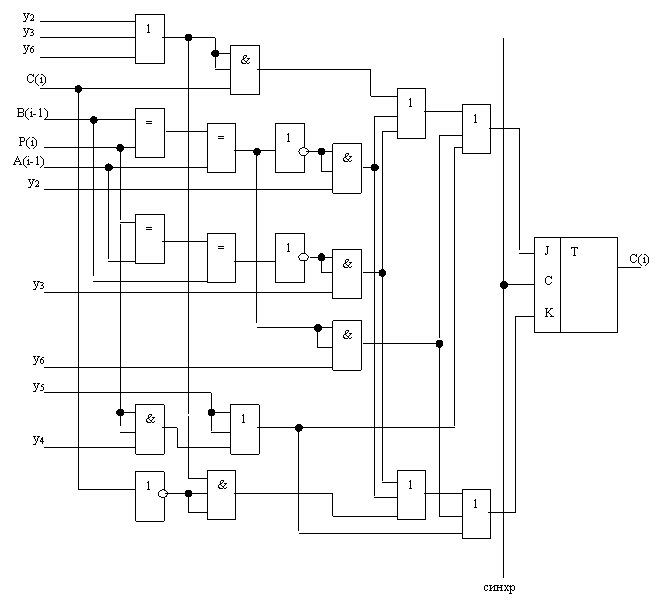
Составляются результирующие функции J, K и P(i-1), по ним на рис. 2.2.6.,
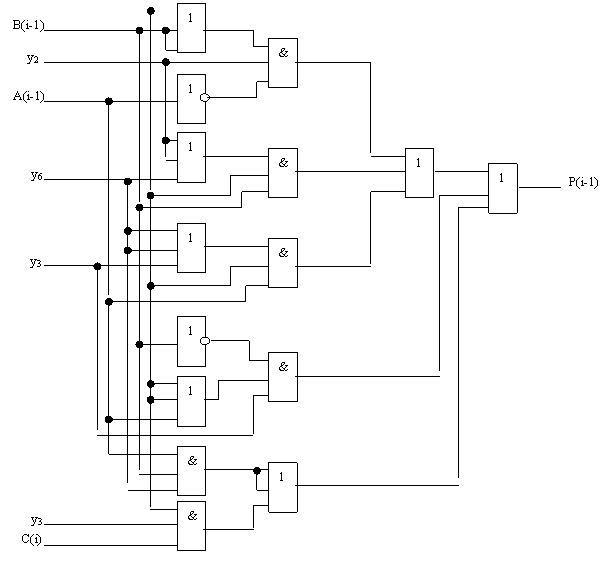
рис. 2.2.7. изображены логические схемы C(i), P(i-1), а на рис. 2.2.8. и рис.
2.2.9. соответственно даны их условные обозначения.
J=P(i)
K=P(i)
P(i-1)=C(i)P(i)
Составляются результирующие функции J, K и P(i-1), по ним на рис. 2.2.6.,
рис. 2.2.7. изображены логические схемы C(i), P(i-1), а на рис. 2.2.8. и рис.
2.2.9. соответственно даны их условные обозначения.
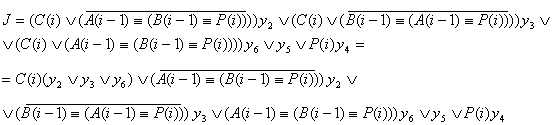
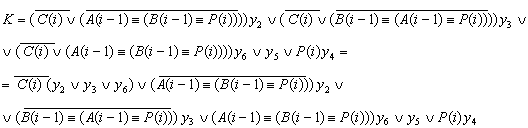
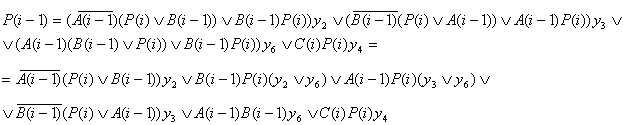 Рис. 2.2.6.
Рис. 2.2.7.
Рис. 2.2.8.
Рис. 2.2.9.
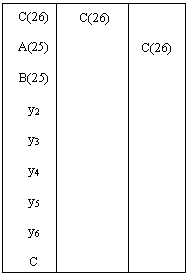
Поле С(26).
y2:
C(26):=ùA(25)+B(25)
В виде логической функции это получится так,
Рис. 2.2.6.
Рис. 2.2.7.
Рис. 2.2.8.
Рис. 2.2.9.
Поле С(26).
y2:
C(26):=ùA(25)+B(25)
В виде логической функции это получится так,
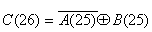 ,
Составляется таблица 13 функций возбуждения элементов памяти, по этой таблице
будет так же определяться функция переноса P(25).
Таблица 13 ,
Составляется таблица 13 функций возбуждения элементов памяти, по этой таблице
будет так же определяться функция переноса P(25).
Таблица 13
| t | t+1 | t | | C(26) | A(25) | B(25) | C(26) | P(25) | J | K | | 0 | 0 | 0 | 1 | 0 | 1 | 0Ú1 | | 0 | 0 | 1 | 0 | 1 | 0 | 0Ú1 | | 0 | 1 | 0 | 0 | 0 | 0 | 0Ú1 | | 0 | 1 | 1 | 1 | 0 | 1 | 0Ú1 | | 1 | 0 | 0 | 1 | 0 | 0Ú1 | 0 | | 1 | 0 | 1 | 0 | 1 | 0Ú1 | 1 | | 1 | 1 | 0 | 0 | 0 | 0Ú1 | 1 | | 1 | 1 | 1 | 1 | 0 | 0Ú1 | 0 |
Составляются функции:
J
А(25)В(25) С(26) | 00 | 01 | 11 | 10 | | 0 | 1 | | 1 | | | 1 | 1 | 1 | 1 | 1 |
K
А(25)В(25) С(26) | 00 | 01 | 11 | 10 | | 0 | 1 | 1 | 1 | 1 | | 1 | | 1 | | 1 |
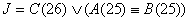
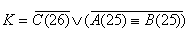
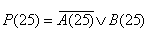 y3:
C(26):= A(25)+ ùB(25)
В виде логической функции это получится так,
y3:
C(26):= A(25)+ ùB(25)
В виде логической функции это получится так,
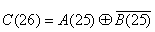 ,
Аналогично таблице 13 с заменой столбцов А(25) на В(25) и В(25) на А(25). ,
Аналогично таблице 13 с заменой столбцов А(25) на В(25) и В(25) на А(25).
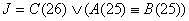
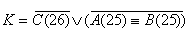
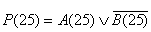 y4:
С(26):=С(26)+1,
y4:
С(26):=С(26)+1,
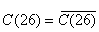 Таблица идентична таблице 11, соответственно функции имеют вид,
J=1, K=1, P(25)=C(26).
y5:
С(26):=ùС(26),
Таблица идентична таблице 11, соответственно функции имеют вид,
J=1, K=1, P(25)=C(26).
y5:
С(26):=ùС(26),
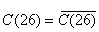 Таблица идентична таблице 11, соответственно функции имеют вид,
J=1, K=1.
y2:
C(26):=A(25)+B(25)
В виде логической функции это получится так,
Таблица идентична таблице 11, соответственно функции имеют вид,
J=1, K=1.
y2:
C(26):=A(25)+B(25)
В виде логической функции это получится так,
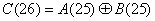 ,
Составляется таблица 14 функций возбуждения элементов памяти, по этой таблице
будет так же определяться функция переноса P(25).
Таблица 14 ,
Составляется таблица 14 функций возбуждения элементов памяти, по этой таблице
будет так же определяться функция переноса P(25).
Таблица 14
| t | t+1 | t | | C(26) | A(25) | B(25) | C(26) | P(25) | J | K | | 0 | 0 | 0 | 0 | 0 | 0 | 0Ú1 | | 0 | 0 | 1 | 1 | 0 | 1 | 0Ú1 | | 0 | 1 | 0 | 1 | 0 | 1 | 0Ú1 | | 0 | 1 | 1 | 0 | 1 | 0 | 0Ú1 | | 1 | 0 | 0 | 0 | 0 | 0Ú1 | 1 | | 1 | 0 | 1 | 1 | 0 | 0Ú1 | 0 | | 1 | 1 | 0 | 1 | 0 | 0Ú1 | 0 | | 1 | 1 | 1 | 0 | 1 | 0Ú1 | 1 |
Составляются функции:
J
А(25)В(25) С(26) | 00 | 01 | 11 | 10 | | 0 | | 1 | | 1 | | 1 | 1 | 1 | 1 | 1 |
K
А(25)В(25) С(26) | 00 | 01 | 11 | 10 | | 0 | 1 | 1 | 1 | 1 | | 1 | 1 | | 1 | |
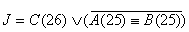
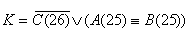
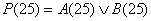 Составляются результирующие функции J, K и P(25), по ним на рис. 2.2.10.,
рис. 2.2.11. изображены логические схемы C(26), P(25) соответственно, а на
рис. 2.2.12. и рис. 2.2.13. соответственно даны их условные обозначения.
Составляются результирующие функции J, K и P(25), по ним на рис. 2.2.10.,
рис. 2.2.11. изображены логические схемы C(26), P(25) соответственно, а на
рис. 2.2.12. и рис. 2.2.13. соответственно даны их условные обозначения.
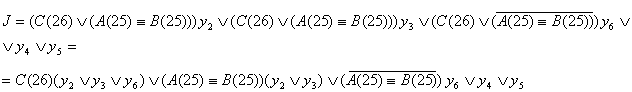
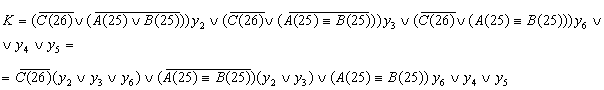
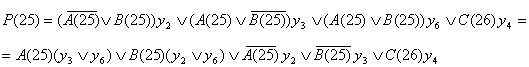
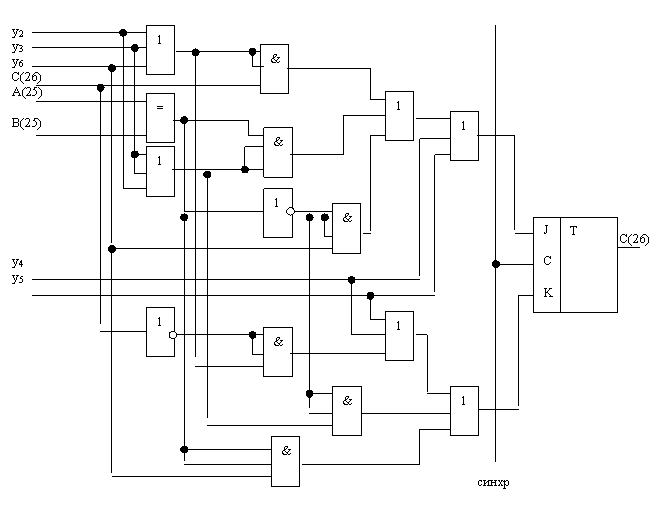 Рис. 2.2.10.
Рис. 2.2.10.
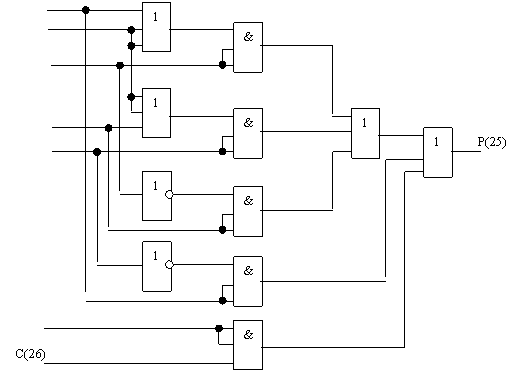 Рис. 2.2.11.
Рис. 2.2.12.
Рис. 2.2.13.
3.Разработка функциональной схемы управляющего автомата
3.1 Структурная схема управляющего автомата
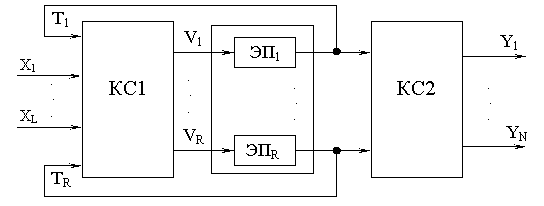
В структурном отношении управляющий автомат типа Мура может быть представлен
в виде, изображенном на рис. 3.1.1.
Рис. 3.1.1.
Память П автомата образуют элементарные полные автоматы Мура – элементы памяти
(ЭП), которые являются JK–триггерами. Каждому состоянию автомата Аf
(Аf
Рис. 2.2.11.
Рис. 2.2.12.
Рис. 2.2.13.
3.Разработка функциональной схемы управляющего автомата
3.1 Структурная схема управляющего автомата
В структурном отношении управляющий автомат типа Мура может быть представлен
в виде, изображенном на рис. 3.1.1.
Рис. 3.1.1.
Память П автомата образуют элементарные полные автоматы Мура – элементы памяти
(ЭП), которые являются JK–триггерами. Каждому состоянию автомата Аf
(Аf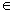 А, где А, где 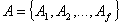 - множество состояний автомата) ставится в соответствие вектор длины R (R –
количество элементов памяти, образующих память автомата), компонентами которого
являются состояния ЭП автоиата T1, T2, .,TR.
Переход управляющего автомата из состояния Аd в Аf
осуществляется под действием входного сигнала, кодируемого вектором длины L;
компонентами этого вектора являются состояния входов x1, x2
, .,xL. При этом на выходе автомата формируется выходной сигнал,
кодируемый вектором длины N; компонентами этого вектора являются состояния
выходов Y1, Y2, .,YL. Изменения состояния на
переходе
- множество состояний автомата) ставится в соответствие вектор длины R (R –
количество элементов памяти, образующих память автомата), компонентами которого
являются состояния ЭП автоиата T1, T2, .,TR.
Переход управляющего автомата из состояния Аd в Аf
осуществляется под действием входного сигнала, кодируемого вектором длины L;
компонентами этого вектора являются состояния входов x1, x2
, .,xL. При этом на выходе автомата формируется выходной сигнал,
кодируемый вектором длины N; компонентами этого вектора являются состояния
выходов Y1, Y2, .,YL. Изменения состояния на
переходе 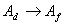 происходит под действием сигналов из множества
происходит под действием сигналов из множества 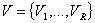 , формируемых на выходах схемы КС1.
Схема КС2 может быть реализована в виде стандартного блока – дешифратора,
выполняющего функции дешифрации состояний автомата: некоторому состоянию А
f ставится в соответствие сигнал Yr=1 на выходе дешифратора.
3.2 Закодированная граф – схема и граф управляющего автомата
Исходной информацией для определения числа входов, выходов и различных
состояний, в которых может находиться управляющий автомат, является
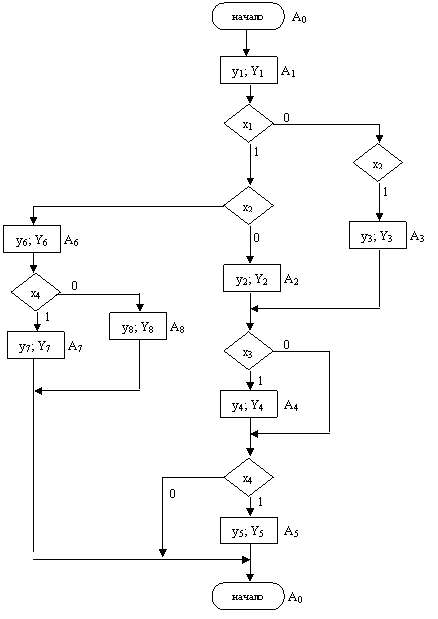
содержательный граф алгоритма, представленный закодированной граф – схемой
алгоритма (ГСА).Каждой операторной вершине содержательного графа можно
поставить в соответствие состояние автомата и выходной сигнал Yn;
условной вершине ставится в соответствие вход xl управляющего
автомата. ГСА, эквивалентная содержательному графу изображена на рис. 3.2.1.
Рис. 3.2.1.
Существуют различные методы структурного синтеза управляющего автомата. Одним из
таких методов является графический метод синтеза. Автомат представляется в виде
графа. Количество вершин графа соответствует количеству различных отметок A
f на ГСА автомата. Производится кодирование состояний автомата векторами
длины
, формируемых на выходах схемы КС1.
Схема КС2 может быть реализована в виде стандартного блока – дешифратора,
выполняющего функции дешифрации состояний автомата: некоторому состоянию А
f ставится в соответствие сигнал Yr=1 на выходе дешифратора.
3.2 Закодированная граф – схема и граф управляющего автомата
Исходной информацией для определения числа входов, выходов и различных
состояний, в которых может находиться управляющий автомат, является
содержательный граф алгоритма, представленный закодированной граф – схемой
алгоритма (ГСА).Каждой операторной вершине содержательного графа можно
поставить в соответствие состояние автомата и выходной сигнал Yn;
условной вершине ставится в соответствие вход xl управляющего
автомата. ГСА, эквивалентная содержательному графу изображена на рис. 3.2.1.
Рис. 3.2.1.
Существуют различные методы структурного синтеза управляющего автомата. Одним из
таких методов является графический метод синтеза. Автомат представляется в виде
графа. Количество вершин графа соответствует количеству различных отметок A
f на ГСА автомата. Производится кодирование состояний автомата векторами
длины 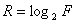 (где F –
мощность множества А), компонентами которых являются состояния T1,
.,TR ЭП. Полученные в результате кодирования векторы длины R
записываются в соответствующие вершины графа. (где F –
мощность множества А), компонентами которых являются состояния T1,
.,TR ЭП. Полученные в результате кодирования векторы длины R
записываются в соответствующие вершины графа.
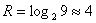 Связь между TR и Af показана в таблице 15, DC – дешифратор.
Таблица 15
Связь между TR и Af показана в таблице 15, DC – дешифратор.
Таблица 15
A T | A0 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | T1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | T2 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | T3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | T4 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | | Выход DC | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
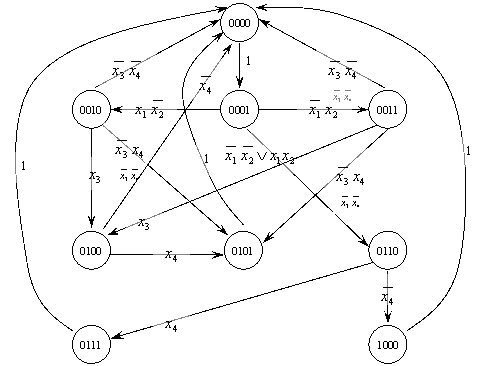
Путям перехода в ГСА на графе соответствуют дуги, указывающие направления
перехода.
Если в ГСА на пути перехода из вершины с отметкой Ad в вершину с
отметкой Af находятся условные вершины, отмеченные символами x
l, то на дугах графа записываются конъюнкции, ранг которых определяется
числом условных вершин, через которые проходит путь перехода. При xl
=0 в конъюнкции появится член 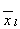 , в при xl=1 его прямое значение.
Граф управляющего автомата представлен на рис. 3.2.2.
Рис. 3.2.2.
3.3. Синтез комбинационных схем, реализующих функции возбуждения элементов
памяти управляющего автомата
Количество ЭП, составляющих память автомата, определяется по выражению
, в при xl=1 его прямое значение.
Граф управляющего автомата представлен на рис. 3.2.2.
Рис. 3.2.2.
3.3. Синтез комбинационных схем, реализующих функции возбуждения элементов
памяти управляющего автомата
Количество ЭП, составляющих память автомата, определяется по выражению
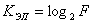 ,
где F – мощность множества А. ,
где F – мощность множества А.
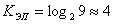 Для каждого TR (где
Для каждого TR (где 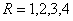 ) по графу составляется каноническая таблица функций переходов и выходов, а на
основе этих таблиц составляются функции возбуждения ЭП. Соответственно для T
1, T2, T3, T4 это будут таблицы 16, 17,
18, 19.
Таблица 16
) по графу составляется каноническая таблица функций переходов и выходов, а на
основе этих таблиц составляются функции возбуждения ЭП. Соответственно для T
1, T2, T3, T4 это будут таблицы 16, 17,
18, 19.
Таблица 16
| A | x1 | x2 | x3 | x4 | T1(t) | T1(t+1) | J1 | K1 | A0 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 | A1 | 1 | 0 | --- | --- | 0 | 0 | 0 | 0Ú1 | | 0 | 1 | --- | --- | 0 | 0 | 0 | 0Ú1 | | 0 | 0 | --- | --- | 0 | 0 | 0 | 0Ú1 | | 1 | 1 | --- | --- | 0 | 0 | 0 | 0Ú1 | A2 | --- | --- | 0 | 0 | 0 | 0 | 0 | 0Ú1 | | --- | --- | 1 | --- | 0 | 0 | 0 | 0Ú1 | | --- | --- | 0 | 1 | 0 | 0 | 0 | 0Ú1 | A3 | --- | --- | 0 | 0 | 0 | 0 | 0 | 0Ú1 | | --- | --- | 1 | --- | 0 | 0 | 0 | 0Ú1 | | --- | --- | 0 | 1 | 0 | 0 | 0 | 0Ú1 | A4 | --- | --- | --- | 0 | 0 | 0 | 0 | 0Ú1 | | --- | --- | --- | 1 | 0 | 0 | 0 | 0Ú1 | A5 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 | A6 | --- | --- | --- | 1 | 0 | 0 | 0 | 0Ú1 | | --- | --- | --- | 0 | 0 | 1 | 1 | 0Ú1 | A7 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 | A8 | --- | --- | --- | --- | 1 | 0 | 0Ú1 | 0 |
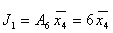
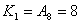 Таблица 17
Таблица 17
| A | x1 | x2 | x3 | x4 | T2(t) | T2(t+1) | J2 | K2 | A0 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 | A1 | 1 | 0 | --- | --- | 0 | 0 | 0 | 0Ú1 | | 0 | 1 | --- | --- | 0 | 0 | 0 | 0Ú1 | | 0 | 0 | --- | --- | 0 | 1 | 1 | 0Ú1 | | 1 | 1 | --- | --- | 0 | 1 | 1 | 0Ú1 | A2 | --- | --- | 0 | 0 | 0 | 0 | 0 | 0Ú1 | | --- | --- | 1 | --- | 0 | 1 | 1 | 0Ú1 | | --- | --- | 0 | 1 | 0 | 1 | 1 | 0Ú1 | A3 | --- | --- | 0 | 0 | 0 | 0 | 0 | 0Ú1 | | --- | --- | 1 | --- | 0 | 1 | 1 | 0Ú1 | | --- | --- | 0 | 1 | 0 | 1 | 1 | 0Ú1 | A4 | --- | --- | --- | 0 | 1 | 0 | 0Ú1 | 1 | | --- | --- | --- | 1 | 1 | 1 | 0Ú1 | 0 | A5 | --- | --- | --- | --- | 1 | 0 | 0Ú1 | 1 | A6 | --- | --- | --- | 1 | 1 | 1 | 0Ú1 | 0 | | --- | --- | --- | 0 | 1 | 0 | 0Ú1 | 1 | A7 | --- | --- | --- | --- | 1 | 0 | 0Ú1 | 1 | A8 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 |
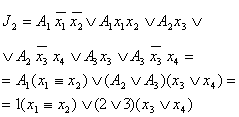
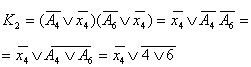 Таблица 18
Таблица 18
| A | x1 | x2 | x3 | x4 | T3(t) | T3(t+1) | J3 | K3 | A0 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 | A1 | 1 | 0 | --- | --- | 0 | 1 | 1 | 0Ú1 | | 0 | 1 | --- | --- | 0 | 1 | 1 | 0Ú1 | | 0 | 0 | --- | --- | 0 | 1 | 1 | 0Ú1 | | 1 | 1 | --- | --- | 0 | 1 | 1 | 0Ú1 | A2 | --- | --- | 0 | 0 | 1 | 0 | 0Ú1 | 1 | | --- | --- | 1 | --- | 1 | 0 | 0Ú1 | 1 | | --- | --- | 0 | 1 | 1 | 0 | 0Ú1 | 1 | A3 | --- | --- | 0 | 0 | 1 | 0 | 0Ú1 | 1 | | --- | --- | 1 | --- | 1 | 0 | 0Ú1 | 1 | | --- | --- | 0 | 1 | 1 | 0 | 0Ú1 | 1 | A4 | --- | --- | --- | 0 | 0 | 0 | 0 | 0Ú1 | | --- | --- | --- | 1 | 0 | 0 | 0 | 0Ú1 | A5 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 | A6 | --- | --- | --- | 1 | 1 | 1 | 0Ú1 | 0 | | --- | --- | --- | 0 | 1 | 0 | 0Ú1 | 1 | A7 | --- | --- | --- | --- | 1 | 0 | 0Ú1 | 1 | A8 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 |
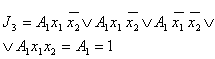
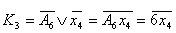 Таблица 19
Таблица 19
| A | x1 | x2 | x3 | x4 | T4(t) | T4(t+1) | J4 | K4 | A0 | --- | --- | --- | --- | 0 | 1 | 1 | 0Ú1 | A1 | 1 | 0 | --- | --- | 1 | 0 | 0Ú1 | 1 | | 0 | 1 | --- | --- | 1 | 1 | 0Ú1 | 0 | | 0 | 0 | --- | --- | 1 | 0 | 0Ú1 | 1 | | 1 | 1 | --- | --- | 1 | 0 | 0Ú1 | 1 | A2 | --- | --- | 0 | 0 | 0 | 0 | 0 | 0Ú1 | | --- | --- | 1 | --- | 0 | 0 | 0 | 0Ú1 | | --- | --- | 0 | 1 | 0 | 1 | 1 | 0Ú1 | A3 | --- | --- | 0 | 0 | 1 | 0 | 0Ú1 | 1 | | --- | --- | 1 | --- | 1 | 0 | 0Ú1 | 1 | | --- | --- | 0 | 1 | 1 | 1 | 0Ú1 | 0 | A4 | --- | --- | --- | 0 | 0 | 0 | 0 | 0Ú1 | | --- | --- | --- | 1 | 0 | 1 | 1 | 0Ú1 | A5 | --- | --- | --- | --- | 1 | 0 | 0Ú1 | 1 | A6 | --- | --- | --- | 1 | 0 | 1 | 1 | 0Ú1 | | --- | --- | --- | 0 | 0 | 0 | 0 | 0Ú1 | A7 | --- | --- | --- | --- | 1 | 0 | 0Ú1 | 1 | A8 | --- | --- | --- | --- | 0 | 0 | 0 | 0Ú1 |
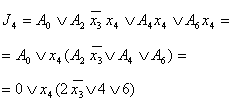
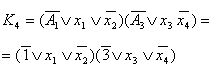 Функциональная схема управляющего автомата приведена на функциональной схеме
операционного устройства, где показаны связи между операционным и управляющим
автоматами.
4. Функциональная схема операционного устройства
4.1. Организация связи между операционным и управляющим автоматами
Связи между операционным и управляющим автоматами организуются так. Сигналы с
выходов управляющего автомата подаются на его же входы, а также на входы
операционного автомата. На входы управляющего автомата подаются также сигналы
логических условий. Каждая микрооперация выполняется строго при поступлении
синхроимпульса и при подаче соответствующего управляющего сигнала, который в
свою очередь вырабатывается на основе сигналов логических условий,
вычисленных в предыдущий такт работы операционного устройства.
Графически связи между операционным и управляющим автоматами показаны на
функциональной схеме операционного устройства, приведенной на
масштабно–координатной бумаге.
4.2. Описание работы операционного устройства на заданном отрезке времени
Дано:
А=1.1010010
В=0.0011101
После выполнения микрооперации y1 на входы управляющего автомата
приходит сигнал Y1 и сигналы логических условий,
Функциональная схема управляющего автомата приведена на функциональной схеме
операционного устройства, где показаны связи между операционным и управляющим
автоматами.
4. Функциональная схема операционного устройства
4.1. Организация связи между операционным и управляющим автоматами
Связи между операционным и управляющим автоматами организуются так. Сигналы с
выходов управляющего автомата подаются на его же входы, а также на входы
операционного автомата. На входы управляющего автомата подаются также сигналы
логических условий. Каждая микрооперация выполняется строго при поступлении
синхроимпульса и при подаче соответствующего управляющего сигнала, который в
свою очередь вырабатывается на основе сигналов логических условий,
вычисленных в предыдущий такт работы операционного устройства.
Графически связи между операционным и управляющим автоматами показаны на
функциональной схеме операционного устройства, приведенной на
масштабно–координатной бумаге.
4.2. Описание работы операционного устройства на заданном отрезке времени
Дано:
А=1.1010010
В=0.0011101
После выполнения микрооперации y1 на входы управляющего автомата
приходит сигнал Y1 и сигналы логических условий, 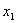 =1 и
=1 и 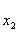 =0, под
действием этих сигналов и при поступлении синхроимпульса из генератора
синхроимпульсов (ГСИ) триггеры управляющего автомата переходят в состояния: T
1=0, T2=0, T3=1, T4=0 (см. общую схему).
В свою очередь на дешифраторе вырабатывается сигнал Y2, при котором
в операционном автомате выполняется микрооперация y2.
Которая заключается в следующем. Полю С(1) присваивается значение переноса в
этот разряд P(1), который можно вычислить по схеме на рис. 2.2.5., а схема
С(1) изображена на рис. 2.2.1. Полю С(2) присваивается значение инверсии
переноса в этот разряд P(2) (рис. 2.2.7.), схема С(2) изображена на рис.
2.2.3. На поле С(3:25) происходит присвоение C(i) суммы B(i-1), инверсии A(i-
1) и переноса P(i)(схема для С(i) на рис. 2.2.6., а для P(i) на рис. 2.2.7),
где i = 3-25. Но перенос P(25) определяется иначе, на основе схемы рис.
2.2.11. На поле С(26) происходит подобная операция (С(26):=А(25)+В(25))
только без учета переноса, так как его не может быть (С(26) – последний
разряд), схема дана на рис. 2.2.10. В результате этой микрооперации слово С
принимает следующий вид: С=01.1001010
Далее на входы управляющего автомата подается сигнал y2 и сигналы
логических условий =0, под
действием этих сигналов и при поступлении синхроимпульса из генератора
синхроимпульсов (ГСИ) триггеры управляющего автомата переходят в состояния: T
1=0, T2=0, T3=1, T4=0 (см. общую схему).
В свою очередь на дешифраторе вырабатывается сигнал Y2, при котором
в операционном автомате выполняется микрооперация y2.
Которая заключается в следующем. Полю С(1) присваивается значение переноса в
этот разряд P(1), который можно вычислить по схеме на рис. 2.2.5., а схема
С(1) изображена на рис. 2.2.1. Полю С(2) присваивается значение инверсии
переноса в этот разряд P(2) (рис. 2.2.7.), схема С(2) изображена на рис.
2.2.3. На поле С(3:25) происходит присвоение C(i) суммы B(i-1), инверсии A(i-
1) и переноса P(i)(схема для С(i) на рис. 2.2.6., а для P(i) на рис. 2.2.7),
где i = 3-25. Но перенос P(25) определяется иначе, на основе схемы рис.
2.2.11. На поле С(26) происходит подобная операция (С(26):=А(25)+В(25))
только без учета переноса, так как его не может быть (С(26) – последний
разряд), схема дана на рис. 2.2.10. В результате этой микрооперации слово С
принимает следующий вид: С=01.1001010
Далее на входы управляющего автомата подается сигнал y2 и сигналы
логических условий 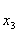 =0 и
=0 и 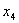 =1. Тогда при
поступлении сигнала из ГСИ и сигнала Y2 триггеры управляющего
автомата переходят в состояния: T1=0, T2=1, T3
=0, T4=1, что на выходе дешифратора соответствует сигналу Y5
, под действием которого в операционном автомате выполняется микрооперация y
5 (см. общую схему).
При этой микрооперации значения полей С(1) и С(2) не меняются, см.
соответственно рис. 2.2.1.и рис. 2.2.3. Разрядам полей С(3:25) и С(26)
присваивается значение инверсии этих разрядов, что можно вычислить из схем на
соответственно рис. 2.2.6. и рис. 2.2.10. Тогда в данном примере значение
слова С будет таким: С=01.0110101
Далее, когда на входы управляющего автомата приходит сигнал Y5 и
сигнал из ГСИ, триггеры управляющего автомата обнуляются, то есть T1
=0, T2=0, T3=0, T4=0, а на выходе дешифратора
вырабатывается сигнал Y0 (см. общую схему), который означает, что
операционное устройство готово к выполнению следующего цикла операции
арифметического сложения чисел с фиксированной запятой в обратных двоичных
кодах.
Примечание.
В примере использовались восьмиразрядные слова А и В, а также девятиразрядное
слово С , то есть полю С(3:25) соответствует поле С(3:8), а полю С(26) поле
С(9).
Заключение
В данном курсовом проекте разработано операционное устройство, выполняющее
операцию арифметического сложения чисел с фиксированной запятой в обратных
двоичных кодах. Также приведена общая схема устройства, состоящая из двух
главных частей: операционного автомата и управляющего автомата. В работе
предполагалось, что вся информация, необходимая для выполнения операции
(операнды А и В), была уже занесена в память устройства.
Литература
1. Проф. А. А. Эйлер, доц. Р. С. Ефимова, ст. преп. В. В. Жевержеева
Методические указания к выполнению курсовой работы по дисциплине
"Арифметические и логические основы цифровых автоматов". Ленинград: ЛИИЖТ,
1983
2. Б. Г. Лысиков Арифметические и логические основы цифровых автоматов
Минск: Высшая школа, 1980
Приложение
Прокрутка алгоритма операции приведена в таблице 20.
Таблица 20 =1. Тогда при
поступлении сигнала из ГСИ и сигнала Y2 триггеры управляющего
автомата переходят в состояния: T1=0, T2=1, T3
=0, T4=1, что на выходе дешифратора соответствует сигналу Y5
, под действием которого в операционном автомате выполняется микрооперация y
5 (см. общую схему).
При этой микрооперации значения полей С(1) и С(2) не меняются, см.
соответственно рис. 2.2.1.и рис. 2.2.3. Разрядам полей С(3:25) и С(26)
присваивается значение инверсии этих разрядов, что можно вычислить из схем на
соответственно рис. 2.2.6. и рис. 2.2.10. Тогда в данном примере значение
слова С будет таким: С=01.0110101
Далее, когда на входы управляющего автомата приходит сигнал Y5 и
сигнал из ГСИ, триггеры управляющего автомата обнуляются, то есть T1
=0, T2=0, T3=0, T4=0, а на выходе дешифратора
вырабатывается сигнал Y0 (см. общую схему), который означает, что
операционное устройство готово к выполнению следующего цикла операции
арифметического сложения чисел с фиксированной запятой в обратных двоичных
кодах.
Примечание.
В примере использовались восьмиразрядные слова А и В, а также девятиразрядное
слово С , то есть полю С(3:25) соответствует поле С(3:8), а полю С(26) поле
С(9).
Заключение
В данном курсовом проекте разработано операционное устройство, выполняющее
операцию арифметического сложения чисел с фиксированной запятой в обратных
двоичных кодах. Также приведена общая схема устройства, состоящая из двух
главных частей: операционного автомата и управляющего автомата. В работе
предполагалось, что вся информация, необходимая для выполнения операции
(операнды А и В), была уже занесена в память устройства.
Литература
1. Проф. А. А. Эйлер, доц. Р. С. Ефимова, ст. преп. В. В. Жевержеева
Методические указания к выполнению курсовой работы по дисциплине
"Арифметические и логические основы цифровых автоматов". Ленинград: ЛИИЖТ,
1983
2. Б. Г. Лысиков Арифметические и логические основы цифровых автоматов
Минск: Высшая школа, 1980
Приложение
Прокрутка алгоритма операции приведена в таблице 20.
Таблица 20
Пункт алгоритма | Выполнение микрооперации или вычисление лог. условия | Условие перехода | Пункт перехода | Коментарии | | 1 | 2 | 3 | 4 | 5 | | 1 | А:=0.0011101 В:=0.1010010 | Безуслов | 2 | Операнды с одинаковыми знаками (положительные) | | 2 | П(1):=0 С(1):=0 | Безуслов | 3 | Обнуление | | 3 | А(1)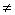 1 1 | x1=0 | 5 | Проверка знака слова А | | 5 | В(1)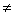 1 1 | x2=0 | 8 | Проверка знака слова В | | 8 | А:=0.0011101 + В:=0.1010010 С:=00.1101111 | Безуслов | 9 | Сложение А и В с занесением в С | | 9 | С(2)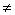 1 1 | x4=0 | 9.2 | Проверка знака слова С | | 9.2 | С(2):=0 | Безуслов | 10 | Присвоение С знака А | | 10 | Конец | | | | | | | | | | 1 | А:=0.0011101 В:=0.1110011 | Безуслов | 2 | Операнды с одинаковыми знаками (положительные) с переполнением | | 2 | П(1):=0 С(1):=0 | Безуслов | 3 | Обнуление | | 3 | А(1)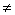 1 1 | x1=0 | 5 | Проверка знака слова А | | 5 | В(1)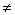 1 1 | x2=0 | 8 | Проверка знака слова В | | 8 | А:=0.0011101 + В:=0.1110011 С:=01.0010000 | Безуслов | 9 | Сложение А и В с занесением в С | | 9 | С(2)=1 | x4=1 | 9.1 | Проверка знака слова С | | 9.1 | П(1):=1 | Безуслов | 10 | Регистрация переполнения | | 10 | Конец | | | | | | | | | | 1 | А:=1.0011101 В:=1.1010010 | Безуслов | 2 | Операнды с одинаковыми знаками (отрицательные) | | 2 | П(1):=0 С(1):=0 | Безуслов | 3 | Обнуление | | 3 | А(1)=1 | x1=1 | 4 | Проверка знака слова А | | 4 | В(1)=1 | x2=1 | 8 | Проверка знака слова В | | 8 | А:=0.0011101 + В:=0.1010010 С:=00.1101111 | Безуслов | 9 | Сложение А и В с занесением в С | | 9 | С(2)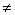 1 1 | x4=0 | 9.2 | Проверка знака слова С | | 9.2 | С(2):=1 | Безуслов | 10 | Регистрация переполнения | | 10 | Конец | | | | | | | | | | 1 | А:=1.0011101 В:=1.1110011 | Безуслов | 2 | Операнды с одинаковыми знаками (отрицательные) с переполнением | | 2 | П(1):=0 С(1):=0 | Безуслов | 3 | Обнуление | | 3 | А(1)=1 | x1=1 | 4 | Проверка знака слова А | | 4 | В(1)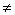 1 1 | x2=0 | 8 | Проверка знака слова В | | 8 | А:=0.0011101 + В:=0.1110011 С:=01.0010000 | Безуслов | 9 | Сложение А и В с занесением в С | | 9 | С(2)=1 | x4=1 | 9.1 | Проверка знака слова С | | 9.1 | П(1):=1 | Безуслов | 10 | Регистрация переполнения | | 10 | Конец | | | |
Продолжение табл. 20
| 1 | 2 | 3 | 4 | 5 | | 1 | А:=1.0011101 В:=0.1010010 | Безуслов | 2 | Операнды с разными знаками | | 2 | П(1):=0 С(1):=0 | Безуслов | 3 | Обнуление | | 3 | А(1)=1 | x1=1 | 4 | Проверка знака слова А | | 4 | В(1)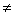 1 1 | x2=0 | 4.1 | Проверка знака слова В | | 4.1 | А:=1.1100010 + В:=0.1010010 С:=10.0110100 | Безуслов | 6 | Сложение инверсии А с В и занесением в С | | 6 | С(1)=1 | x3=1 | 6.1 | Проверка переноса из знакового разряда слова С | | 6.1 | С(1:26):=С(1:26)+1 С=10,0110101 | Безуслов | 7 | Прибавление единицы | | 7 | С(2)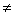 1 1 | x4=0 | 10 | Проверка знака слова С | | 10 | Конец | | | | | | | | | | 1 | А:=0.0011101 В:=1.1010010 | Безуслов | 2 | Операнды с разными знаками | | 2 | П(1):=0 С(1):=0 | Безуслов | 3 | Обнуление | | 3 | А(1)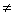 1 1 | x1=0 | 5 | Проверка знака слова А | | 5 | В(1)=1 | x2=1 | 5.1 | Проверка знака слова В | | 5.1 | А:=0.0011101 + В:=1.0101101 С:=01.1001010 | Безуслов | 6 | Сложение инверсии А с В и занесением в С | | 6 | С(1)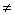 1 1 | x3=0 | 7 | Проверка переноса из знакового разряда слова С | | 7 | С(2)=1 | x4=1 | 7.1 | Проверка знака слова С | | 7.1 | С(1:26):=С(1:2).ùС(3:26) С=01.0110101 | Безуслов | 10 | Инвертирование числовых разрядо (образование прямого кода) | | 10 | Конец | | | |
Страницы: 1, 2
|

|

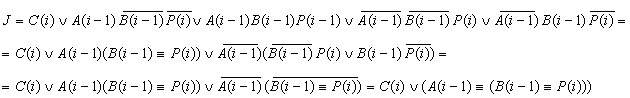
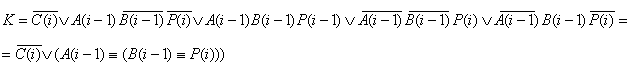
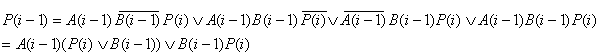 y4:
C(i):=C(i)+P(i)
y4:
C(i):=C(i)+P(i)
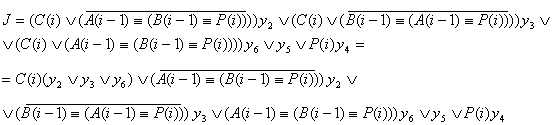
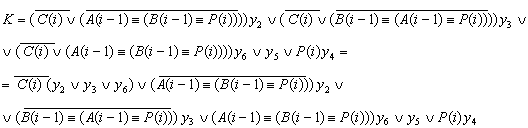
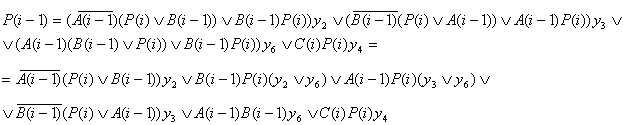
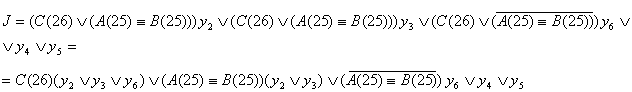
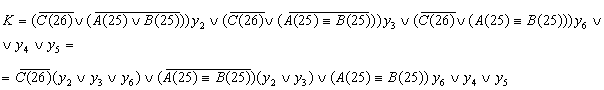
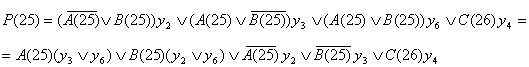
 Рис. 2.2.10.
Рис. 2.2.10.
 Рис. 2.2.11.
Рис. 2.2.11.
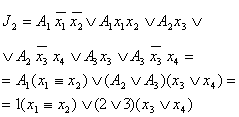
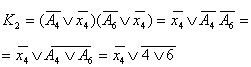 Таблица 18
Таблица 18
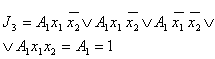
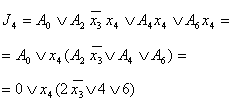
 Функциональная схема управляющего автомата приведена на функциональной схеме
операционного устройства, где показаны связи между операционным и управляющим
автоматами.
4. Функциональная схема операционного устройства
4.1. Организация связи между операционным и управляющим автоматами
Связи между операционным и управляющим автоматами организуются так. Сигналы с
выходов управляющего автомата подаются на его же входы, а также на входы
операционного автомата. На входы управляющего автомата подаются также сигналы
логических условий. Каждая микрооперация выполняется строго при поступлении
синхроимпульса и при подаче соответствующего управляющего сигнала, который в
свою очередь вырабатывается на основе сигналов логических условий,
вычисленных в предыдущий такт работы операционного устройства.
Графически связи между операционным и управляющим автоматами показаны на
функциональной схеме операционного устройства, приведенной на
масштабно–координатной бумаге.
4.2. Описание работы операционного устройства на заданном отрезке времени
Дано:
А=1.1010010
В=0.0011101
После выполнения микрооперации y1 на входы управляющего автомата
приходит сигнал Y1 и сигналы логических условий,
Функциональная схема управляющего автомата приведена на функциональной схеме
операционного устройства, где показаны связи между операционным и управляющим
автоматами.
4. Функциональная схема операционного устройства
4.1. Организация связи между операционным и управляющим автоматами
Связи между операционным и управляющим автоматами организуются так. Сигналы с
выходов управляющего автомата подаются на его же входы, а также на входы
операционного автомата. На входы управляющего автомата подаются также сигналы
логических условий. Каждая микрооперация выполняется строго при поступлении
синхроимпульса и при подаче соответствующего управляющего сигнала, который в
свою очередь вырабатывается на основе сигналов логических условий,
вычисленных в предыдущий такт работы операционного устройства.
Графически связи между операционным и управляющим автоматами показаны на
функциональной схеме операционного устройства, приведенной на
масштабно–координатной бумаге.
4.2. Описание работы операционного устройства на заданном отрезке времени
Дано:
А=1.1010010
В=0.0011101
После выполнения микрооперации y1 на входы управляющего автомата
приходит сигнал Y1 и сигналы логических условий,