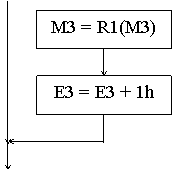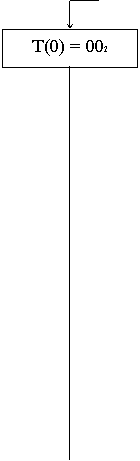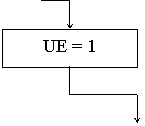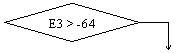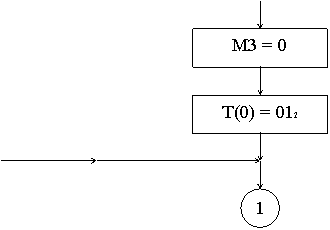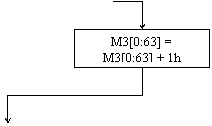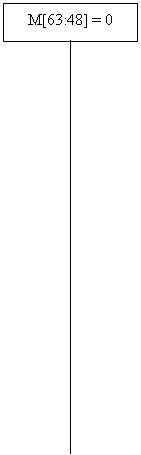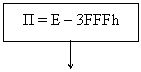|
|
Курсовая: Разработка процессора с плавающей точкой
Курсовая: Разработка процессора с плавающей точкой
Министерство общего и
профессионального образования
Российской Федерации.
Рязанская Государственная
Радиотехническая Академия.
Кафедра ЭВМ.
Пояснительная записка к курсовому проекту
«Разработка процессора с плавающей точкой»
по курсу
«Организация ЭВМ и систем».
Выполнил:
Ст. гр. 143
Бодров В.В.
Проверил:
Доц. каф. ЭВМ
Елесина С.И.
Рязань 2002 г.
Содержание:
Стр.1 – Титульный лист.
Стр.2 – Содержание.
Стр.3 – Задание.
Стр.4 – Форматы данных.
Стр.6 – Программная модель процессора.
Стр.9 – Описание команд.
Стр.11 – Блок-схема процессора.
Стр.12 – Алгоритмы операций.
Стр.21 – Структурные схемы блоков процессора.
Стр.31 – Моделирование операций.
Стр.38 – Заключение.
Стр.38 – Примечания.
Задание
FDiv St(i),St – деление.
Команда деления производит деление стека St(i) на вершину стека и возвращает
частное в получатель.
St(i) ß St(i)/St
Один из операндов находится в регистровом стеке St(i) в формате 80 Real ,
второй в вершине регистрового стека St в формате 80 Real.
Особые случаи: P,U,Z,O,D,I.
FIST m16int – сохранение целочисленное.
Команда сохранения преобразует значение из регистра St в формат получателя и
помещает операнд в ОП. Если получателем является регистр, номер используемого
регистра берётся до извлечения из стека.
m16intß St
Особые случаи: P,I,U,O,D.
Ёмкость ОП 8Кбайт.
Длина слова памяти 32 бита.
I. Форматы данных.
1.1.Внутренний формат.
Во внутренних операциях процессор с плавающей точкой (ППТ) использует
представление вещественных чисел в формате с расширенной точностью РТ
(рис.1.1). Длина формата 80 бит.
14 0 0 63
79 78 64 63 62 0
рис.1.1 Внутренний формат РТ.
Значащие цифры числа находятся в поле мантиссы (M). Длина мантиссы 64 бита.
Поле порядка (Е) показывает фактическое положение двоичной точки в разрядах
мантиссы. Длина порядка 15 бит. Бит знака S определяет знак числа. Мантисса
представлена в прямом коде. Порядок E задаётся в смещённой форме; он равен
истинному порядку (П), увеличенному на значение смещения – смещ. РТ = 16383:
Е = П + смещ РТ.
Истинный порядок изменяется от –16382 до 16383. Смещённые порядки 000..0В и
111..1В зарезервированы для специальных значений. Числа в формате РТ имеют
явный бит F0.
Значение числа в формате РТ равно
S (Е-смещ РТ)
(-1) * 2 * (F0).(F1)(F2).(F63)
Пример:
Число – 15 в формате РТ будет выглядеть следующим образом:
14 0 0 63
| 1 | 01000.00010 | 1. | 1110000000000000000000000000000.000 |
79 78 64 63 62 0
Рис.1.1.а. Пример записи числа в формате РТ.
1.2.Внешние форматы.
В данном курсовом проекте рассматривается один внешний формат: 16int – целое
слово (ЦС) .
Формат ЦС представлен на рис.1.2. Длина формата 16 бит.
15 14 0
Рис.1.2. Формат ЦС.
Бит знака S определяет знак числа. Для представления чисел применяется
стандартный дополнительный код (ДК). Диапазон чисел:
-32768.+ 32767. Все двоичные целые числа точно представимы в формате РТ.
Пример:
Число 5 в формате ЦС будет выглядеть следующим образом:
15 14 0
Рис.1.2.а. Пример записи числа формате ЦС.
II.Программная модель процессора.
Программная модель (рис.2.1) включает в себя кольцевой стек из восьми
регистров R0-R7, регистры слова тэгов TW , слова состояния SW и слова
управления CW. В стеке хранятся числа в формате РТ. Вершина стека
определяется полем ТОР слова состояния SW и обозначается ST(0) или ST. На
рисунке вершиной стека является физический регистр R3. ST(0) содержит
последнее включённое в стек значение, регистр ST(1) предпоследнее и т.д.
Включение в стек осуществляет декремент ТОР и загрузку в новую вершину стека.
При извлечении из стека данное читается из ST(0), а затем производится
декремент ТОР.
15 13 11 0
SW | * | C3 | Т О Р 011 | C2 C1 C0 | Флажки ошибок |
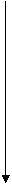 15 0
TW
15 0
TW
| R0 | |  ST(5) ST(5)
| | T(5) | R1 | ST(6) | T(6) | R2 | ST(7) | T(7) |   R3 R3
| Вершина стека ST(0) | T(0) | | R4 | ST(1) | T(1) | | R5 | ST(2) | T(2) | | R6 | ST(3) | T(3) | R7 | ST(4) | T(4) |
79 0
1 0
Рис.2.1. Программная модель процессора.
С каждым регистром стека ассоциируется двухбитный тэг, характеризующий
хранимое число:
00 – нормализованное число;
01 – истинный нуль;
10 – денормализованное число;
11 – пустой регистр.
В слове состояния SW поле ТОР содержит адрес текущей вершины стека. Биты кода
условия C0-C3 фиксируют результаты команд сравнения, проверки и анализа.
Восемь бит отведены для регистрации особых случаев (ошибок) (рис.2.2).
15 14 13 11 10 9 8 7 6 5 4
3 2 1 0
| SW | * | C3 | TOP | | C1 | C0 | ES | SF | PE | UE | OE | ZE | DE | IE |
Рис.2.2. Регистр SW
При выполнении команд с ПТ возможны следующие особые случаи:
- P – неточный результат (точность);
- U – антипереполнение;
- O – переполнение;
- D – денормализованный операнд;
- I – недействительная операция;
- Z – деление на нуль.
Особым случаям соответствуют флажки в слове состояния SW (рис.2.2):
IE,ZE,DE,OE,UE,PE. При любом особом случае устанавливается бит суммарной
ошибки ES, а также вырабатывается активный сигнал ошибки FERR.
В слове управления CW поле RC задаёт режим округления, когда формат получателя
не позволяет точно представить результат. Пусть В - точный результат, А и С –
ближайшие к нему представимые в заданном формате числа: А<В<С. Поле RC
задаёт режим округления:
00 – округление к ближайшему – выбор из А и С, ближайшего к В;
01 – округление вниз – А;
10 – округление вверх – С;
11 – усечение – меньшее из А и С по модулю.
Младшие 6 битов CW хранят маски особых случаев (рис.2.3). Если бит маски
установлен, прерывание при соответствующем особом случае не происходит. Если
бит маски сброшен, происходит прерывание.
15 7 6 5 4
3 2 1 0
Рис.2.3 Маски особых случаев.
В данном курсовом проекте возможны следующие особые случаи: P,U,Z,O,D,I.
Недействительная операция.
Этот случай возникает при антипереполнении стека (попытка извлечения из
пустого регистра). Стековые операции распознаются по биту SF=1 в SW. При
антипереполнении стека бит C1=0. В операции FIST формируется особый случай I
если значение в регистре ST слишком велико для представления целым числом.
Переполнение.
Возникает, когда округлённый результат арифметической команды с
преобразованием формата превышает наибольшее конечное число в формате
получателя.
Денормализованный операнд.
Возникает при попытке оперировать денормализованным операндом.
III.Описание команд.
3.1. FDiv St(i),St – деление.
Команда деления производит деление стека St(i) на вершину стека и возвращает
частное в получатель.
St(i) ß St(i)/St
Один из операндов находится в регистровом стеке St(i) в формате 80 Real ,
второй в вершине регистрового стека St в формате 80 Real.
Особые случаи: P,U,Z,O,D,I.
P – неточный результат(точность);
U – антипереполнение;
Z – деление на нуль;
O – переполнение;
D – денормализованный операнд;
I – недействительная операция;
Формат команды представлен на рис.3.1.
Рис3.1. Формат команды FDiv St(i),St.
Команды данного формата осуществляют операции над вершиной стека и регистром
St(i). Бит R (Reverse) показывает, возвращается ли результат в вершину стека
(R=0) или в St(i) (R=1). Бит P=1 (Pop) указывает, что после операции
производится извлечение из стека.
В данном случае бит R=1 – результат возвращается в St(i).
3.2. FIST m16int – сохранение целочисленное.
Команда сохранения преобразует значение из регистра St в формат получателя и
помещает операнд в ОП. Если получателем является регистр, номер используемого
регистра берётся до извлечения из стека.
m16intß St
Особые случаи: P,I,U,O,D.
P – неточный результат (точность);
I – недействительная операция;
U – антипереполнение;
O – переполнение;
D – денормализованный операнд;
Формат команды представлен на рис.3.2.
| 11011 | MF | 1/0 | | Mod | 1 | КОп | r/m | | Sib | | Disp |
Рис.3.2. Формат команды FIST m16int.
Адрес операнда m16int определяется полями mod, r/m, sib и disp. Адрес
вычисляется целочисленным процессором. К началу операции он уже сформирован.
Бит [0] первого байта команды определяет тип операции. В данном случае бит
[0]=1 – передача данного из стека в память. Поле MF определяет тип операнда.
При m16int MF=11.
IV. Блок-схема процессора.
На основании анализа заданных операций, укрупнённая блок-схема процессора
представлена на рис.4.1. В него входят оперативная память ОП, блок
преобразования форматов БПФ, блок регистров БР, блок обработки данных БОД,
блок микропрограммного управления БМУ. БПФ и ОП связаны 32-битной шиной,
через неё передаются данные из БПФ в ОП в формате 16int. БПФ осуществляет
преобразование из формата РТ в формат ЦС. БР включает в себя регистровый
стек, регистры слов тэгов, управления и состояния. Из БР в БПФ передаётся
операнд из вершины стека в формате РТ (операция FIST). Из БР в БОД передаётся
1-й и 2-й операнд для операции деления (FDiv) в формате РТ и из БОД в БР
передаётся результат операции деления в формате РТ в вершину стека. В БОД
осуществляется операция деления. Управление операциями осуществляется БМУ
путём выборки последовательности микрокодов (МК). Обратная связь от БПФ, БР и
БОД к БМУ обеспечивается через шину осведомительных сигналов ОС.
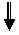 БМУ БМУ
|
 
| Осведомительные сигналы |
Рис.4.1. Блок-схема процессора.
V. Алгоритмы операций.
5.1. Алгоритм операции FDiv St(i),St
Порядок выполнения операции состоит из следующих этапов:
1. Операция деления;
2. Запись результата деления в стек.
1 этап.
Первый операнд читается из стека ST(i) в рабочий регистр RG1:RG1=ST(i).
Второй операнд читается из вершины стека ST в рабочий регистр RG2:RG2=ST.
Частное формируется в RG3.
Регистры операндов RG1 и RG2 и регистр частного RG3 подразделяются на
субрегистры знаков (S1,S2,S3), порядков (E1,E2,E3) и мантисс (M1,M2,M3).
Регистры мантисс расширены до 68 бит для увеличения точности вычислений.
Окончательный результат округляется до 64 бит.
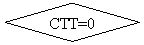
Перед началом деления выявляется случай деления на ноль.
Знак частного S3 = S1 xor S2. Порядок частного E3=E1-E2+16383. Мантисса
частного M3 формируется делением мантиссы делимого M1 на мантиссу делителя
M2. При делении нормализованных чисел 0.10...0 < M3 < 1.11...1.
Если M3<1.0 выполняется нормализация -сдвиг M3 влево на 1 бит и декремент
E3.
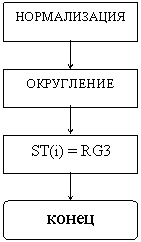
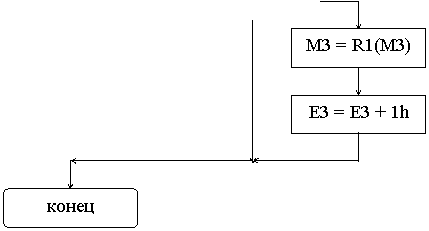
Операция деления FDiv завершается нормализацией и округлением результата:
- если М3 получился в ДК, то М3 преобразуется в прямой код (ПК) М3 = not М3 + 1;
- если произошло переполнение мантиссы, то делаем нормализацию вправо : М3 =
R1(M3), Е3= ЕЗ +1;
- если отсутствует явный бит в М3, то делаем нормализацию влево : М3 =
Lk(M3), Е3= ЕЗ - k, где k - число ведущих нулей;
- округление М3 до 64 бит в зависимости от режима округления - поле RC (табл
5.1).
Округление результата
Таблица 5.1
| RC | режим | г | действие округления | 00 10 | к ближайшему вверх | г< 1000 | отбросить младшие биты | | г=1000 | если младший сохраняемый бит 1 -прибавить к нему 1, отбросить младшие биты | 01 11 | вниз усечение | любое | отбросить младшие биты |
При нормализации возможны следующие особые случаи:
- мантисса М3=0 (потеря значимости);
- при инкременте Е3 возникает переполнение порядка;
- при декременте Е3 возникает антипереполнение порядка.
При возникновении подобных случаев фиксируются следующие признаки результата:
- Z - нулевой результат,
- S - знак результата;
- Р - потеря точности;
- О - переполнение порядка;
- U - антипереполнение порядка.
Маскированные реакции на особые случаи:
- Z - запись в ST(i) истинного нуля;
- О - запись кода бесконечности;
- U - запись кода нуля или денормализованного значения.
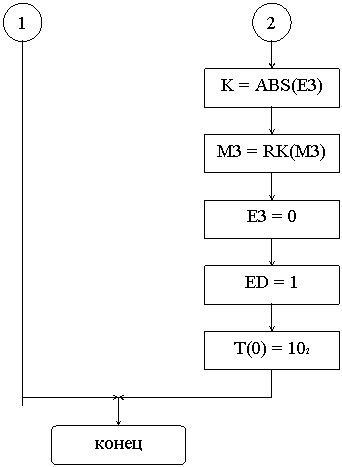
Схема операции FDiv приведена на рис.5.4.
5.2. Алгоритм операции FIST m16int.
Порядок выполнения операции состоит из следующих этапов:
1. Чтение операнда из вершины стека ST в БПФ;
2. Преобразование операнда из формата 80real в формат 16int ;
3. Запись операнда в формате 16int в ОП.
1 этап.
Если регистр ST не пустой T(0) ¹11, то читаем операнд в RGD=ST(0).
Регистр операндов RGD подразделяется на субрегистры знака (S), порядка (E) и
мантиссы(М).
2 этап.
Преобразование начинается с проверки Т(0) регистра слова тэгов TW.
00 – нормализованное число;
01 – истинный ноль;
10 – денормализованное число.
Если число денормализовано, то результат будет нулевым (мантисса меньше
единицы).
Если число нормализовано, то переполнение фиксируется если
П = Е - 16383 >= 15. Если переполнение замаскировано, то в память будет
записано наибольшее (по модулю) отрицательное число.
При отсутствии переполнения мантисса сдвигается вправо на k разрядов M = Rk(M)
,где k = 15 – П. Значение k изменяется от 1 до 14. Если k > 14, то число
равно нулю. Далее производим округление результата (табл. 5.1). Младшие 48 бит
обнуляются M[47:0] = 0. Если число отрицательное , оно преобразуется в ДК: M =
not M + 1.
Преобразованное число находится в 63-48 разрядах (рис 5.2).
RGD
79 64 63 62
48 47 0
Рис. 5.2. Расположение преобразованного числа в RGD.
Позиционирование данных в RGRW зависит от положения числа в RGD и младших
битов адреса EAR[0:1] (табл. 5.3).
Размещение данных в RGRW. Таблица 5.3.
| EAR[0:1] | 00 | 01 | | Разряды RGRW | 15:0 | 31:16 |
CASE EAR[0:1]
00: RGRW[15:0] = R47(RGD)
01: RGRW[31:16] = R31(RGD)
EAR[0:1] = 10 и EAR[0:1] = 11 – запрещены.
Алгоритм операции Fist m16int приведён на рис. 5.5.
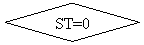 1 1
 0 0
   0 1
0 1
 0 0
 1
Рис. 5.4. FDiv St(i),St. 1
Рис. 5.4. FDiv St(i),St.
 1 1
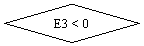 1 1
 1
1
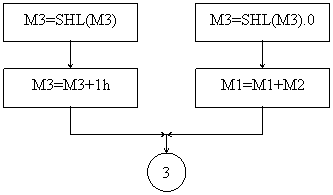
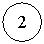  Рис.5.4.а. Нормализация.
Рис.5.4.а. Нормализация.
 1 1
 ![Блок-схема: решение: M3[64]](/image/21594_51_1.gif) 0 0
![Блок-схема: решение: M3[0]](/image/21594_54_1.gif) 1
Рис.5.4.б. Округление.
1
Рис.5.4.б. Округление.
 Рис. 5.5 Алгоритм операции
Fist m 16int.
Рис. 5.5 Алгоритм операции
Fist m 16int.
 0 0
 1 1
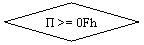 0 1 0 1
 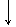 1 1
 1 1
Страницы: 1, 2, 3
|

|

 1
1
 Рис. 5.5 Алгоритм операции
Рис. 5.5 Алгоритм операции