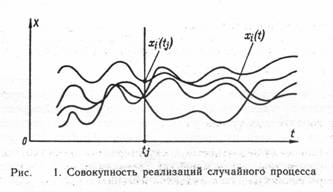
Реферат: Измерение случайных процессов

Реферат: Измерение случайных процессов

Реферат на тему : Измерение случайных процессов.

Содержание

1. Общие сведения об измерениях. . . . . . . . . . . .

. . . . . . . стр 3.

2. Измерения математического ожидания и дисперсии

случайного процесса. . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . стр 9.

3. Измерение функций распределения вероятности. . . .

стр 11.

4. Измерения корреляционной функции. . . . . . . . . .

. . . . стр 13.

5. Анализ спектра мощности. . . . . . . . . . . . . . .

. . . . . . . . стр 14.

6. Приложения . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . стр 16.

7. Список литературы. . . . . . . . . . . . . . . . . .

. . . . . . . . . . . стр 17.

ИЗМЕРЕНИЯ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ

1. ОБЩИЕ СВЕДЕНИЯ

Измерения вероятностных характеристик случайных процес­сов (статистические

измерения) составляют один из наиболее быстро развивающихся разделов

измерительной техники. В на­стоящее время область распространения

статистических методов исследования и обработки сигналов измерительной

информации практически безгранична. Связь, навигация, управление,

диагно­стика (техническая, медицинская), исследование среды и многие другие

области немыслимы без знания и использования свойств сигналов и помех,

описываемых их вероятностными характери­стиками.

Потребность в изучении свойств случайных процессов приве­ла к развитию

соответствующих методов и средств (преимуще­ственно электрических). Появление

анализаторов функций рас­пределения вероятностей, коррелометров, измерителей

математи­ческого ожидания, дисперсиометров и других видов измерителей

вероятностных характеристик открыло новые возможности в об­ласти создания

современной информационной и управляющей техники.

Рассмотрим необходимые исходные определения и общие сведения о статистических

измерениях.

В теории статистических измерений используют следующие понятия и их аналоги,

заимствованные из теории случайных функций (аналоги из математической

статистики): реализация случайного процесса (выборочная функция), мгновенное

значе­ние (выборочное значение), совокупность мгновенных значений (выборка),

вероятностная характеристика (предел выборочного среднего).

Введем следующие обозначения: Х (t) — случайный процесс;

i-порядковый номер реализации случайного процесса Х (t);

xi(tj) —мгновенное значение процесса Х (t), соответствующее

значению (i-й реализации в j-й момент времени. Случайным

назы­вают процесс Х (t), мгновенные значения которого xi (tj)

суть случайные величины.

На рис.1 представлена в качестве примера совокупность реализации случайного

процесса, воспроизводящих зависимости некоторого параметра Х от времени

t.

В теории случайных процессов их полное описание произво­дится с помощью

систем вероятностных характеристик: многомерных функций распределения

вероятности, моментных функ­ций, характеристических функций и т. п. В теории

статистиче­ских измерений исследуемый случайный процесс представляется своими

реализациями, причем полное представление осуществля­ется с помощью так

называемого ансамбля, т. е. бесконечной совокупностью реализаций. Ансамбль —

математическая аб­стракция, модель рассматриваемого процесса, но конкретные

реализации, используемые в измерительном эксперименте, пред­ставляют собой

физические объекты или явления и входят в ан­самбль как его неотъемлемая

часть.

Если случайный процесс представлен ансамблем реализации xi (t), i=1, 2,

..., со, то вероятностная характеристика в может быть определена усреднением по

совокупности, т.е.

N

q [X (t)]=lim 1/N S g[xi(t)], (1)

N® ¥ i =1

где g [Xi (t)]— некоторое преобразование, лежащее в основе

оп­ределения вероятностной характеристики q. Так, например, при определении

дисперсии g [Xi (t)]= xi (t). При этом полагаем, что процесс

характеризуется нулевым математическим ожиданием.

Вместо усреднения по совокупности может быть использовано усреднение по времени

с использованием k-й реализации xk (t) и тогда

T

q [X(t)]= lim 1/T ò g[xi(t)]dt. (2)

T ® ¥ 0

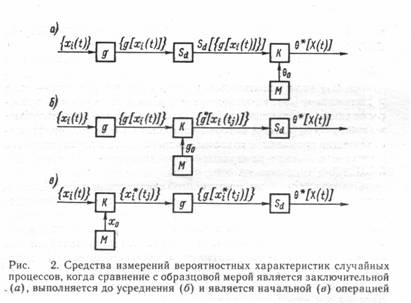
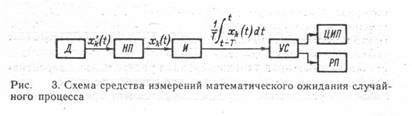
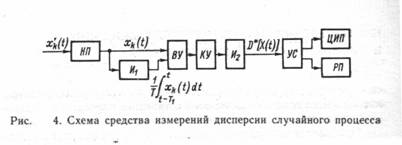
Например, при определении математического ожидания

T

M [X (t)]= lim 1/T ò xk (t) dt. (3)

T® ¥ 0

В общем случае результаты усреднения по совокупности (1) и по времени

(2) неодинаковы. Предел выборочного среднего по совокупности (1)

представляет собой вероятност­ную характеристику, выражающую зависимость

вероятностных свойств процесса от текущего времени. Предел выборочного среднего

по времени (2) представляет собой вероятностную характеристику,

выражающую зависимость вероятностных свойств процесса от номера реализации.

Наличие и отсутствие зависимости вероятностных характери­стик от времени или от

номера реализации определяет такие фундаментальные свойства процесса, как

стационарность и эрго­дичность. Стационарным, называется процесс,

вероятностные ха­рактеристики которого не зависят от времени; соответственно

эргодическим называется процесс, вероятностные характеристи­ки которого не

зависят от номера реализации.

Следовательно, стационарный неэргодический случайный процесс — это такой

процесс, у которого эквивалентны времен­ные сечения (вероятностные

характеристики не зависят от теку­щего времени), но не эквивалентны реализации

(вероятностные характеристики зависят от номера реализации).

Нестационар­ный эргодический процесс — это процесс, у которого эквивалент­ны

реализации (вероятностные характеристики не зависят от номера реализации), но

не эквивалентны временные сечения (вероятностные характеристики зависят от

текущего времени). Классифицируя случайные процессы на основе этих призна­ков

(стационарность и эргодичность), получаем следующие четы­ре класса процессов:

стационарные эргодические, стационарные неэргодические, нестационарные

эргодические, нестационарные неэргодические.

Учет и использование описанных свойств случайных процес­сов играет большую

роль при планировании эксперимента по определению их вероятностных

характеристик.

Поскольку измерение представляет собой процедуру нахож­дения величины опытным

путем с помощью специальных техни­ческих средств, реализующих алгоритм,

включающий в себя операцию сравнения с известной величиной, в статических

изме­рениях должна применяться мера, воспроизводящая известную величину.

Типовые алгоритмы измерений вероятностных характеристик случайных процессов,

различающиеся способом применения ме­ры в процессе измерений, представляются

в следующем виде:

q* [X (t)]= KSdg [X (t)]; (4)

q* [X (t)]= Sd Kg [X (t)]; (5)

q* [X (t)]= Sd gK [X (t)]; (6)

где Sd—оператор усреднения; К—оператор сравнения;

q* [X (t)]—результат измерения характеристики q [X (t)].

Данные алгоритмы различаются порядком выполнения опе­раций. Операция сравнения с

образцовой мерой (К) может быть заключительной [см. (4)], выполняться

после реализации оператора g, но до усреднения [см. (5)] и, наконец,

быть началь­ной [см. (6)]. Соответствующие обобщенные структурные схе­мы

средств измерений значений вероятностных характеристик представлены на рис.

2.

На этих рисунках для обозначения блоков, реализующих операторы, входящие в

выражения (4) — (6), используют­ся те же обозначения. Так, g —

устройство, выполняющее пре­образование, лежащее в основе определения

вероятностной ха­рактеристики q; Sd — устройство усреднения (сумматор

или ин­тегратор); К— компаратор (сравнивающее устройство), а М—

мера, с помощью которой формируется известная величина (q., g., x.)

Представленное на рис. 2, а средство измерений реализует

следующую процедуру: на вход поступает совокупность реализа­ций {xi (t)}

(при использовании усреднения по времени — одна реализация xi, (t)

-, на выходе узла g имеем совокупность преоб­разованных реализации {g[xi

(t)]}; после усреднения получаем величину Sd {g[xi (t

)]}, которая поступает на компаратор, осуще­ствляющий сравнение с известной

величиной qо, в результате чего получаем значение измеряемой вероятностной

характеристики q*[X(t)].

Отличие процедуры, реализуемой средством измерений, пред­ставленным на рис.

2, б, заключается в том, что после формиро­вания совокупности {g [xi

(t)]} она поступает не на усреднитель, а на компаратор, который выполняет

сравнение с известной вели­чиной go; на выходе компаратора формируется

числовой массив {g* [xi (ti)]} и усреднение выполняется в числовой

форме. На выхо­де усреднителя Sd имеем результат измерения q* [X

(t)].

Средство измерений (рис. 2, в) основано на формировании массива числовых

эквивалентов мгновенных значений реализа­ции случайного процесса Х (t),

после чего преобразование g и ус­реднение выполняются в числовой форме. Это

устройство эквива­лентно последовательному соединению аналого-цифрового

пре­образователя (АЦП) и вычислительного устройства (процессо­ра). На выходе

АЦП формируется массив мгновенных значений, а процессор по определенной

программе обеспечивает реализа­цию операторов g и Sd,

Погрешность результата измерения вероятностной характе­ристики случайного

процесса

Dq* [X(t)]= q*[X(t)]- q [ X(t)]. (7)

Для статистических измерений характерно обязательное на­личие составляющей

методической погрешности, обусловленной конечностью объема выборочных данных о

мгновенных значени­ях реализации случайного процесса, ибо при проведении

физиче­ского эксперимента принципиально не может быть использован бесконечный

ансамбль реализации или бесконечный временной интервал. Соотношение (7)

определяет результирующую по­грешность, включающую в себя как методическую, так

и инстру­ментальную составляющие. В дальнейшем будут приводиться соотношения

только для определения специфической для стати­стических измерений методической

погрешности, обусловленной конечностью числа реализации и временного интервала.

2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ИДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА

Математическое ожидание и дисперсия случайного процес­са — основные числовые

вероятностные характеристики, измере­ние которых играет большую роль в

практике научных исследова­ний, управления технологическими процессами и

испытаний.

При измерении математического ожидания результатом из­мерения является среднее

по времени или по совокупности мгно­венных значений реализации исследуемого

случайного процесса. Усреднение по времени применяется на практике существенно

чаще, чем усреднение по совокупности, поскольку работать с од­ной реализацией

удобнее и проще, чем с совокупностью. На рис. 3 приведена структурная

схема устройства, реали­зующего алгоритм

t

M* [X (t)]= 1/T ò xk (t) dt.

t-T

На рисунке Д—преобразователь измеряемой величины в электрический сигнал

(датчик); НП — нормирующий преобра­зователь, превращающий входной

сигнал в стандартный по виду и диапазону значений; И — интегратор; УС —

устройство сопря­жения, обеспечивающее согласование выхода интегратора со

входами цифрового вольтметра и регистрирующего прибора;

ЦИП — цифровой прибор (например, цифровой вольтметр);

РП—регистрирующий прибор (самопишущий прибор).

Для оценки среднего квадратичeского значения погрешности, обусловленной

конечностью объема выборочных данных,

можно пользоваться следующими соотношениями:

1/2

s =[2D[X(t)] t k/T]

M°

при усреднении по времени T и

1/2

s =[D[X(t)]/N]

M°

при усреднении по совокупности N. Здесь D[X

(t)]—дисперсия процесса X(t), а t k — интервал корреляции.

Дисперсия случайного процесса характеризует математиче­ское ожидание квадрата

отклонений мгновенных значений реали­зации случайного процесса от

математического ожидания. Таким образом,

T 2

D[X(t)]= lim 1/T ò [xk (t)-[X(t)]] dt

T®¥ 0

или

N 2

D[X(t)]= lim 1/N S [xi(t)-[X(t)]] dt

N®¥ i=1

Возможны различные варианты построения устройств для измерения дисперсии

случайного процесса — дисперсиометров. На рис. 4 приведена структурная

схема средства измерений дисперсии случайного процесса, т. е. работающего

согласно вы­ражению

t t 2

D* [X(t)]=1/T ò [xk (t)- 1/T1 ò xk (t)dt] dt

t-T t-T1

На рисунке НП — нормирующий преобразователь; И1 и И2 —

интеграторы; ВУ— вычитающее устройство; КУ— квадратирующее

устройство; УС — устройство сопряжения; ЦИП — цифро­вой прибор;

РП — регистрирующий прибор.

Средняя квадратическая погрешность из-за конечности объема выборочных данных о

мгновенных значениях Х (t) может быть определена с помощью соотношений

2 1/2

s =[2D[X (t)] t k/T]

M°

, где D[X2 (t)]— дисперсия Х (t); T—время усред­нения.

При усреднении по совокупности N реализаций

2 1/2

s =[D[X (t)] /N]

D°

3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

Одномерная интегральная функция распределения вероятно­сти F (X) равна

вероятности того, что мгновенное значение про­извольной реализации в

произвольный момент времени меньше установленного уровня, т. е. Xi (ti)

£ X. Функция F (X) определя­ется как предел выборочного

среднего:

F (X)= lim Sd [j [x (t) ,X]],

d®¥

1 при x (t) £ X

Где j[x(t) ,X]=

0 при x (t) > X

Поскольку интегральные F (X) и дифференциальные w (X) функции

распределения вероятности связаны между собой со­отношениями

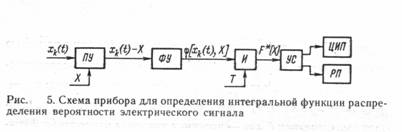
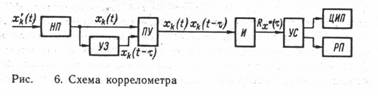
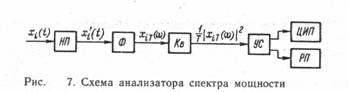
X

w (X) =(dF (X))/dX ; F (X)= ò w (X) dX

-¥

справедливо выражение

w (X) = lim ((F(X+ DX)-F (X))/ DX)= lim ((Sd [Dj[x(t) ,X]])/ DX)

DX®0 DX®0

1 при X < x (t) £ X+ DX

где Dj [x(t) ,X]=

0 при x (t) £ X, x (t) > X+ DX

В качестве примера рассмотрим средство измерений для определения интегральной

функции распределения вероятности уровня электрического сигнала. Схема

средства измерений, реа­лизующего алгоритм

t

F* (X)=1/T ò j [xk(t) ,X]dt ,

t-T

показана на рис. 5, где ПУ — пороговое устройство, формиру­ющее

сигнал X k (t}—X; ФУ—формирующее устройство; И—интегратор, на

выходе которого получается сигнал F* (X) при установленных значениях Х

и Т; УС — устройство сопряжения;

ЦИП — цифровой прибор; РП — регистрирующий прибор.

Средняя квадратическая погрешность из-за конечности объема выборки определяется

для F {X) с помощью соотношения

2 1/2

s =[2(F - F ) t k/T]

F°

при усреднении по времени и с помощью соотношения

2 1/2

s =[2(F - F )/N]

F°

при усреднении по совокупно­сти. Для (X) соответствующие

соотношения имеют вид:

2 1/2

s =[2(w - w DX) t k/T]

w°

2 1/2

и s =[(w - w DX)/N]

w°

В приведенных соотношениях F и w — истинные значения измеряемых функ­ций

при данном X.

4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ

Для случайного процесса с нулевым математическим ожида­нием корреляционная

функция равна:

Rx (s, t) = lim Sd[xi (t) xi-s (t- t)],

d ®¥

где t и s — соответственно сдвиг во времени и в пространстве реализации

перемножаемых мгновенных значений.

В практических задачах большую роль играют стационарные случайные процессы,

т. е. процессы с постоянными вероятностны­ми характеристиками, не зависящими

от текущего времени. Сре­ди случайных процессов можно выделить эргодические

процессы, для которых

t

Rx (t) = lim 1/T ò x (t) x (t-t)dt,

T ®¥ 0

Большое значение корреляционного анализа в различных областях науки и техники

привело к созданию множества измери­тельных приборов для измерений

корреляционных функций — коррелометров.

Типовая структура коррелометра, в котором используется усреднение по времени,

представлена на рис. 6. При этом реализуется следующий алгоритм:

t

R*x (t) = 1/T ò xk (t) xk (t-t)dt,

t-T

Как видно, после нормирующего преобразователя НП сигнал поступает в

устройство временной задержки УЗ и на перемножа­ющее устройство ПУ,

осуществляющее перемножение мгновен­ных значений, сдвинутых по времени на

интервал т. Далее с по­мощью интегратора И выполняется усреднение,

после которого результирующий сигнал через УС подается на цифровой прибор

ЦИП или регистрирующий прибор РП.

Средние квадратические погрешности, обусловленные ко­нечностью объема выборочных

данных о мгновенных значениях реализации процесса Х (t), оцениваются с

помощью соотноше­ний:

1/2

s ={2D[xk (t) xk (t-t)] t k/T}

R°

при усреднении по времени Т и

1/2

s ={D[xk (t) xk (t-t)]/N}

R°

при усреднении по совокупности.

5. АНАЛИЗ СПЕКТРА МОЩНОСТИ

Спектр мощности характеризует ее частотное распределение, и он может быть

определен в соответствии со следующими форму­лами:

2

Sx(w) = lim 1/T | xiT (w) |

T ®¥

Где

t -jwt’

XiT (w) = ò xi (t’) e dt’

t-T

На рис. 7 изображена схема анализатора спектра мощно­сти случайного

процесса Х (t).

С выхода нормирующего преобразователя НП i-я реализация случайного

процесса xi (t) поступает на блок Ф, выполняющий преобразование Фурье,

после чего узлом Кв производится возве­дение в квадрат и нормирование с

учетом интервала усреднения Т. С помощью устройства сопряжения УС

сформированный сиг­нал поступает на ЦИП и регистратор РП.

В настоящее время отечественной промышленностью серийно выпускаются

анализаторы случайных процессов. К ним относят­ся многофункциональный

статистический преобразователь Ф790, корреллометр Ф7016, комплекс измерителей

характеристик случайных сигналов Х6-4/а, многофункциональные измерители

ве­роятностных характеристик Ф36 и Ф37, анализаторы спектра Ф4326, Ф4327,

Ф7058 и др. С помощью этих приборов и устройств можно измерять математические

ожидания и дисперсии, а также значения функций распределения вероятности,

корреляционных и спектральных функций с последующим восстановлением вида

самих функций. Перечисленные анализаторы рассчитаны в ос­новном на

унифицированный входной сигнал и позволяют изме­рить от 256 до 4096 ординат

анализируемой функции. Погреш­ность измерения не превышает ±5 %.

Кроме того, для определения вероятностных характеристик случайных сигналов

могут использоваться электроизмеритель­ные приборы, предназначенные для

измерения среднего и дей­ствующего значений сигнала. Для определения среднего

значе­ния применяют магнитоэлектрические приборы и цифровые ин­тегрирующие

приборы. Для определения среднего квадратического отклонения используют

приборы, показания которых определяются действующим значением сигнала

(термоэлектри­ческие, электростатические и др.).

Корреляционные устройства получили применение в различ­ных областях науки и

техники для измерения различных величин. В качестве примера можно указать

корреляционное устройство для измерения скорости прокатки. Эти устройства

измеряют кор­реляционную функцию, зависящую от т, которая, в свою очередь,

зависит от скорости прокатки.

Список литературы :

1.Метрология и электроизмерительные приборы. Душин М .Е.\М.:

Энергоатомиздат,1986.

2.Метрология, стандартизация и измерения в технике связи. Под ред. Б.П. Хромого

М.: Радио и связь, 1986.

3.Основы метрологии и стандартизации. Голубева В. П. \М .: Вектор, 1996.