|
|
Диплом: Аналогии в курсе физики средней школы
Диплом: Аналогии в курсе физики средней школы
Выпускная квалификационная работа
''АНАЛОГИИ В КУРСЕ ФИЗИКИ СРЕДНЕЙ ШКОЛЫ''
СОДЕРЖАНИЕ
Введение.......................................................................3
ГЛАВА 1. Электромеханические аналогии
§1. Электромагнитные и механические колебания..................................5
§2. Решение уравнений, описывающих свободные колебания........................15
§3. Решение физических задач..................................................18
§4. Изучение волновых процессов ..............................................25
ГЛАВА 2. Другие виды аналогий в школьном курсе физики
§5.Использование аналогии при изучении транзистора............................32
§6. Изучение электрических цепей с использованием аналогии....................35
§7. Аналогии при изучении постулатов Бора.....................................45
ГЛАВА 3. Изучение аналогий на факультативах, кружках и спецкурсах.
§8. Волчок и магнит...........................................................52
§9. Свет и глаз...............................................................62
Заключение....................................................................70
Список литературы.............................................................71
Введение.
Аналогия - один из методов научного познания, который широко применяется при
изучении физики.
В основе аналогии лежит сравнение. Если обнаруживается, что два или более
объектов имеют сходные признаки, то делается вывод и о сходстве некоторых
других признаков. Вывод по аналогии может быть как истинным, так и ложным,
поэтому он требует экспериментальной проверки.
Значение аналогий при обучении связано с повышением научно-теоретического
уровня изложения материала на уроках физики в средней школе, с формированием
научного мировоззрения учащихся.
В практике обучение аналогии используется в основном для пояснения уже
введенных трудных понятий и закономерностей.
Электромагнитные колебания и волны - темы школьного курса физики, усвоение
которых традиционно вызывает большие затруднения у учащихся. Поэтому для
облегчения изучения электромагнитных процессов используются
электромеханические аналогии, поскольку колебания и волны различной природы
подчиняются общим закономерностям.
Аналогии между механическими и электрическими колебательными процессами с
успехом используются в современных исследованиях и расчетах. При расчете
сложных математических систем часто прибегают к электромеханической аналогии,
моделируя механическую систему соответствующей электрической.
Демонстрационный эксперимент при изучении переменного тока вскрывает лишь
некоторые основные особенности процессов протекания тока по различным
электрическим цепям. Здесь большое значение имеют аналогии, дающие
возможность понять ряд явлений в цепях переменного тока, сущность которых
трудно разъяснить в средней школе другими средствами. К таким вопросам в
первую очередь относятся явления в цепях переменного тока с емкостью и
индуктивностью, а также сдвиг фаз между током и напряжением.
Использование метода аналогии при решении задач может идти в двух направлениях:
1) непосредственное применение этого метода;
2) отыскание физической системы, которая аналогична данной в условии задачи.
В данной работе будут рассмотрены следующие аналогии, изучаемые в курсе
физики средней школы: электромагнитные и механические колебания; решение
уравнений, описывающих колебания в пружинном и математическом маятниках;
решение физических задач; изучение волновых процессов; изучение электрических
цепей с использованием аналогии; использование аналогии при изучении
транзистора; аналогии при изучении постулатов Бора; волчок и магнит; свет и
глаз.
Таким образом аналогии позволяют учащимся более глубоко понять известные
физические явления, понятия и процессы.
ГЛАВА 1 ЭЛЕКТРОМЕХАНИЧЕСКИЕ АНАЛОГИИ.
§ 1 Электромагнитные и механические аналогии.
В теме " Электромагнитные колебания " рассматривается электромагнитный
процесс, возникающий при разрядке конденсатора через катушку индуктивности и
делается вывод о колебательном характере этого процесса.
Электромагнитные колебания в контуре имеют сходство со свободными
механическими колебаниями, например с колебаниями тела, закрепленного на
пружине. Сходство относится не к природе самих величин, которые периодически
изменяются, а к процессам периодического изменения различных величин.
При механических колебаниях периодически изменяются координата тела x и проекции
его скорости 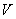 , а
при электромагнитных колебаниях меняются заряд конденсатора q и сила тока в
цепи i. Одинаковый характер изменения величин (механических и электрических)
объясняется тем, что имеется аналогия в условиях, при которых порождаются
механические и электромагнитные колебания. Возвращение к положению равновесия
тела на пружине вызывается силой упругости F , пропорциональной смещению тела
от положения равновесия. Коэффициентом пропорциональности является жесткость
пружины k. Разрядка конденсатора (появление тока) обусловлена напряжением U
между пластинами конденсатора, которое пропорционально заряду q. Коэффициентом
пропорциональности является величина , а
при электромагнитных колебаниях меняются заряд конденсатора q и сила тока в
цепи i. Одинаковый характер изменения величин (механических и электрических)
объясняется тем, что имеется аналогия в условиях, при которых порождаются
механические и электромагнитные колебания. Возвращение к положению равновесия
тела на пружине вызывается силой упругости F , пропорциональной смещению тела
от положения равновесия. Коэффициентом пропорциональности является жесткость
пружины k. Разрядка конденсатора (появление тока) обусловлена напряжением U
между пластинами конденсатора, которое пропорционально заряду q. Коэффициентом
пропорциональности является величина 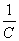 , обратная емкости, так как
, обратная емкости, так как 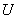 =
=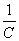 q.
Подобно тому как вследствии инертности тело лишь постепенно увеличивает скорость
под действием силы и эта скорость после прекращения действия силы не становится
сразу равной нулю, электрический ток в катушке за счет явления самоиндукции
увеличивается под действием напряжения постепенно и не исчезает сразу, когда
это напряжение становится равным нулю. Индуктивность контура L играет туже
роль, что и масса тела m в механике. Соответственно кинетической энергии тела q.
Подобно тому как вследствии инертности тело лишь постепенно увеличивает скорость
под действием силы и эта скорость после прекращения действия силы не становится
сразу равной нулю, электрический ток в катушке за счет явления самоиндукции
увеличивается под действием напряжения постепенно и не исчезает сразу, когда
это напряжение становится равным нулю. Индуктивность контура L играет туже
роль, что и масса тела m в механике. Соответственно кинетической энергии тела 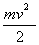 отвечает энергия магнитного поля тока
отвечает энергия магнитного поля тока 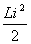 , а импульсу тела mv отвечает поток магнитной индукции Li .
Зарядке конденсатора от батареи соответствует сообщение телу, прикрепленному к
пружине, потенциальной энергии
, а импульсу тела mv отвечает поток магнитной индукции Li .
Зарядке конденсатора от батареи соответствует сообщение телу, прикрепленному к
пружине, потенциальной энергии 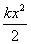 при смещении тела на расстояние
при смещении тела на расстояние 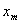 от положения равновесия (рис. 1,а).
Сравнивая это выражение с энергией конденсатора
от положения равновесия (рис. 1,а).
Сравнивая это выражение с энергией конденсатора 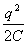 , замечаем, что жесткость k пружины играет при механическом колебательном
процессе такую же роль, как величина
, замечаем, что жесткость k пружины играет при механическом колебательном
процессе такую же роль, как величина 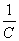 , обратная емкости, при электромагнитных колебаниях, а начальная координата
, обратная емкости, при электромагнитных колебаниях, а начальная координата 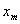 соответствует заряду
соответствует заряду 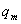 .
Возникновение в электрической цепи тока i за счет разности потенциалов
соответствующих появлению в механической колебательной системе скорости
.
Возникновение в электрической цепи тока i за счет разности потенциалов
соответствующих появлению в механической колебательной системе скорости 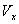 под действием силы упругости пружины (рис.1,б). Моменту, когда конденсатор
разрядится, а сила тока достигнет максимума, соответствует прохождение тела
через положение равновесия с максимальной скоростью (рис.1.в). Далее
конденсатор начнет перезаряжаться, а тело смещаться влево от положения
равновесия (рис.1,г). По прошествии половины периода Т конденсатор полностью
перезарядится и сила тока станет равной нулю. Этому состоянию соответствует
отклонение тела в крайнее левое положение, когда его скорость равна нулю
(рис.1,д).
Рассмотренные выше колебания являются свободными. Здесь не учтено, что в
любой реальной механической системе существуют силы трения.
Таким образом, соответствие между механическими и электрическими величинами
при колебательных процессах можно представить в виде таблицы 1
под действием силы упругости пружины (рис.1,б). Моменту, когда конденсатор
разрядится, а сила тока достигнет максимума, соответствует прохождение тела
через положение равновесия с максимальной скоростью (рис.1.в). Далее
конденсатор начнет перезаряжаться, а тело смещаться влево от положения
равновесия (рис.1,г). По прошествии половины периода Т конденсатор полностью
перезарядится и сила тока станет равной нулю. Этому состоянию соответствует
отклонение тела в крайнее левое положение, когда его скорость равна нулю
(рис.1,д).
Рассмотренные выше колебания являются свободными. Здесь не учтено, что в
любой реальной механической системе существуют силы трения.
Таким образом, соответствие между механическими и электрическими величинами
при колебательных процессах можно представить в виде таблицы 1
Механические величины | Электрические величины | | Координата х | Заряд q | Скорость vx=x' | Сила тока i=q' | Ускорение аx=vx | Скорость изменения силы тока i' | Масса m | Индуктивность L | | Жесткость k | Величина, обратная электроемкости. 1/С | | Сила F | Напряжение U | | Вязкость b | Сопротивление R | Потенциальная энергия деформированной пружины kx2/2 | Энергия электрического поля конденсатора q2/(2C) | Кинетическая энергия mv2/2 | Энергия магнитного поля катушки Li2/2 | Импульс mv | Поток магнитной индукции Li |
Выведем уравнение свободных незатухающих электромагнитных колебаний в контуре и
колебаний горизонтального пружинного маятника. Применяя к пружинному маятнику
закон сохранения энергии, получим равенство: 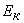 +
+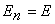 , где , где
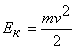 , , 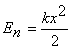 , тогда имеем , тогда имеем
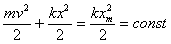 (1)
Так как (1)
Так как
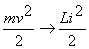 и и 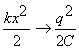 получаем получаем
 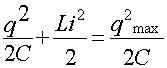 =const (2)
Следует заметить, что уравнение (2) так же следует из закона сохранения энергии.
В уравнении (2) i=q' - мгновенное значение силы тока, qmax
- максимальный заряд на конденсаторе (он не должен вызвать пробоя). Делаем
вывод о зависимости силы тока от величины заряда и находим значение
максимальной силы тока: =const (2)
Следует заметить, что уравнение (2) так же следует из закона сохранения энергии.
В уравнении (2) i=q' - мгновенное значение силы тока, qmax
- максимальный заряд на конденсаторе (он не должен вызвать пробоя). Делаем
вывод о зависимости силы тока от величины заряда и находим значение
максимальной силы тока:
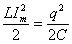 ; ; 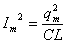 Откуда Откуда
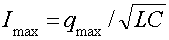 при q=0.
Как видно формально с точки зрения математики уравнения (1) и (2) являются
одинаковыми.
Решаем уравнение (2): производная полной энергии по времени равна нулю, так
как энергия постоянна.
Следовательно, равна нулю сумма производных по времени от энергий магнитного
и электрического полей. при q=0.
Как видно формально с точки зрения математики уравнения (1) и (2) являются
одинаковыми.
Решаем уравнение (2): производная полной энергии по времени равна нулю, так
как энергия постоянна.
Следовательно, равна нулю сумма производных по времени от энергий магнитного
и электрического полей.
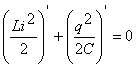 или или
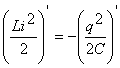 (3) (3)
 Физический смысл уравнения (3) состоит в том, что скорость изменения энергии
магнитного поля по модулю равна скорости изменения энергии электрического
поля; знак “минус” указывает на то, что, когда энергия электрического поля
возрастает, энергия магнитного поля убывает (и наоборот). Поэтому полная
энергия не меняется.
Вычисляя обе производные получаем:
Физический смысл уравнения (3) состоит в том, что скорость изменения энергии
магнитного поля по модулю равна скорости изменения энергии электрического
поля; знак “минус” указывает на то, что, когда энергия электрического поля
возрастает, энергия магнитного поля убывает (и наоборот). Поэтому полная
энергия не меняется.
Вычисляя обе производные получаем:
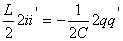
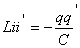 так как
так как 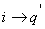 , тогда , тогда
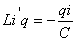 и и 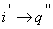 получаем
получаем
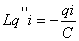
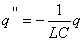 (4)
Уравнение (4) является основным уравнением, описывающем процессы в
колебательном контуре.
Рассмотрим колебания вертикального пружинного и математического маятников. (4)
Уравнение (4) является основным уравнением, описывающем процессы в
колебательном контуре.
Рассмотрим колебания вертикального пружинного и математического маятников.
 Выведем груз из
положения равновесия, растянув пружину на длину Хm (рис.2) и
отпустим. (Амплитудное растяжение пружины Xm должно быть
таково, чтобы был справедлив закон Гука Выведем груз из
положения равновесия, растянув пружину на длину Хm (рис.2) и
отпустим. (Амплитудное растяжение пружины Xm должно быть
таково, чтобы был справедлив закон Гука 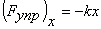 и выводимая на его основе формула потенциальной энергии пружины.)
и выводимая на его основе формула потенциальной энергии пружины.)
 Рис.2 Рис.2

 Мгновенные значения
координаты груза х в процессе колебаний лежат в пределах -xm
£x£xm . По закону сохраненья энергии имеем: Мгновенные значения
координаты груза х в процессе колебаний лежат в пределах -xm
£x£xm . По закону сохраненья энергии имеем:

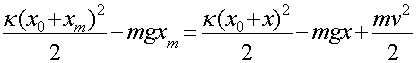 (5)
где X0=mg/k - статическое растяжение пружины (потенциальную
энергию груза в поле силы тяжести отсчитываем от уровня равновесия груза,
обозначенного на рис. 2 пунктиром). Учитывая, что
(5)
где X0=mg/k - статическое растяжение пружины (потенциальную
энергию груза в поле силы тяжести отсчитываем от уровня равновесия груза,
обозначенного на рис. 2 пунктиром). Учитывая, что 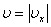 и
и 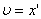 , получим
уравнение колебаний , получим
уравнение колебаний
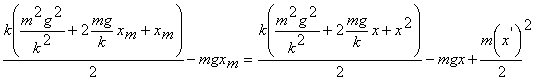
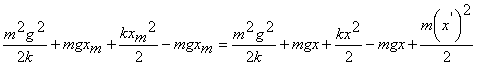
 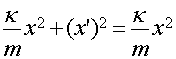 =соnst =соnst (6)
Как видно уравнения колебаний горизонтального и вертикального пружинных
маятников одинаковы.
Ускорение свободного падения g, имеющееся в уравнении (5), отсутствует в
полученном уравнении колебаний. Следовательно, колебания груза на пружине не
зависят от g и одинаковы, например, на Земле и Луне.
Хотя в дифференциальные уравнения (1) и (6) входят разные величины,
математически они эквивалентны.
По аналогии с уравнением (4) описывающем процессы в колебательном контуре,
запишем уравнение колебания пружинного маятника: (6)
Как видно уравнения колебаний горизонтального и вертикального пружинных
маятников одинаковы.
Ускорение свободного падения g, имеющееся в уравнении (5), отсутствует в
полученном уравнении колебаний. Следовательно, колебания груза на пружине не
зависят от g и одинаковы, например, на Земле и Луне.
Хотя в дифференциальные уравнения (1) и (6) входят разные величины,
математически они эквивалентны.
По аналогии с уравнением (4) описывающем процессы в колебательном контуре,
запишем уравнение колебания пружинного маятника:
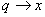 ; ; 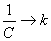 ; ; 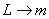 получим
получим
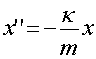 , (7)
Отклоним теперь математический маятник длиной l (рис. 3) от положения равновесия
на длину дуги sm<<l и отпустим.
Мгновенная высота подъема маятника
рис.3 , (7)
Отклоним теперь математический маятник длиной l (рис. 3) от положения равновесия
на длину дуги sm<<l и отпустим.
Мгновенная высота подъема маятника
рис.3

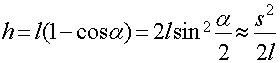 так как при a<<1 можно считать
так как при a<<1 можно считать 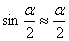 , а s=la. По закону сохранения энергии имеем: , а s=la. По закону сохранения энергии имеем:
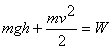 , где , где 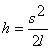
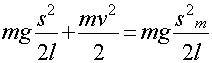 или
или
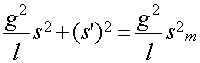 =const (8)
По аналогии с формулами (4) и (7) x®q®s; =const (8)
По аналогии с формулами (4) и (7) x®q®s; 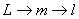 ; ; 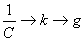 получаем:
S``= - получаем:
S``= - 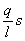 (9)
Различие уравнений (1), (6) и (9) состоит только в обозначениях и физическом
смысле входящих в них величин.
Если не предполагать sm<<l (соответственно am= (9)
Различие уравнений (1), (6) и (9) состоит только в обозначениях и физическом
смысле входящих в них величин.
Если не предполагать sm<<l (соответственно am=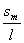 <<1 рад.), то получится сложное уравнение, решить которое в рамках
школьного курса невозможно. Оно будет описывать колебания, период которых
зависит от амплитуды. Строго говоря, период колебаний маятника всегда зависит
от am, однако при sm<<l рад. этой зависимостью
можно пренебречь.
Процессы в колебательном контуре станут понятнее учащимся при рассмотрении
преобразований энергий, которые происходят при колебаниях, используя таблицу
2.
<<1 рад.), то получится сложное уравнение, решить которое в рамках
школьного курса невозможно. Оно будет описывать колебания, период которых
зависит от амплитуды. Строго говоря, период колебаний маятника всегда зависит
от am, однако при sm<<l рад. этой зависимостью
можно пренебречь.
Процессы в колебательном контуре станут понятнее учащимся при рассмотрении
преобразований энергий, которые происходят при колебаниях, используя таблицу
2.
| Время | Колебательный контур | Пружинный маятник | 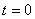
| На конденсаторе находится заряд q0; энергия электрического поля Wэ максимальна. Энергия магнитного поля Wм равна нулю 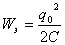 ; ; 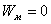
| Смешение X0 тела от положения равновесия — наибольшее; его потенциальная энергия Wп максимальна, кинетическая Wк равна нулю 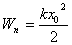 ; ;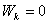
| 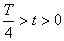
| При замыкании цепи конденсатор начинает разряжаться через катушку: возникает ток и связанное с ним магнитное поле. Вследствие самоиндукции сила тока нарастает постепенно; энергия электрического поля преобразуется в энергию магнитного поля 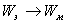
| Тело приходит в движение, его скорость возрастает постепенно. Потенциальная энергия преобразуется в кинетическую 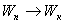
| 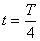
| Конденсатор разрядился, сила тока I0 максимальна, энергия электрического поля равна нулю, энергия магнитного поля максимальна Wэ=0; 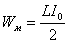 | При прохождении положения равновесия скорость v0, тела и его кинетическая энергия максимальны, потенциальная энергия равна нулю Wп=0; 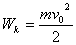 | 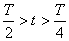
| Вследствие самоиндукции сила тока уменьшается постепенно; на конденсаторе начинает накапливаться заряд и 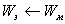
| Тело, достигнув положения равновесия, продолжает движение по инерции с постепенно уменьшающейся скоростью и 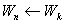
| 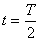
| Конденсатор перезарядился; сила тока в цепи равна нулю 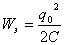 ; Wм=0 ; Wм=0
| Пружина максимально растянута: скорость тела равна нулю 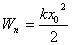 ; Wk=0 ; Wk=0
| 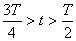
| Разрядка конденсатора возобновляется; ток течет в противоположном направлении; сила тока постепенно возрастает 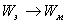
| Тело начинает движение в противоположном направлении с постепенно увеличивающейся скоростью 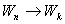
| 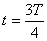
| Конденсатор полностью разрядился; сила тока I0 в цепи максимальна Wэ=0; 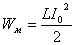 | Тело проходит положение равновесия, его скорость максимальна Wп=0; 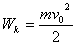 | 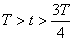
| Вследствие самоиндукции ток продолжает течь в том же направлении, конденсатор начинает заряжаться 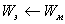 | По инерции тело движется к крайнему положению 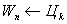
| 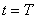
| Конденсатор снова заряжен, ток в цепи отсутствует, состояние контура аналогично первоначальному 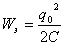 ; Wм=0 ; Wм=0
| Смещение тела максимально, его скорость равна нулю и состояние аналогично первоначальному 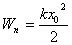 ; Wk=0 ; Wk=0
|
§ 2. Решение уравнений, описывающих колебания в пружинном и математическом
маятниках.
Найдем решение уравнения:
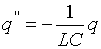 (1)
Нельзя считать, что (1)
Нельзя считать, что 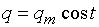 или или 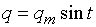 , так как вместо , так как вместо 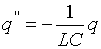 получилось бы равенство получилось бы равенство
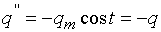 Чтобы в выражении второй производной
Чтобы в выражении второй производной 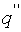 был множитель
был множитель 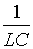 запишем уравнение (1) в виде:
запишем уравнение (1) в виде:
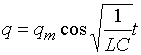 (2)
Найдем первую и вторую производные: (2)
Найдем первую и вторую производные:
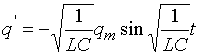
  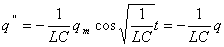 Функция (2) есть решение исходного уравнения (1). Функция
Функция (2) есть решение исходного уравнения (1). Функция
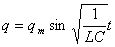 есть также решение исходного уравнения.
Обозначим постоянную величину есть также решение исходного уравнения.
Обозначим постоянную величину 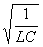 , зависящую от свойств системы, через
, зависящую от свойств системы, через  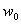 :
: 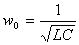 Тогда решение уравнения (2) можно записать:
Тогда решение уравнения (2) можно записать:
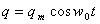 (3)
Тогда уравнение (1), описывающее свободные электромагнитные колебания примет
вид: (3)
Тогда уравнение (1), описывающее свободные электромагнитные колебания примет
вид:
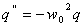 (4)
Из курса математики известно, что наименьший период косинуса равен 2π.
Следовательно, ω0=2π, (4)
Из курса математики известно, что наименьший период косинуса равен 2π.
Следовательно, ω0=2π,
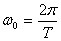 . Так как . Так как  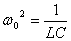 , тогда период колебаний равен , тогда период колебаний равен
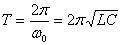 - формула Томсона.
Аналогично этим рассуждениям решим уравнение для колебаний вертикального
пружинного маятника: - формула Томсона.
Аналогично этим рассуждениям решим уравнение для колебаний вертикального
пружинного маятника:
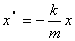 (5)
Запишем уравнение (5) в виде: (5)
Запишем уравнение (5) в виде:
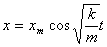 (6)
Найдем первую и вторую производные: (6)
Найдем первую и вторую производные:
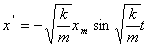
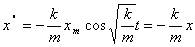 Функция (6) есть решение исходного уравнения. Функция
Функция (6) есть решение исходного уравнения. Функция 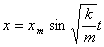 есть также решение исходного уравнения. Обозначим постоянную величину
есть также решение исходного уравнения. Обозначим постоянную величину
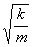 через w0 получим через w0 получим
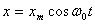 (7)
Тогда уравнение (5) будет иметь вид: (7)
Тогда уравнение (5) будет иметь вид:
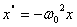 (8)
Период колебаний для пружинного маятника по аналогии с формулой Томсона (8)
Период колебаний для пружинного маятника по аналогии с формулой Томсона
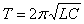 где
где 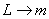 ; ; 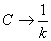 получим получим
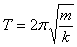 (9)
Аналогично выше изложенным рассуждениям решим уравнение для колебаний
математического маятника: (9)
Аналогично выше изложенным рассуждениям решим уравнение для колебаний
математического маятника:
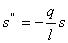 (10)
Запишем уравнение (10) в виде: (10)
Запишем уравнение (10) в виде:
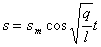 (11)
Найдем первую и вторую производные уравнения (11): (11)
Найдем первую и вторую производные уравнения (11):
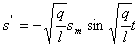
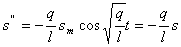 Функция (11) есть решение уравнения (10). Обозначим постоянную величину
Функция (11) есть решение уравнения (10). Обозначим постоянную величину 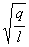 ,зависящую от свойств системы, через w0 получим:
,зависящую от свойств системы, через w0 получим:
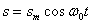 (12)
Тогда уравнение (10) примет вид: (12)
Тогда уравнение (10) примет вид:
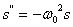 (13)
По аналогии с формулой(8) и формулой Томсона, для математического маятника
период колебаний равен: (13)
По аналогии с формулой(8) и формулой Томсона, для математического маятника
период колебаний равен:
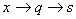 ; ; 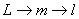 ; ; 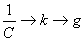
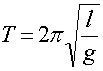 (14)
Уравнения (4), (8) и (13) являются решениями уравнений, описывающих колебания
в пружинном и математическом маятникам.
§ 3 Решение физических задач.
Рассмотрим несколько задач, решение которых методом аналогии возможно на
уроках и факультативных занятиях в 11 классах (после изучения раздела
"Электрические колебания) и при повторении материала.
Задача1. Изобразите механические системы, аналогичные электрическим цепям,
схематически изображенными на рис.1,а,б (14)
Уравнения (4), (8) и (13) являются решениями уравнений, описывающих колебания
в пружинном и математическом маятникам.
§ 3 Решение физических задач.
Рассмотрим несколько задач, решение которых методом аналогии возможно на
уроках и факультативных занятиях в 11 классах (после изучения раздела
"Электрические колебания) и при повторении материала.
Задача1. Изобразите механические системы, аналогичные электрическим цепям,
схематически изображенными на рис.1,а,б
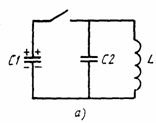 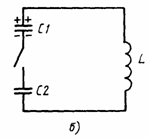 Решение. Аналогичная механическая система соответствующая рис.1,а,б
должна содержать тело массой m и две пружины с разными жестокостями
Решение. Аналогичная механическая система соответствующая рис.1,а,б
должна содержать тело массой m и две пружины с разными жестокостями 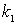 и
и 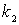 а) Общая емкость системы конденсаторов (рис.1,а) равна
а) Общая емкость системы конденсаторов (рис.1,а) равна
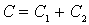 Используя аналогию механических и электрических величин, найдем что общая
жесткость пружин искомой механической системы находится из соотношения
Используя аналогию механических и электрических величин, найдем что общая
жесткость пружин искомой механической системы находится из соотношения
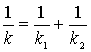 Это соответствует последовательному соединению двух пружин. Учитывая,
что один конденсатор заряжен, искомую механическую систему можно представить в
виде одной сжатой пружины жесткость
Это соответствует последовательному соединению двух пружин. Учитывая,
что один конденсатор заряжен, искомую механическую систему можно представить в
виде одной сжатой пружины жесткость 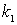 и одной недеформированной пружины жесткостью
и одной недеформированной пружины жесткостью 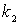 (рис.2,а).
б) Аналогично рассмотрим вторую схему.
Общая емкость системы конденсаторов (рис.1,б) равна
(рис.2,а).
б) Аналогично рассмотрим вторую схему.
Общая емкость системы конденсаторов (рис.1,б) равна
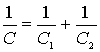 Используя аналогию механических и электрических величин, найдем что общая
жесткость пружин искомой механической системы находится из соотношения
Используя аналогию механических и электрических величин, найдем что общая
жесткость пружин искомой механической системы находится из соотношения
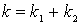 Это соответствует параллельному соединению двух пружин(рис.2,б).
Это соответствует параллельному соединению двух пружин(рис.2,б).
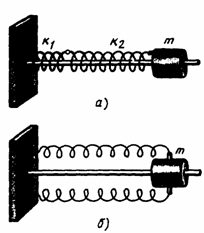 рис.2.
Задача2На рис.3,а,б изображены колебательные контуры. Придумайте
механические аналоги им. рис.2.
Задача2На рис.3,а,б изображены колебательные контуры. Придумайте
механические аналоги им.
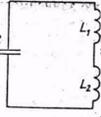 рис.3,а
О т в е т. Аналогичная механическая система соответствующая рис.3,а,б
должна содержать два тела массами
рис.3,а
О т в е т. Аналогичная механическая система соответствующая рис.3,а,б
должна содержать два тела массами 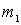 и
и 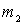 , и пружину
жесткостью k.
а) Общая индуктивность системы при последовательном соединении катушек равна , и пружину
жесткостью k.
а) Общая индуктивность системы при последовательном соединении катушек равна
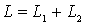 Используя аналогию механических и электрических величин найдем, что общая масса
Используя аналогию механических и электрических величин найдем, что общая масса
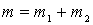 А это соответствует рис.4,а
А это соответствует рис.4,а
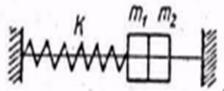 Рис. 4.а
б) Аналогично рассматриваем вторую схему.
Общая индуктивность параллельно соединенных катушек находится из соотношения
Рис. 4.а
б) Аналогично рассматриваем вторую схему.
Общая индуктивность параллельно соединенных катушек находится из соотношения
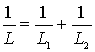 Используя аналогию механических и электрических величин, найдем что общая
масса катушек равна
Используя аналогию механических и электрических величин, найдем что общая
масса катушек равна
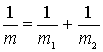 Это соответствует рис.4,б
Задача3. Придумайте механическую систему, которая была бы аналогична
электрической цепи, состоящей из конденсатора емкостью С и резистора
сопротивлением R (рис. 5). Первоначальный заряд конденсатора равен qм
. Ключ К замыкается в некоторый момент времени принимаемый за начальный.
Это соответствует рис.4,б
Задача3. Придумайте механическую систему, которая была бы аналогична
электрической цепи, состоящей из конденсатора емкостью С и резистора
сопротивлением R (рис. 5). Первоначальный заряд конденсатора равен qм
. Ключ К замыкается в некоторый момент времени принимаемый за начальный.
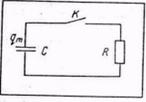 Рис. 5.
О т в е т. Электрическую цепь, состоящую из емкости и сопротивления,
можно представить как предельный случай электрического колебательного контура,
в котором индуктивность настолько мала, что ею можно пренебречь.
Поэтому аналогичная механическая система будет представлять собой прикрепленное
к пружине (жесткость К) тело с очень малой массой, но с значительным
объемом, находящееся в поле действия силы вязкого трения с коэффициентом
ß.
Задача4. Придумайте механическую динамическую аналогию электрической цепи,
представленной на рис. 6. В начальный момент катушка индуктивностью L и
резистор сопротивлением R отключены от источника постоянного тока с ЭДС
Рис. 5.
О т в е т. Электрическую цепь, состоящую из емкости и сопротивления,
можно представить как предельный случай электрического колебательного контура,
в котором индуктивность настолько мала, что ею можно пренебречь.
Поэтому аналогичная механическая система будет представлять собой прикрепленное
к пружине (жесткость К) тело с очень малой массой, но с значительным
объемом, находящееся в поле действия силы вязкого трения с коэффициентом
ß.
Задача4. Придумайте механическую динамическую аналогию электрической цепи,
представленной на рис. 6. В начальный момент катушка индуктивностью L и
резистор сопротивлением R отключены от источника постоянного тока с ЭДС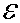 .
.
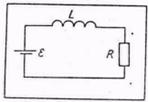 Рис. 6.
О т в е т. Аналогичная механическая система состоит из тела, находящегося
в поле тяжести Земли и расположенного внутри жидкости с коэффициентом вязкости
Р. Если отпустить это тело, то оно падает в жидкости под действием силы тяжести
FT= mg.
Задача5. Рассчитайте максимальное значение силы тока в цепи, изображенной на
рис.7. До замыкания ключа заряд на конденсаторе
Рис. 6.
О т в е т. Аналогичная механическая система состоит из тела, находящегося
в поле тяжести Земли и расположенного внутри жидкости с коэффициентом вязкости
Р. Если отпустить это тело, то оно падает в жидкости под действием силы тяжести
FT= mg.
Задача5. Рассчитайте максимальное значение силы тока в цепи, изображенной на
рис.7. До замыкания ключа заряд на конденсаторе  равен q, второй конденсатор не заряжен. Воспользуйтесь электромеханической
аналогией.
равен q, второй конденсатор не заряжен. Воспользуйтесь электромеханической
аналогией.
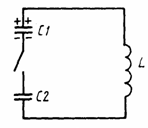 рис. 7.
Решение.
Здесь происходит превращение потенциальной энергии в кинетическую или в
соответствии с аналогией энергия электрического поля конденсатора
превращается в энергию магнитного поля катушки.
рис. 7.
Решение.
Здесь происходит превращение потенциальной энергии в кинетическую или в
соответствии с аналогией энергия электрического поля конденсатора
превращается в энергию магнитного поля катушки.
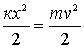 так как
так как 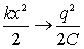 и и 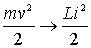 тогда
тогда
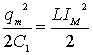 .
Отсюда значение максимальной силы тока равно .
Отсюда значение максимальной силы тока равно
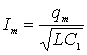 Задача 6. Найти максимальную скорость груза на пружине в вязкой среде при
действии на него переменной силы F=10sin10t(H) (рис. 8). Масса - груза 0,1 кг,
жесткость пружины 2 Н/м, вязкость среды 1 Н. м/с.
Задача 6. Найти максимальную скорость груза на пружине в вязкой среде при
действии на него переменной силы F=10sin10t(H) (рис. 8). Масса - груза 0,1 кг,
жесткость пружины 2 Н/м, вязкость среды 1 Н. м/с.
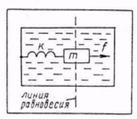 Рис.8
Р е ш е н и е. В связи с тем что такой более сложный процесс, какой
представлен в условии этой задачи, в школьном курсе физики не изучается, снова
обратимся к аналогии. Аналогичная электрическая система выглядит как
колебательный контур, содержащий внешний источник переменного тока (рис.
9).
Рис.8
Р е ш е н и е. В связи с тем что такой более сложный процесс, какой
представлен в условии этой задачи, в школьном курсе физики не изучается, снова
обратимся к аналогии. Аналогичная электрическая система выглядит как
колебательный контур, содержащий внешний источник переменного тока (рис.
9).
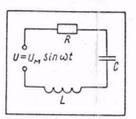 Рис.9
Из закона Ома для переменного тока (обозначения традиционные) максимальная
сила тока
Рис.9
Из закона Ома для переменного тока (обозначения традиционные) максимальная
сила тока
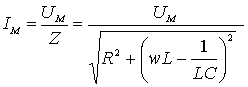 Установим соответствия характеристик механической и электрической систем: f
Установим соответствия характеристик механической и электрической систем: f U: ß
U: ß R
:m R
:m L:K L:K 1/C.
Учитывая аналогичность систем, получаем:
1/C.
Учитывая аналогичность систем, получаем:
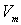 = =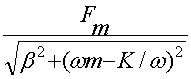 При подстановке следующих данных:
F=10Н,
При подстановке следующих данных:
F=10Н, 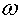 =10с-1, ß=1 Н•м/с, w=0,1кг, K=2 Н/м окончательно получаем vm =10с-1, ß=1 Н•м/с, w=0,1кг, K=2 Н/м окончательно получаем vm 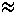 1,28 м/с.
Задача 7. Источник с ЭДС 1,28 м/с.
Задача 7. Источник с ЭДС 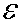 и нулевым внутренним сопротивлением соединен последовательно с катушкой
индуктивности L и конденсатором С (рис. 10). В начальный момент времени
конденсатор не заряжен. Найти зависимость от времени напряжения на конденсаторе
после замыкания ключа.
и нулевым внутренним сопротивлением соединен последовательно с катушкой
индуктивности L и конденсатором С (рис. 10). В начальный момент времени
конденсатор не заряжен. Найти зависимость от времени напряжения на конденсаторе
после замыкания ключа.
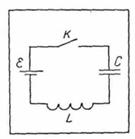 рис.10.
Решение. Искать нужную зависимость, используя законы электромагнетизма,
довольно сложно и не наглядно, поэтому целесообразно использовать механическую
аналогию. На рис.11 приведена аналогичная механическая колебательная система.
Аналогом источника с ЭДС может служить поле силы тяжести. При выдергивании
подставки из-под прикрепленного к пружине груза начинаются его колебания. Он
совершает гармоническое колебание около точки Xm, график
которого дан на рис. 12. а. Уравнение координаты имеет вид:
xm-x(t)=xm cos wot,
или
x(t)=xm (1 - cos wot).
рис.10.
Решение. Искать нужную зависимость, используя законы электромагнетизма,
довольно сложно и не наглядно, поэтому целесообразно использовать механическую
аналогию. На рис.11 приведена аналогичная механическая колебательная система.
Аналогом источника с ЭДС может служить поле силы тяжести. При выдергивании
подставки из-под прикрепленного к пружине груза начинаются его колебания. Он
совершает гармоническое колебание около точки Xm, график
которого дан на рис. 12. а. Уравнение координаты имеет вид:
xm-x(t)=xm cos wot,
или
x(t)=xm (1 - cos wot).
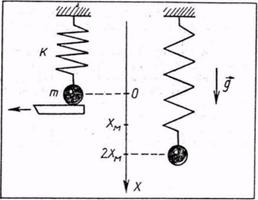 Рис. 11
Рис. 11
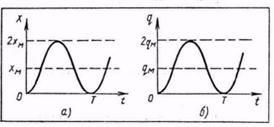 Рис. 12
Аналогичное электрическое колебание (график дан на рис. 12, б)
описывается следующими уравнениями:
q (t)=qм (1 – cos wot);
qм =
Рис. 12
Аналогичное электрическое колебание (график дан на рис. 12, б)
описывается следующими уравнениями:
q (t)=qм (1 – cos wot);
qм = 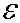 С, q (t)=C С, q (t)=C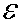 (1 — cos wot) ,
U(t)= (1 — cos wot) ,
U(t)= 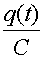 , U(f)= , U(f)= 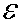 (1 — cos wot).
Здесь wo = (1 — cos wot).
Здесь wo =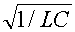 .
В заключение отметим, что рассмотренные нами аналогии широко используются в
научных исследованиях. Интересно, что принцип работы аналого-вычислительной
машины основан на «поразительной аналогичности» механического и
электрического процессов.
§4.Изучение волновых процессов.
Рассматривая вопроссы излучения и распространения любых волн, следует
сформулировать условия, необходимые для образования и излучения волн:
1) наличие источника колебаний в некоторой точке;
2) возможность передачи колебаний от данной точке к соседним (роль среды);
3) наличие достаточной связи источника колебаний с передающей средой.
Рассмотрим следующие волновые процессы: излучения и распространения
электромагнитных волн, интерференция света, дифракция света и поляризация
света.
1. Излучение и распространение электромагнитных волн.
При изучении вопросов излучения и распространения электромагнитных волн
целесообразным аналогом будут акустические волны, факт распространения
которых в окружающем пространстве легко устанавливается. Если взять
простейший источник акустических волн (камертон без резонансного ящика), то
связь его со средой малая и излучение звуковых волн незначительно. Поставив
камертон на резонирующий ящик, замечают, что излучение звука значительно
усилилось, так как связь со средой стала большей. Если рядом со звучащим
камертоном поставить другой камертон, имеющий ту же частоту, то такой
камертон возбуждается. Здесь наблюдают явление резонанса. Камертон, имеющий
другую частоту собственных колебаний, не возбудится. Излучение камертона
возможно только в среде, обладающей определенными физическими свойствами.
Как известно, излучение энергии замкнутым колебательным контуром
незначительно, так как электрическое поле в этом случае локализовано между
обкладками конденсатора, а магнитное поле — вокруг катушки. Чтобы подчеркнуть
это свойство замкнутого колебательного контура, уместно воспользоваться
аналогией с колеблющимся камертоном (без резонансного ящика), излучение
которого незначительно. Открытый колебательный контур излучает энергию
значительно лучше, так как в этом случае магнитное и электрическое поля
совмещены и занимают окружающее контур пространство. Чтобы проиллюстрировать
данный факт, уместна аналогия с камертоном на резонансном ящике, хорошо
излучающем энергию благодаря связи со средой.
Явление резонанса при звуковых процессах является хорошей аналогией для
объяснения приема электромагнитных волн. В антенне приемного устройства
возникают колебания всевозможных частот, но приемник «выбирает» из всех
колебаний только те, на частоту которых он настроен. Это аналогично
возбуждению камертона, имеющего ту же частоту, что и излучающий. При
излучении электромагнитных волн возникают возмущения в электромагнитном поле,
так же как возникают возмущения в упругой среде вокруг камертона. Природа же
распространяющихся при этом волн различна.
2.Интерференция света.
Интерференция света представляет собой сложное явление, объяснение которого
требует рассмотрения вопроса о наложении волн, об условиях усиления и
ослабления колебаний и т. д. Здесь применяют аналогию с поверхностными
волнами на воде.
Вначале, возбудив в волновой ванне две волны, наблюдают результат их
наложения и объясняют полученную картину(рис.1). .
В заключение отметим, что рассмотренные нами аналогии широко используются в
научных исследованиях. Интересно, что принцип работы аналого-вычислительной
машины основан на «поразительной аналогичности» механического и
электрического процессов.
§4.Изучение волновых процессов.
Рассматривая вопроссы излучения и распространения любых волн, следует
сформулировать условия, необходимые для образования и излучения волн:
1) наличие источника колебаний в некоторой точке;
2) возможность передачи колебаний от данной точке к соседним (роль среды);
3) наличие достаточной связи источника колебаний с передающей средой.
Рассмотрим следующие волновые процессы: излучения и распространения
электромагнитных волн, интерференция света, дифракция света и поляризация
света.
1. Излучение и распространение электромагнитных волн.
При изучении вопросов излучения и распространения электромагнитных волн
целесообразным аналогом будут акустические волны, факт распространения
которых в окружающем пространстве легко устанавливается. Если взять
простейший источник акустических волн (камертон без резонансного ящика), то
связь его со средой малая и излучение звуковых волн незначительно. Поставив
камертон на резонирующий ящик, замечают, что излучение звука значительно
усилилось, так как связь со средой стала большей. Если рядом со звучащим
камертоном поставить другой камертон, имеющий ту же частоту, то такой
камертон возбуждается. Здесь наблюдают явление резонанса. Камертон, имеющий
другую частоту собственных колебаний, не возбудится. Излучение камертона
возможно только в среде, обладающей определенными физическими свойствами.
Как известно, излучение энергии замкнутым колебательным контуром
незначительно, так как электрическое поле в этом случае локализовано между
обкладками конденсатора, а магнитное поле — вокруг катушки. Чтобы подчеркнуть
это свойство замкнутого колебательного контура, уместно воспользоваться
аналогией с колеблющимся камертоном (без резонансного ящика), излучение
которого незначительно. Открытый колебательный контур излучает энергию
значительно лучше, так как в этом случае магнитное и электрическое поля
совмещены и занимают окружающее контур пространство. Чтобы проиллюстрировать
данный факт, уместна аналогия с камертоном на резонансном ящике, хорошо
излучающем энергию благодаря связи со средой.
Явление резонанса при звуковых процессах является хорошей аналогией для
объяснения приема электромагнитных волн. В антенне приемного устройства
возникают колебания всевозможных частот, но приемник «выбирает» из всех
колебаний только те, на частоту которых он настроен. Это аналогично
возбуждению камертона, имеющего ту же частоту, что и излучающий. При
излучении электромагнитных волн возникают возмущения в электромагнитном поле,
так же как возникают возмущения в упругой среде вокруг камертона. Природа же
распространяющихся при этом волн различна.
2.Интерференция света.
Интерференция света представляет собой сложное явление, объяснение которого
требует рассмотрения вопроса о наложении волн, об условиях усиления и
ослабления колебаний и т. д. Здесь применяют аналогию с поверхностными
волнами на воде.
Вначале, возбудив в волновой ванне две волны, наблюдают результат их
наложения и объясняют полученную картину(рис.1).
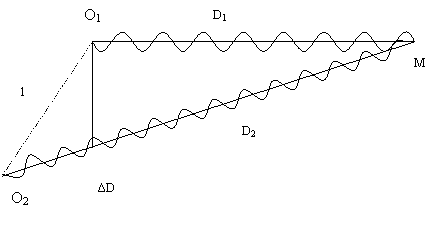 Рис.1.
В любой точке М на поверхности воды будут складываться колебания, вызванные
двумя волнами (от источников O1 и О2). Амплитуды
колебаний вызванных в т.М будут отличаться друг от друга, так как волны
проходят различные пути D1 и D2 .
Но если расстояние l между источниками много меньше этих путей (l <<D
1и l<<D2), то обе амплитуды можно считать одинаковыми.
Результат сложения волн в точке М зависит от разности фаз между ними. Пройдя
различные расстояния, волны имеют разность хода ΔD=D2-D1
Если разность хода равна длине волны l, то вторая волна запаздывает по
сравнению с первой ровно на один период. Следовательно, в этом случае гребни
(впадины) обеих волн совпадают.
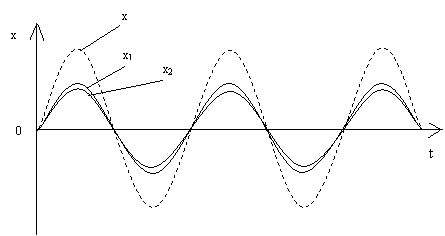
Сложение волн в зависимости от разности их хода объясняют на специально
вычерченных графиках, показывая, как складываются колебания при условии
совпадения фаз и в случае когда колебания происходят в противофазе.
Зависимость от времени смещения х1 и х2 вызванных двумя
волнами при DD=l. Разность фаз колебаний равна нулю, так как период синуса
равен 2p (рис.2).
Рис.1.
В любой точке М на поверхности воды будут складываться колебания, вызванные
двумя волнами (от источников O1 и О2). Амплитуды
колебаний вызванных в т.М будут отличаться друг от друга, так как волны
проходят различные пути D1 и D2 .
Но если расстояние l между источниками много меньше этих путей (l <<D
1и l<<D2), то обе амплитуды можно считать одинаковыми.
Результат сложения волн в точке М зависит от разности фаз между ними. Пройдя
различные расстояния, волны имеют разность хода ΔD=D2-D1
Если разность хода равна длине волны l, то вторая волна запаздывает по
сравнению с первой ровно на один период. Следовательно, в этом случае гребни
(впадины) обеих волн совпадают.
Сложение волн в зависимости от разности их хода объясняют на специально
вычерченных графиках, показывая, как складываются колебания при условии
совпадения фаз и в случае когда колебания происходят в противофазе.
Зависимость от времени смещения х1 и х2 вызванных двумя
волнами при DD=l. Разность фаз колебаний равна нулю, так как период синуса
равен 2p (рис.2).
Страницы: 1, 2
|

|

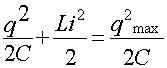 =const (2)
Следует заметить, что уравнение (2) так же следует из закона сохранения энергии.
В уравнении (2) i=q' - мгновенное значение силы тока, qmax
- максимальный заряд на конденсаторе (он не должен вызвать пробоя). Делаем
вывод о зависимости силы тока от величины заряда и находим значение
максимальной силы тока:
=const (2)
Следует заметить, что уравнение (2) так же следует из закона сохранения энергии.
В уравнении (2) i=q' - мгновенное значение силы тока, qmax
- максимальный заряд на конденсаторе (он не должен вызвать пробоя). Делаем
вывод о зависимости силы тока от величины заряда и находим значение
максимальной силы тока:
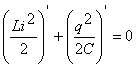 или
или
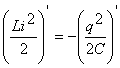 (3)
(3)
 Рис.2
Рис.2
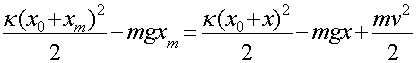 (5)
где X0=mg/k - статическое растяжение пружины (потенциальную
энергию груза в поле силы тяжести отсчитываем от уровня равновесия груза,
обозначенного на рис. 2 пунктиром). Учитывая, что
(5)
где X0=mg/k - статическое растяжение пружины (потенциальную
энергию груза в поле силы тяжести отсчитываем от уровня равновесия груза,
обозначенного на рис. 2 пунктиром). Учитывая, что 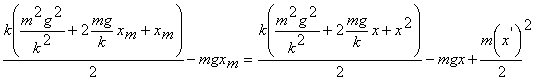
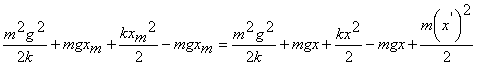
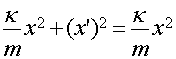 =соnst
=соnst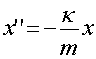 , (7)
Отклоним теперь математический маятник длиной l (рис. 3) от положения равновесия
на длину дуги sm<<l и отпустим.
Мгновенная высота подъема маятника
рис.3
, (7)
Отклоним теперь математический маятник длиной l (рис. 3) от положения равновесия
на длину дуги sm<<l и отпустим.
Мгновенная высота подъема маятника
рис.3

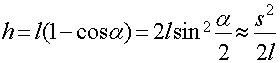 так как при a<<1 можно считать
так как при a<<1 можно считать 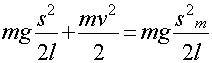 или
или
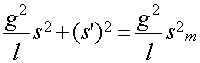 =const (8)
По аналогии с формулами (4) и (7) x®q®s;
=const (8)
По аналогии с формулами (4) и (7) x®q®s; 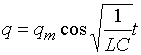 (2)
Найдем первую и вторую производные:
(2)
Найдем первую и вторую производные:
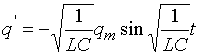
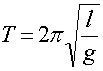 (14)
Уравнения (4), (8) и (13) являются решениями уравнений, описывающих колебания
в пружинном и математическом маятникам.
§ 3 Решение физических задач.
Рассмотрим несколько задач, решение которых методом аналогии возможно на
уроках и факультативных занятиях в 11 классах (после изучения раздела
"Электрические колебания) и при повторении материала.
Задача1. Изобразите механические системы, аналогичные электрическим цепям,
схематически изображенными на рис.1,а,б
(14)
Уравнения (4), (8) и (13) являются решениями уравнений, описывающих колебания
в пружинном и математическом маятникам.
§ 3 Решение физических задач.
Рассмотрим несколько задач, решение которых методом аналогии возможно на
уроках и факультативных занятиях в 11 классах (после изучения раздела
"Электрические колебания) и при повторении материала.
Задача1. Изобразите механические системы, аналогичные электрическим цепям,
схематически изображенными на рис.1,а,б

 Решение. Аналогичная механическая система соответствующая рис.1,а,б
должна содержать тело массой m и две пружины с разными жестокостями
Решение. Аналогичная механическая система соответствующая рис.1,а,б
должна содержать тело массой m и две пружины с разными жестокостями 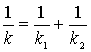 Это соответствует последовательному соединению двух пружин. Учитывая,
что один конденсатор заряжен, искомую механическую систему можно представить в
виде одной сжатой пружины жесткость
Это соответствует последовательному соединению двух пружин. Учитывая,
что один конденсатор заряжен, искомую механическую систему можно представить в
виде одной сжатой пружины жесткость 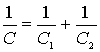 Используя аналогию механических и электрических величин, найдем что общая
жесткость пружин искомой механической системы находится из соотношения
Используя аналогию механических и электрических величин, найдем что общая
жесткость пружин искомой механической системы находится из соотношения
 рис.2.
Задача2На рис.3,а,б изображены колебательные контуры. Придумайте
механические аналоги им.
рис.2.
Задача2На рис.3,а,б изображены колебательные контуры. Придумайте
механические аналоги им.
 рис.3,а
О т в е т. Аналогичная механическая система соответствующая рис.3,а,б
должна содержать два тела массами
рис.3,а
О т в е т. Аналогичная механическая система соответствующая рис.3,а,б
должна содержать два тела массами  Рис. 4.а
б) Аналогично рассматриваем вторую схему.
Общая индуктивность параллельно соединенных катушек находится из соотношения
Рис. 4.а
б) Аналогично рассматриваем вторую схему.
Общая индуктивность параллельно соединенных катушек находится из соотношения
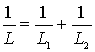 Используя аналогию механических и электрических величин, найдем что общая
масса катушек равна
Используя аналогию механических и электрических величин, найдем что общая
масса катушек равна
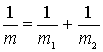 Это соответствует рис.4,б
Это соответствует рис.4,б
 Рис. 5.
О т в е т. Электрическую цепь, состоящую из емкости и сопротивления,
можно представить как предельный случай электрического колебательного контура,
в котором индуктивность настолько мала, что ею можно пренебречь.
Поэтому аналогичная механическая система будет представлять собой прикрепленное
к пружине (жесткость К) тело с очень малой массой, но с значительным
объемом, находящееся в поле действия силы вязкого трения с коэффициентом
ß.
Задача4. Придумайте механическую динамическую аналогию электрической цепи,
представленной на рис. 6. В начальный момент катушка индуктивностью L и
резистор сопротивлением R отключены от источника постоянного тока с ЭДС
Рис. 5.
О т в е т. Электрическую цепь, состоящую из емкости и сопротивления,
можно представить как предельный случай электрического колебательного контура,
в котором индуктивность настолько мала, что ею можно пренебречь.
Поэтому аналогичная механическая система будет представлять собой прикрепленное
к пружине (жесткость К) тело с очень малой массой, но с значительным
объемом, находящееся в поле действия силы вязкого трения с коэффициентом
ß.
Задача4. Придумайте механическую динамическую аналогию электрической цепи,
представленной на рис. 6. В начальный момент катушка индуктивностью L и
резистор сопротивлением R отключены от источника постоянного тока с ЭДС Рис. 6.
О т в е т. Аналогичная механическая система состоит из тела, находящегося
в поле тяжести Земли и расположенного внутри жидкости с коэффициентом вязкости
Р. Если отпустить это тело, то оно падает в жидкости под действием силы тяжести
FT= mg.
Рис. 6.
О т в е т. Аналогичная механическая система состоит из тела, находящегося
в поле тяжести Земли и расположенного внутри жидкости с коэффициентом вязкости
Р. Если отпустить это тело, то оно падает в жидкости под действием силы тяжести
FT= mg.
 рис. 7.
Решение.
Здесь происходит превращение потенциальной энергии в кинетическую или в
соответствии с аналогией энергия электрического поля конденсатора
превращается в энергию магнитного поля катушки.
рис. 7.
Решение.
Здесь происходит превращение потенциальной энергии в кинетическую или в
соответствии с аналогией энергия электрического поля конденсатора
превращается в энергию магнитного поля катушки.
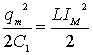 .
Отсюда значение максимальной силы тока равно
.
Отсюда значение максимальной силы тока равно
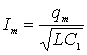 Задача 6. Найти максимальную скорость груза на пружине в вязкой среде при
действии на него переменной силы F=10sin10t(H) (рис. 8). Масса - груза 0,1 кг,
жесткость пружины 2 Н/м, вязкость среды 1 Н. м/с.
Задача 6. Найти максимальную скорость груза на пружине в вязкой среде при
действии на него переменной силы F=10sin10t(H) (рис. 8). Масса - груза 0,1 кг,
жесткость пружины 2 Н/м, вязкость среды 1 Н. м/с.
 Рис.8
Р е ш е н и е. В связи с тем что такой более сложный процесс, какой
представлен в условии этой задачи, в школьном курсе физики не изучается, снова
обратимся к аналогии. Аналогичная электрическая система выглядит как
колебательный контур, содержащий внешний источник переменного тока (рис.
9).
Рис.8
Р е ш е н и е. В связи с тем что такой более сложный процесс, какой
представлен в условии этой задачи, в школьном курсе физики не изучается, снова
обратимся к аналогии. Аналогичная электрическая система выглядит как
колебательный контур, содержащий внешний источник переменного тока (рис.
9).
 Рис.9
Из закона Ома для переменного тока (обозначения традиционные) максимальная
сила тока
Рис.9
Из закона Ома для переменного тока (обозначения традиционные) максимальная
сила тока
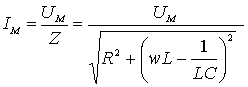 Установим соответствия характеристик механической и электрической систем: f
Установим соответствия характеристик механической и электрической систем: f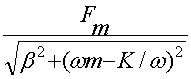 При подстановке следующих данных:
F=10Н,
При подстановке следующих данных:
F=10Н,  рис.10.
Решение. Искать нужную зависимость, используя законы электромагнетизма,
довольно сложно и не наглядно, поэтому целесообразно использовать механическую
аналогию. На рис.11 приведена аналогичная механическая колебательная система.
Аналогом источника с ЭДС может служить поле силы тяжести. При выдергивании
подставки из-под прикрепленного к пружине груза начинаются его колебания. Он
совершает гармоническое колебание около точки Xm, график
которого дан на рис. 12. а. Уравнение координаты имеет вид:
xm-x(t)=xm cos wot,
или
x(t)=xm (1 - cos wot).
рис.10.
Решение. Искать нужную зависимость, используя законы электромагнетизма,
довольно сложно и не наглядно, поэтому целесообразно использовать механическую
аналогию. На рис.11 приведена аналогичная механическая колебательная система.
Аналогом источника с ЭДС может служить поле силы тяжести. При выдергивании
подставки из-под прикрепленного к пружине груза начинаются его колебания. Он
совершает гармоническое колебание около точки Xm, график
которого дан на рис. 12. а. Уравнение координаты имеет вид:
xm-x(t)=xm cos wot,
или
x(t)=xm (1 - cos wot).
 Рис. 11
Рис. 11
 Рис. 12
Аналогичное электрическое колебание (график дан на рис. 12, б)
описывается следующими уравнениями:
q (t)=qм (1 – cos wot);
qм =
Рис. 12
Аналогичное электрическое колебание (график дан на рис. 12, б)
описывается следующими уравнениями:
q (t)=qм (1 – cos wot);
qм = Рис.1.
В любой точке М на поверхности воды будут складываться колебания, вызванные
двумя волнами (от источников O1 и О2). Амплитуды
колебаний вызванных в т.М будут отличаться друг от друга, так как волны
проходят различные пути D1 и D2 .
Но если расстояние l между источниками много меньше этих путей (l <<D
1и l<<D2), то обе амплитуды можно считать одинаковыми.
Результат сложения волн в точке М зависит от разности фаз между ними. Пройдя
различные расстояния, волны имеют разность хода ΔD=D2-D1
Если разность хода равна длине волны l, то вторая волна запаздывает по
сравнению с первой ровно на один период. Следовательно, в этом случае гребни
(впадины) обеих волн совпадают.
Сложение волн в зависимости от разности их хода объясняют на специально
вычерченных графиках, показывая, как складываются колебания при условии
совпадения фаз и в случае когда колебания происходят в противофазе.
Зависимость от времени смещения х1 и х2 вызванных двумя
волнами при DD=l. Разность фаз колебаний равна нулю, так как период синуса
равен 2p (рис.2).
Рис.1.
В любой точке М на поверхности воды будут складываться колебания, вызванные
двумя волнами (от источников O1 и О2). Амплитуды
колебаний вызванных в т.М будут отличаться друг от друга, так как волны
проходят различные пути D1 и D2 .
Но если расстояние l между источниками много меньше этих путей (l <<D
1и l<<D2), то обе амплитуды можно считать одинаковыми.
Результат сложения волн в точке М зависит от разности фаз между ними. Пройдя
различные расстояния, волны имеют разность хода ΔD=D2-D1
Если разность хода равна длине волны l, то вторая волна запаздывает по
сравнению с первой ровно на один период. Следовательно, в этом случае гребни
(впадины) обеих волн совпадают.
Сложение волн в зависимости от разности их хода объясняют на специально
вычерченных графиках, показывая, как складываются колебания при условии
совпадения фаз и в случае когда колебания происходят в противофазе.
Зависимость от времени смещения х1 и х2 вызванных двумя
волнами при DD=l. Разность фаз колебаний равна нулю, так как период синуса
равен 2p (рис.2).