Диплом: Контроль знаний и умений учащихся по математике в школе
включать в работу дополнительные задания для тех, кто работает быстрее.
2. Трудно подобрать задания одинаково посильные всем учащимся.
3. Трудно организовать проверку самостоятельных работ.
п.6.1.4. Организация контрольных работ
Контрольная работа может быть кратковременной и долговременной.
1. Перед проведением контрольной работы необходимо определить объект
контроля, цель предстоящей работы и средства контроля.
Они должны быть сообщены учащимся.
2. В зависимости от вида заданий нужно продумать, каким образом ученик
должен их оформить.
3. Учитель должен продумать что он отнесет к недочетам, а что к ошибкам.
Из этого будет складываться оценка. Критерии оценки хотя бы в общих чертах
должны быть известны учащимся.
4. Контрольная работа должна быть посильной для всех учащихся без
исключения. Сильным ученикам нужно дать задания труднее.
5. Каждой контрольной работе должна предшествовать самостоятельная
работа с аналогичными упражнениями.
6. Анализ контрольной работы необходимо проводить сразу, для этого
необходимо завершать работу за несколько минут до звонка. Желательно
фрагменты решения разобрать сразу после написания работы, потому что на
следующий день или позже учащиеся уже теряют интерес к содержанию работы и
многие интересуются только оценкой.
7. Обязательно нужно проводить количественный и качественный анализ
контрольной работы.
Данные количественного анализа удобно представлять в виде таблицы

Но данные количественного анализа не позволяют установить уровень владения
материалом конкретного ученика.
Такую возможность представляет качественный анализ. Информация, которая
подвергается качественному анализу, должна включать данные о выполнении
каждого задания предложенной контрольной работы каждым учеником класса.
Такие данные можно фиксировать в таблице.
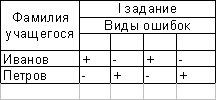
Содержание основной части таблицы свидетельствует об основных ошибках
учащихся, допущенных при выполнении отдельных заданий.
Анализ результатов контрольной работы может способствовать получению выводов
об особенностях своей деятельности по организации усвоения школьниками
учебного материала.
п.6.2. Машинные средства проверки
Для контроля знаний учащихся используют персональный компьютер. Д
ля контроля знаний учащихся удобно применять типовые расчеты, которые включают
наиболее характерные задания базового курса математики.
Перечислим некоторые преимущества использования компьютера для
создания типовых расчетов:
1.Однотипные задания печатаются в любом количестве неповторяющихся вариантов;
2.Варианты, созданные с помощью компьютерных программ,
проверяются значительно быстрее, так как компьютер может предоставить ответы к
каждому заданию;
3.Компьютерные типовые
задания удобны для отработки необходимых навыков с отстающими учащимися
(учитель не тратит время на подбор однотипных заданий для отработки
определенных навыков);
4.Учащиеся с огромным интересом работают с такими заданиями,
особенно, если карточка с заданием индивидуальна и ученик может работать в ней.
Глава II
Использование различных форм контроля на уроках математики.
Одним из существенных моментов в организации обучения является контроль за
знаниями и умениями учащихся. От того, как он организован, на что нацелен
существенно зависит содержание работы на уроке, как всего класса в целом, так
и отдельных учащихся. Вся система контроля знаний и умений учащихся должна
планироваться таким образом, чтобы охватывались все обязательные результаты
обучения для каждого ученика. Одновременно в ходе контроля надо дать учащимся
возможность проверить себя на более высоком уровне, проверить глубину
усвоения материала. В ходе изучения темы учитель проверяет результаты
обучения путем проведения текущих самостоятельных работ, устного опроса,
контрольных работ и других форм контроля
§1. Описание зачетной системы при изложении темы
“Тела вращения”.
Зачетная система включает в себя не только проведение зачетов, но и
предусматривает построение системы уроков.[12]
В этом параграфе рассмотрим, как используется эта система для контроля знаний
и умений учащихся по теме ”Тела вращения”. Эта система контроля была
опробована в школе №121 под руководством учителя Н.В. Алякринской.
Основная цель изучения темы – познакомить учащихся с простейшими телами
вращения и их свойствами.[20, c.165]
Рассмотрением простейших тел вращения завершается формирование системы
основных пространственных геометрических фигур, изучаемых в школьном курсе
стереометрии; в рассмотрение вводятся цилиндр, конус, шар и сфера.
Одновременно с определением конкретного тела вращения даются определения
большого числа понятий связанных с ним, усвоение которых должно идти не по
линии формального воспроизведения их определений, а в ходе решения
содержательных геометрических задач. В ходе их решения повторяются и
систематизируются сведения известные учащимся из курсов планиметрии и
стереометрии. При решении типичных задач этого раздела ученики должны
вычислять основные элементы данных тел (цилиндр, конус, шар), площади
сечений, используя свойства осевых сечений, свойства тел вращения.[18, c.
211]
При изложении темы “Тела вращения” учителем используется другое поурочное
планирование (не как в [19]):
1. лекция “Тела вращения” – 1 час
2. уроки – практикумы:
“цилиндр” – 2 часа
“конус” – 3 часа
“шар, сфера” - 3 часа
3. семинар по теме “Шар. Сфера” – 1 час
4. зачет по теме “Тела вращения” – 1 час
5. подготовка к контрольной работе – 1 час
6. контрольная работа – 1 час
п.1. лекция “Тела вращения”
цели урока – лекции:
1. Познакомить учащихся с понятиями: цилиндр, конус, шар, сфера, с их
основными элементами.
2. Выяснить знания учащихся по теме “Круг. Окружность”.
3. Развить пространственное воображение.
Ход урока:
I.Оргмомент.
II.Подготовка к изучению нового материала.
Перед тем, как изложить новый материал, необходимо проверить знания по теме
“Круг. Окружность”, которые нам потребуются при изучении темы “Тела
вращения”. В ходе фронтального опроса учащимся предлагается ответить на
следующие вопросы:
1. Назовите знакомые вам фигуры вращения (круг, окружность)
2. Чем отличается круг от окружности?
3. Дан отрезок АВ. Какая фигура получится при вращении вокруг точки А
точки В? (окружность)
5. Какую фигуру образует отрезок АВ при вращении его вокруг точки А? (круг с
центром в точке А и радиусом, равным отрезку АВ)
6. Какой многоугольник называется вписанным (описанным) в окружность?
III. Изложение нового материала.
Новый материал излагается в виде лекции по схеме:
1. определение тела вращения
2. основные элементы
3. сечения
4. вписанные и описанные многогранники
I. Цилиндр
1. 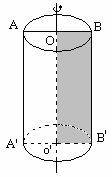 Цилиндр Цилиндр
– тело, которое состоит из двух кругов, не лежащих в одной плоскости и
совмещаемых параллельным переносом, и всех отрезков, соединяющих
соответствующие точки этих кругов.
Цилиндр получается при вращении прямоугольника вокруг стороны.
2. прямая OO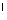 - ось цилиндра - ось цилиндра
отрезок OO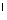 - высота, - высота,
отрезок АА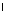 = ВВ = ВВ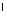 - образующая - образующая
круг (О,ОВ) =кругу (O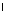 , O , O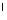 В В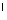 ) – основание цилиндра ) – основание цилиндра
3. а) осевое сечение (проходит через ось) есть прямоугольник
б) сечение цилиндра плоскостью, параллельной его оси, представляет собой
прямоугольник
в) сечение цилиндра плоскостью, перпендикулярной его оси, представляет собой
круг
4. а) призмой вписанной в цилиндр, называется такая призма, у
которой плоскостями оснований являются плоскости оснований цилиндра, а
боковыми ребрами – образующие.
б) Касательной плоскостью к цилиндру называется плоскость проходящая
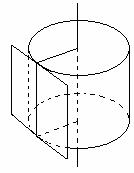 через образующую цилиндра и через образующую цилиндра и
перпендикулярная плоскости осевого сечения, содержащей эту образующую.
Призма описана около цилиндра, если у нее плоскостями оснований являются
плоскости оснований цилиндра, а боковые грани касаются цилиндра.
II. Конус
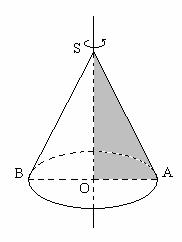
1. Конус – тело, которое состоит из круга – основания конуса,
точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков,
соединяющих вершину конуса с точками основания.
Конус получается при вращении прямоугольного треугольника вокруг катета.
2. т. S – вершина конуса
круг(О,ОА) – основание конуса
SA=SB – образующие конуса
Отрезок SO – высота конуса
Прямая SO – ось конуса
3. а) осевое сечение конуса – равнобедренный треугольник
б) сечение конуса плоскостью, проходящей через его вершину – равнобедренный
треугольник
в) сечение конуса плоскостью, перпендикулярно оси симметрии – круг
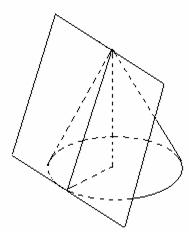 4. а) вписанная пирамида – 4. а) вписанная пирамида –
пирамида, основание которой есть многоугольник, вписанный в окружность
основания конуса, вершина – вершина конуса, боковые ребра пирамиды – образующие
конуса
б) Касательной плоскостью к конусу называется плоскость, проходящая через
образующую конуса и перпендикулярная плоскости осевого сечения, содержащей
эту образующую.
Описанная пирамида – пирамида, у которой основанием служит многоугольник,
описанный около основания конуса, вершина – вершина конуса, боковые грани –
касательные плоскости конуса.
II. 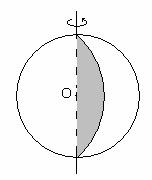 Шар. Сфера Шар. Сфера
1. Шар – тело состоящее из всех точек пространства,
находящихся на расстоянии не больше данного от данной точки.
Сфера – граница шара.
Шар получается при вращении полукруга вокруг его диаметра как оси
2. т. О – центр шара
ОА=ОВ – радиус шара
АВ – диаметр
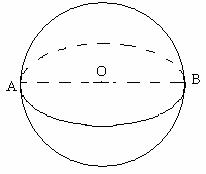
3. а) Всякое сечение шара плоскостью – круг, центром которого является
основание перпендикуляра, опущенного из центра шара на секущую плоскость.
б) плоскость, проходящая через центр шара – диаметральная плоскость. Сечение
шара диаметральной плоскостью называется большим кругом, а сечение сферы –
большой окружностью.
4.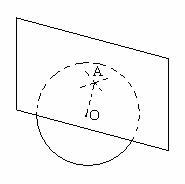 Плоскость проходящая через Плоскость проходящая через
точку А поверхности шара и перпендикулярная радиусу, проведенному в точку А,
называется касательной плоскостью, точка А – плоскостью касания.
а) многогранник называется вписанным в шар, если все его вершины лежат на
поверхности шара.
б) многогранник называется описанным около шара, если все его грани касаются
поверхности шара.
IV. Закрепление нового материала.
Для того, чтобы выяснить, как учащиеся усвоили новый материал, им
предлагается ответить на следующие вопросы, ответы на которые обсуждаются
всем классом:
1. Укажите среди окружающих вас предметов в природе, технике объекты,
имеющие формы цилиндра, конуса, шара
2. При вращении каких фигур получаются цилиндр, конус, шар, сфера?
3. При помощи моделей покажите и назовите основные элементы цилиндра, конуса,
шара
V. Сообщение домашнего задания.
VI. Подведение итогов урока.
п.2. Различные формы контроля на уроках – практикумах
В этом пункте остановимся, на различных формах контроля, которые применяются
на практических занятиях.
Известно, что чертеж является основным средством иллюстрации, развития
пространственного воображения.
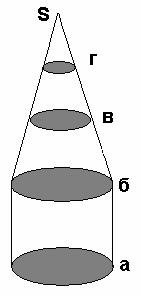
Для экономии времени на уроке и увеличении объема решаемых задач был
разработан шаблон для изображения тел вращения.[16] Этот шаблон предназначен
для изображения конуса и цилиндра, где заштрихованные части шаблона (а), (б),
(в), (г) вырезаются. Так например, если мы обведем основания (а) и (б) и
проведем касательные к ним, то получим изображение цилиндра. Если же обведем
одно из оснований (а) или (б), (в), (г) и заштрихуем точку S, из нее проведем
касательные к этим окружностям, то получим изображение конуса.
п.2.1. Тема “Цилиндр”
Приведем в этом пункте краткие конспекты уроков по теме “Цилиндр”.
Урок 1. Тема “Цилиндр”.
Цели урока:
1. Развить пространственное воображение.
2. Проверить знания по теме “Основные элементы цилиндра”.
3. Научить применять полученные знания к решению задач.
4. Закрепить знания по теме “Сечения цилиндра”.
Ход урока:
I. Оргмомент
II. Программированный опрос по теме “Основные элементы цилиндра”.
Цель программированного опроса – проверить как учащиеся усвоили тему. Это
задание высвечивается на экран с помощью кадоскопа. Учащиеся имеют два
листочка, на которых пишут ответы на вопросы. Один листок сдается учителю,
второй остается у ученика.
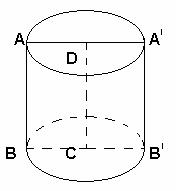 Приведем один из вариантов. Приведем один из вариантов.
На рисунке изображен цилиндр. Найдите:
I Радиус основания:
1. АВ 2.ВС 3.ВВ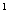 4.DA 4.DA
II Высоту
1. DC 2.DA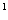 3.AA 3.AA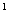 4.B 4.B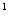 A A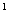
III образующую 1.BB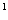 2.CD 3.BA 4.B 2.CD 3.BA 4.B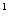 C C
IV осевое сечение 1.ADCB 2.ABB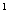 A A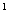 3.A 3.A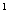 B B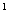 CD 4.BCDA CD 4.BCDA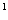
V основание 1.ABB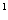 A A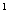 2.кр(B,BB 2.кр(B,BB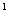 ) 3.кр(C,CB) 4. кр(C,BC) ) 3.кр(C,CB) 4. кр(C,BC)
После проведения такого опроса ученики сдают свои листки с ответами, а по
копиям сверяют ответы высвечиваемые с помощью кадоскопа. Все оценки за эту
работу выставляются в журнал.
III. Расширение и углубление знаний, умений и навыков учащихся.
Каждому ученику выдается подставка, штырь и проволока, из которой
предлагается выгнуть прямоугольник.
 Закрепив его на штыре, они Закрепив его на штыре, они
вращают его вокруг одной из его сторон. Вращая его, они получают наглядное
представление о цилиндре.
IV. Решение задач по теме “Сечение цилиндра, его основные элементы”.
На этом этапе ученики решают задачи на нахождение основных элементов
цилиндра, вычисляют площади сечений. В ходе решения задач требуется вспомнить
некоторые сведения из планиметрии и стереометрии. В связи с этим ученикам
предлагается ответить на следующие вопросы:
1. Какая фигура лежит в основании цилиндра?
2.Что такое осевое сечение цилиндра?
3. Что называется sin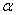 , cos , cos 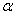 ? Чему равен sin 30 ? Чему равен sin 30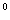 , sin 60 , sin 60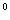 , cos 30 , cos 30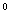 , cos 60 , cos 60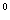
2. Какая фигура является сечением цилиндра плоскостью, параллельной оси?
3. Цилиндр катится по плоскости. Какая фигура получается при движении его
оси?
4. Чему равна площадь прямоугольника?
Кроме предложенных в учебнике Погорелова задач, на уроке используются задачи
взятые из других источников.[9]
V. Сообщение домашнего задания
VI. Подведение итогов урока
Урок 2. Тема “Цилиндр”.
Цели урока:
1. Закрепить основные понятия по темам “Сечения цилиндра”,
“Вписанные, описанные многогранники”.
2. Совершенствовать навыки решения задач по теме “Сечения
цилиндра”.
3. Проверить умения и навыки решения задач по теме “Сечения
цилиндра”.
4. Проверить практическое усвоение материала
Ход урока:
I Оргмомент
II Подготовка к изложению нового материала
Для того чтобы подготовить учащихся к решению задач по теме “Сечения
цилиндра”, а так же проведению самостоятельной работы по этой теме, в начале
урока проводится фронтальный опрос. Ученикам предлагается ответить на вопросы
альтернативного теста (ответы только “да” и “нет”).
I. Какие из следующих утверждений верны:
1. Любое сечение цилиндра плоскостью, перпендикулярной оси, есть окружность,
равная окружности основания.
2. Любое сечение цилиндра плоскостью, есть окружность, равная окружности
основания.
3. Плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному
основанию цилиндра.
II. Может ли осевое сечение цилиндра быть:
1. прямоугольником
2. квадратом
3. трапецией
III.
1. Какая плоскость называется касательной к цилиндру?
2. Какая призма называется вписанной в цилиндр?
3. Какая призма называется описанной около цилиндра?
III.Практическая работа.
Каждому ученику выдается подставка, штырь и проволока.
Задание: Выгнуть фигуру, при вращении которой получается цилиндр с
радиусом равным 10см и образующей равной 15 см.
IV. Решение задач по теме “Сечения цилиндра”, “Вписанная, описанная призма”.
V. Сообщение домашнего задания.
VI.Самостоятельная работа по теме “Сечения цилиндра”, “Основные элементы
цилиндра”.
Задачи, предлагаемые в самостоятельной работе, соответствуют обязательному
уровню математической подготовки.[18, c.211]
I Вариант
1. Осевое сечение цилиндра – квадрат, диагональ которого равна
20 см. Найдите высоту цилиндра.
2. Высота цилиндра равна 8 см, радиус равен 5 см. Найдите площадь сечения
цилиндра плоскостью параллельной его оси, если расстояние между этой
плоскостью и осью цилиндра равно 3 см.
II Вариант
1. Осевое сечение цилиндра – квадрат, диагональ которого равна
20 см. Найдите площадь основания цилиндра.
2. Высота цилиндра равна 12 см, радиус основания равен 10 см.
Цилиндр пересечен плоскостью, паралельной его оси так, что в сечении
получился квадрат. Найдите расстояние от оси цилиндра до секущей плоскости.
Все оценки за самостоятельную работу выставляются в журнал.
VI. Подведение итогов урока.
п.2.2. Тема “Конус”
По сравнению с темой “Цилиндр”, по теме “Конус” в учебнике Погорелова имеется
большее количество задач. На решение задач по теме “Конус” отводится 3 часа.
а) “Основные элементы, сечения конуса” – 1 час
б) “Сечения конуса. Усеченный конус” – 1 час
в) “Вписанные, описанные пирамиды” – 1 час
Урок 1. Тема “Конус”
Цели урока:
1.Развить пространственное воображение.
2. Закрепить основные понятия по темам “ Основные элементы, сечения конуса ”.
3. Проверить знаний по темам “ Основные элементы конуса ”, “ Сечения конуса ”.
4. Научить учеников применять полученные знания к решению задач.
Ход урока:
I Оргмомент
II Проверка домашнего задания
Домашнее задание было следующим: повторить пункты 1-3 лекции “Тела вращения”,
II часть “Конус” (основные элементы, определения, сечения). Перед тем как
решать задачи по теме “Конус”, в начале урока проводится самостоятельная
работа, все оценки за которую идут в журнал.
1. Завершить предложение:
конус это тело, которое состоит из .....
2. При вращении какой фигуры получается конус?
3. Сделать чертеж конуса, указать его основные элементы: вершину,
основание, образующие, высоту, ось конуса.
4. Как надо пересечь конус плоскостью, чтобы в сечении получить:
а) равнобедренный треугольник
б) круг
III. Расширение и углубление знаний, умений и навыков учащихся.
Каждому ученику выдается подставка, штырь и проволока, из которой
предлагается выгнуть треугольник.
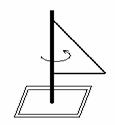 Закрепив его на штыре они Закрепив его на штыре они
вращают его вокруг его стороны. Вращая его так, они получают наглядное
представление о конусе.
IV. Решение задач по темам “ Основные элементы конуса ”, “ Сечения конуса ”.
В ходе решения задач ученикам задаются следующие вопросы:
1. Чему равна площадь круга? (Sкр = 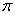 R R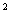 ) )
2. Чему равна площадь треугольника (S = 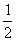 ab sin ab sin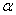 ) )
3. Что называется sin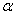 , cos , cos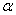 в прямоугольном треугольнике? в прямоугольном треугольнике?
4. Сформулируйте теорему Пифагора
V Сообщение домашнего задания.
V. Подведение итогов урока.
Урок 2. Тема “Сечения конуса. Усеченный конус”
Цели урока:
1. Развить пространственное воображение.
2. Совершенствовать навыки решения задач.
3. Проверить навыки решения задач по теме “Сечения, основные элементы конуса ”.
4. Проверить практическое усвоение материала.
Ход урока:
I Оргмомент
II Проверка домашнего задания
III Практическая работа.
Каждому ученику выдается подставка, штырь и проволока.
Задание: Выгнуть фигуру при вращении которой получается конус с радиусом
равным 5см и образующей равной 13 см.
IV Решение задач по теме “Сечения конуса”.
На этом уроке решаются задачи на сечение конуса, проходящего через вершину
конуса, а так же сечения конуса плоскостью перпендикулярной оси симметрии
конуса. В ходе решения задач ученикам задаются следущие вопросы:
1. Какой конус является усеченным?
2. Назовите основные элементы усеченного конуса.
3. Какой должна быть высота конуса, осевое сечение которого имеет ту же
площадь, что и его основание.
4. Основные отношения в прямоугольном треугольнике: sin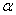 , cos , cos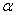 , tg , tg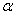 . .
5. Сформулируйте теорему Пифагора.
V Сообщение домашнего задания.
VI Самостоятельная работа по теме “Сечения конуса. Основные элементы конуса ”.
С целью улучшения качества решения задач используются тесты при проведении
самостоятельной работы.
Учащимся выдаются карточки, в которых предлагается решить задачи по готовому
чертежу, заполнив пропуски в первой задаче, и ответить на вопросы во второй
задаче.
Приведем пример этой работы:
Задача 1. Образующая конуса, равная 12 см, наклонена к плоскости
основания под углом 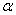
. Найдите площадь основания конуса, если 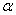
= 30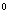 . .
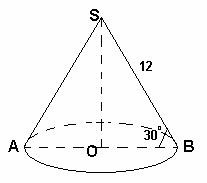 Дано: конус, SA=SB=12 см, Дано: конус, SA=SB=12 см, 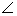 SBO=30 SBO=30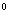
Найти: S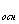
Решение:
1.  SOB – прямоугольный, в нем катеты – 1, гипотенуза – 2 SOB – прямоугольный, в нем катеты – 1, гипотенуза – 2
2. 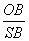 = cos30 = cos30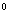 OB = 3, OB = 3,
ОВ = R (радиус основания)
3. В основании конуса лежит 4
4. S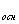 = =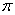 R R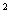 S S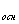 = 5 (см = 5 (см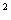 ) )
Ученики на листках записывают ответы с 1 по 5. После этого карточка ответов
выглядит следующим образом:
1. SO, OB
2. SB
3. SB cos30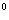 = =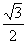 12 = 6 12 = 6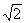
4. Круг
5. 72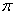
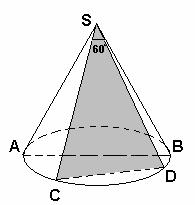 Задача 2. Осевое Задача 2. Осевое
сечение конуса – правильный треугольник, со стороной 2r . Найти площадь сечения
проведенного через две образующие конуса, угол между которыми равен 60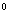
.
Дано:  SAB – правильный, SA=SB=AB=2r, SAB – правильный, SA=SB=AB=2r,
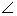 CSD = 60 CSD = 60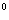
Найти: S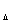 CSD CSD
Решение:
1. Какая фигура является сечением конуса плоскостью, проходящей через его
вершину?
2. Чему равны стороны SC и SD треугольника  CSD ? CSD ?
3. Выразить площадь треугольника через стороны треугольника и угол между
ними.
4. Чему равна площадь сечения (записать ответ).
VII Подведение итогов
Урок 3. Тема “Конус”
Страницы: 1, 2, 3
|



 Цилиндр
Цилиндр  через образующую цилиндра и
через образующую цилиндра и
 4. а) вписанная пирамида –
4. а) вписанная пирамида – Шар. Сфера
Шар. Сфера
 Плоскость проходящая через
Плоскость проходящая через
 Приведем один из вариантов.
Приведем один из вариантов. Закрепив его на штыре, они
Закрепив его на штыре, они Закрепив его на штыре они
Закрепив его на штыре они Дано: конус, SA=SB=12 см,
Дано: конус, SA=SB=12 см,  Задача 2. Осевое
Задача 2. Осевое