|
|
Диплом: Нестандартные задачи в курсе школьной математики (неполное и избыточное условие)
Диплом: Нестандартные задачи в курсе школьной математики (неполное и избыточное условие)
План
Вступление . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1. О роли задач в обучении математике . . . . . . . . . 2 2. Как учит решать задачи современная школа? . . . . 4 3. Формулировка проблемы . . . . . . . . . . . . . . . 10 I. Как ученики реагируют на «аномальные» задачи (констатирующие эксперименты) . . . . . . . . . . . . . . 17 II. Обоснование целесообразности задач с «аномальным» условием . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 III. Прикидка методического подхода к обучению решению «аномальных» задач . . . . . . . . . . . . . . . . . 32 IV. Расширенная система задач по теме «Сумма углов треугольника» . . . . . . . . . . . . . . . . . . . . . . . . . . 37 Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 Список литературы . . . . . . . . . . . . . . . . . . . . . . . . 52 | |
Вступление
1. О роли задач в обучении математике
В обучении математике задачам всегда отводилась достаточно большая, если не
решающая, роль.
Сейчас всё большее распространение получает прогрессивный метод обучения
через задачи как реализация системы проблемного обучения. Основные идеи этого
метода находят в какой–то мере отражение в новых учебниках. Задачи становятся
не только и не столько целью, сколько средством обучения.
Исторически сложилось, что на ранних этапах развития математики решение задач
было целью обучения. Ученик должен был заучить образцы и затем подводить под
эти образцы решения задач. В основном решались типовые, стандартные задачи,
принадлежащие классам алгоритмически разрешимых задач, т.е. таких, для
которых существует общий метод (алгоритм) решения.
Многообразные ситуации, возникающие на математическом и нематематическом
материале, приводят как к стандартным, так и нестандартным задачам, алгоритм
решения которых либо неизвестен, либо не существует.
В последние десятилетия постепенное изменение целей обучения математике
приводит к необходимости учить детей решению не только стандартных, но и
нестандартных задач, которые нельзя отнести к классу алгоритмически
разрешимых. Именно по отношению к нестандартной задаче возникает
необходимость в вариативном поиске решения.
"Задача предполагает необходимость сознательного поиска соответствующего
средства для достижения ясно видимой, но непосредственно не доступной цели.
Решение задач означает нахождение этого средства". [17, с. 143]
Определённые группы задач, предназначенных для классных и внеклассных
занятий, вполне пригодны для выработки "надлежащих навыков мысли", навыков,
направленных на поиски решения задач.[6, с. 119-120]
В книге [13, с. 165] М. И. Махмутов рассказывает об исследовании, проведённом
группой учёных, математиков и психологов с целью выявления закономерностей
активизации познавательной деятельности учащихся. Вот что он пишет в книге:
"Теоретическое осмысление работ лучших учителей помогло обнаружить в учебном
процессе общую закономерность активизации познавательной деятельности
учащихся: напряжение интеллектуальных сил ученика вызывается главным образом
постановкой проблемных вопросов, проблемных познавательных задач и учебных
заданий исследовательского характера. Это напряжение рождается в столкновении
с трудностью в понимании и осмыслении нового факта или понятия и
характеризуется наличием проблемной ситуации, высокого интереса учащегося к
теме, его эмоционального настроя и волевого усилия."
Роль задач в обучении математике невозможно переоценить. Через задачу
естественно ввести проблемную ситуацию. Разрешив систему специально
подобранных задач, ученик знакомится с существенными элементами новых
алгоритмов, овладевает новыми техническими элементами. Применять
математические знания в жизненных ситуациях учат соответствующие практические
задачи. [11, с.182]
Итак, как видно из приведённого выше обзора мнений различных специалистов в
области образования и обучения математике, задача является основным звеном
внутри процесса обучения, а тем более такого, как проблемное и развивающее.
2. Как учит решать задачи современная школа?
Однако использование задач в процессе обучения математике и в настоящее время
ещё далеко от совершенства.
Как пишет А.Эсаулов [25, с.8] в психологии и педагогике обращается внимание
преимущественно на то, как решаются уже кем–то найденные и вполне чётко
сформулированные задачи, а не на то, как они обнаруживаются и ставятся. В
результате получается, что человек, привыкший видеть перед собой чётко и
корректно сформулированную задачу, просто теряется в незнакомой ситуации,
будь то хоть обычная некорректная математическая задача или некая задача,
возникшая как следствие из практики (прикладная).
В современном математическом образовании (мы ориентируемся на страны бывшего
СССР) отмечается следующий актуальный аспект: изучение математики на всех
этапах должно иметь развивающий характер и прикладную направленность.
Молодёжи необходимо давать не просто конкретную сумму знаний, но и прививать
ей навыки творчества, интерес к исследованию, формировать у неё положительную
мотивацию. [11, с.136]
Интерес к учебной деятельности, подкрепляемый постоянным активным участием в
открытии новых истин, проверке гипотез, поиском способа действий в задаче,
является основным психологическим условием успешности этой деятельности. [11,
с.129]
Школьные уроки математики по–прежнему нацелены на прохождение программы, а не
на развитие мышления у детей. Учитель видит свою задачу в том, чтобы
школьники с его помощью усвоили ещё одну порцию материала. Однако главная его
задача – всемерно содействовать развитию познавательных возможностей у
учащихся.[11, с.178]
Основную часть времени на уроке ученик проводит, решая задачи, и во многом от
их особенностей (сложности, многогранности, сюжетной формы,
последовательности и др.) и зависит, насколько успешным будет процесс
обучения математике. Но что же мы имеем на самом деле? На практике
получается, что чаще всего процесс решения задач на уроке обладает некоторой
рутинностью и оставляет ученику мало возможностей для творчества. Со временем
такая специфика задач вырабатывает у ученика некоторый неправильный стереотип
мышления, относящийся к решению задач. Ученик просто ищет стандартную
ситуацию, к которой можно было бы применить известные формулы и теоремы, и
теряется, когда предложенная задача требует даже несложного нестандартного
подхода.
По мнению Л.Фридмана, одной из основных в обучении математике функций задач
является функция формирования и развития у учащихся общих умений решений
любых математических (в том числе и прикладных) задач.
Учащиеся же в настоящее время не получают никаких специальных знаний, на базе
которых возможно такое формирование. Более того, в настоящее время эти общие
умения формируются чисто стихийно, а не в результате целенаправленного,
систематического обучения. Считается, что эти умения могут возникнуть лишь
благодаря решению большого числа математических задач. [22, с.151-152]
Анализ школьных учебников математики показывает, что они содержат вроде бы
достаточное (или даже избыточное) количество задач, из которых учитель может
составлять наборы задач, ориентированные на разные классы и на разных
учащихся. Однако учебный эффект получается, по мнению многих
педагогов–исследователей, с которым мы вполне согласны, невысоким.
Большинство учащихся, встретившись с задачей незнакомого или малознакомого
вида, не знают, как к ней подступиться, с чего начать решение, и при этом
обычно произносят печально известные слова: "А мы такие не решали".
Каковы же причины этого широко распространённого явления?
Автор книги [14] видит основную причину в неудовлетворительной постановке
задач в обучении математике. Он пишет: "Проблема постановки задач в процессе
обучения математике до сих пор не нашла удовлетворительного решения (ни в
нашей стране, ни за рубежом) ни с точки зрения содержания учебных задач, ни с
точки зрения их целевого назначения, ни с точки зрения числа обязательных или
необязательных задач или представления их в виде целостной системы."
Сейчас, когда учащиеся не имеют систематических знаний о задачах и сущности
их решения, главное внимание учащихся (и учителей) направлено на то, чтобы
найти решение задачи и притом как можно быстрей. На заключительный анализ, на
установление того, какие выводы можно сделать из выполненного решения, – на
всё это уже не остаётся ни сил, ни времени, ни желания, а ведь это едва ли не
главные аспекты решения задач.
В школе невозможно, да и не нужно, рассматривать все виды математических
задач. Сколько бы задач ни решали в школе, всё равно учащиеся в своей будущей
работе встретятся с новыми видами задач. Поэтому школа должна вооружать
учащихся общим подходом к решению любых задач.
Одной из особенностей математики является алгоритмичность решения многих её
задач. Алгоритмом, как известно, называется определённое указание относительно
того, какие операции и в какой последовательности надо выполнить, чтобы решить
любую задачу определённого типа. Конечно, очень большое количество задач не
алгоритмизируется и решается с помощью специальных, особых приёмов. Поэтому
способность находить пути решения, не подходящие под стандартное
правило, является одной из существенных особенностей математического мышления,
как об этом пишет в своей книге академик Колмогоров. [7, с.76]
Необходимость специальных способностей для изучения и понимания математики
часто преувеличивают. Впечатление исключительной трудности математики иногда
создаётся её плохим, чрезмерно формальным изложением на уроке.
Умение последовательно, логически рассуждать в незнакомой обстановке
приобретается с трудом. На математических олимпиадах самые неожиданные
трудности возникают именно при решении задач, в которых не предполагается
никаких предварительных знаний из школьного курса, но требуется правильно
уловить смысл вопроса и рассуждать последовательно. [7, с.80]
Многие нарекания вызывает и подготовка школьников как абитуриентов,
поступающих в ВУЗы на физико–математические специальности. Многолетняя
практика приёмных экзаменов показывает, что воспитанные в традиционной школе
абитуриенты обладают знаниями, достаточными для поступления в ВУЗ, однако
интеллектуальное развитие большинства из них и, прежде всего, уровень
абстрактного и логического мышления недостаточен для эффективного обучения по
выбранной специальности.[11, с. 92]
Итак, как показывает вышеизложенный анализ литературы, наборы задач имеющихся
школьных учебников пока ещё не удовлетворяют требованиям, предъявляемым к
результативности математического образования. Чаще всего, эти задачи
относятся к алгоритмически разрешимым, не развивают у учеников вариативного
мышления, не учат множеству навыков, столь необходимых для решения задач, как
школьных, так и бытовых, производственных, научных и т. д.
Рассмотрим более детально, как обстоит дело с задачами, представленными в
действующих учебниках математики.
Анализ школьных учебников математики показывает, что с 5–го по 11–й класс
ученики решают более 7000 задач. [11, с.171]
Если взглянуть на задачи, представленные в школьных учебниках математики, то
все задачи, содержащиеся в них, внутри одной темы классифицированы по степени
сложности и расположены, как правило, в порядке её возрастания.
Среди предлагаемых учащимся задач представлены задачи разных классификаций
(по крайней мере, к этому стремятся авторы учебников): по их назначению –
тренировочные и развивающие, по наличию алгоритма решения – стандартные и
нестандартные, по характеру требования – доказательные, вычислительные и
конструктивные. Есть и другие классификации, находящие то или иное отражение
в школьных учебниках.
3. Формулировка проблемы
Но одна из классификаций почти не находит отражения в действующих учебниках
за редкими исключениями. Речь идёт о классификации по характеру условия
задачи – определённые, неопределённые и переопределённые. Школьникам
преимущественно предлагаются задачи определённые, т.е. задачи, содержащие в
условии ровно столько данных, сколько их требуется для получения ответа, не
больше и не меньше. Но почему не больше и не меньше?
Если учитель ставит целью научить своих учеников решать задачи из жизни, а не
из учебников, то он должен научить их: 1) математизировать ситуацию (т.е.
переводить задачу бытовую, производственную и др. на язык математики); 2)
выбирать необходимые для решения величины из их чрезмерного множества или
осуществлять вариативный поиск данных, недостающих для решения задачи; 3)
решать полученную математическую задачу; 4) анализировать найденные решения,
сравнивать их, выбирать наиболее экономичные; 5) разматематизировать ситуацию
(т.е. переводить полученный ответ на язык бытовой, производственной и прочей
практики).
Из перечисленных видов деятельности школа учит разве что третьему. Остальные
затрагиваются в такой ничтожной мере, что говорить даже о частичном обучении
здесь вряд ли следует. Например, если вспомнить о задачах неопределённых и
переопределённых, то таких в современных учебниках насчитывается не более
полупроцента, да и тех учителя чаще всего не замечают.
Приятным исключением из указанного правила является учебник [18]. Его автор,
профессор Н.Рогановский, предлагает задачи под рубриками, среди которых есть
и такие: «Все ли возможные случаи рассмотрены?», «Достаточно ли данных для
решения задачи?», «Сколько решений имеет задача?» и т. п. Естественно,
задачи, предлагаемые под этими рубриками, соответствуют поставленному
вопросу, т.е. имеют несколько вариантов реализации условия, несколько
возможных путей решения, и количество данных в условии не обязательно
является необходимым и достаточным для получения ответа.
Но, как уже сказано, этот учебник – исключение. Большинство авторов других
учебников такие задачи игнорируют. Может быть, считают их бесполезными и
ненужными в обучении?
Однако, многие известные педагоги–исследователи считают использование таких
задач полезным и необходимым.
Например, М.Крутецкий в своей книге "Психология математических способностей
школьников" приводит такую классификацию:
1. Задачи с несформированным условием – задачи, в которых имеются все данные,
но вопрос задачи лишь подразумевается.
2. Задачи с избыточным условием – задачи, в которых имеются лишние данные, не
нужные для решения, а лишь маскирующие необходимые для решения задачи данные.
3. Задачи с неполным составом условия – задачи, в которых отсутствуют
некоторые данные, необходимые для решения задачи, вследствие чего дать
конкретный ответ на вопрос задачи не всегда представляется возможным.
4. Задачи с противоречивым условием – задачи, содержащие в условии
противоречие между данными. [9, с. 124-150]
В.А.Крутецкий описывает исследование, которое он с группой исследователей
проводил во многих школах СССР в течение 12 лет с 1955 по 1966 годы.
Исследователи использовали задачи различных типов, среди которых были и
приведённые в этой классификации, в качестве тестовых заданий для выявления
психологических аспектов математических способностей школьников. По
результатам этого исследования получилось, что сильные ученики справляются с
задачами указанных типов практически самостоятельно, быстро, практически без
помощи испытателя. Ученики средних способностей также неплохо справляются с
подобными заданиями, однако для их решения им требуется больше времени и
иногда наводящий вопрос, наталкивающий на решение. Слабые ученики практически
не могли самостоятельно провести решение этих задач, не видели связи между
объектами задачи, и даже с подсказкой испытателя не могли справиться с
заданием.
Следует отметить, что именно с указанными типами задач исследователи
связывали наибольшие надежды.
В книге Д.Пойа "Как решать задачу" приводится похожая классификация,
отличающаяся лишь тем, что в ней отсутствуют задачи с несформированным
составом условия. Более того, в своей таблице, направленной в помощь
решателю, Д.Пойа первыми пунктами поставил вопросы: Возможно ли удовлетворить
условию? Достаточно ли условие для определения неизвестного? или
недостаточно? или чрезмерно? или противоречиво?
Вроде бы Пойа предполагает решение самых обычных, школьных задач, однако он
не исключает возможности наличия некоторых "аномалий" в условии задачи, к
существованию которых ученики должны быть готовы.
П.Эрдниев в своей книге [24, ñ.24,40] предлагает использовать в обучении
математике задачи с неполным составом условия ещё с младших классов, причём он
считает, что использование таких задач (деформированных примеров, как он их
называет) позволяет проводить обучение опережающими темпами, с их помощью можно
коренным образом изменить мыслительные процессы решающего, превратив их в более
сложные, более содержательные и потому лучше развивающие способности ученика.
У Н.Метельского встречается такая классификация задач. Между условием задачи (А)
и её требованием (Х) может быть различное соотношение, определяющее число
решений. Обычно школьная задача имеет одно или несколько определённых решений и
потому называется определённой. Этот тип задачи условно можно изобразить
формулой импликации А=>Х, которую будем понимать так, что условие А содержит
достаточно и только достаточно данных для выполнения требования Х. Если из
условия А какое–либо данное опустить, то получим неопределённую задачу. Она
имеет бесконечное множество решений, зависящих от бесконечного множества
значений той величины (параметра), которой принадлежало значение, выброшенное
из условия. Наконец, условие может содержать, кроме А, некоторое дополнительное
данное, и тогда задача называется переопределённой. В частном случае это
"лишнее" данное может вытекать из тех, что уже имеются в задаче, и тогда задача
оказывается определённой задачей. В остальных случаях переопределённая задача
не имеет решения, поскольку её данные противоречат друг другу, несовместимы.
Основные функции задач в обучении выполняют определённые задачи, однако
известную пользу, по мнению Н.Метельского, приносит учащимся знакомство с
неопределёнными и переопределёнными задачами. [14, с.176-177]
Задачи из рассматриваемой классификации полезны тем, что: они не обладают
алгоритмичностью решения, они активизируют умственную деятельность учащихся,
заставляют их искать нестандартные подходы к решению задач, а также допускают
как несколько способов решения, так и несколько решений вообще.
В подтверждение этого мнения интересные факты приводит в своей статье
"Остроугольный или тупоугольный?" И.Дегтянникова. Она пишет: "Решая задачу,
часто даже не задумываемся о реальности её условия. Поэтому правы те авторы,
которые включают в свои учебники задачи с нереальными условиями. Это
заставляет проверять условия у всех задач. Кроме того, нереальные задачи –
это готовая проблемная ситуация». [4]
Отсутствие указанных задач в школьных учебниках приводит к тому, что и
учителя не ориентируют свои умения на такие задачи, в результате чего их
педагогическая подготовка содержит изъяны.
В заметке [5] В.Игнатенко пишет об ошибке, найденной в учебнике [1]. В этом
учебнике на с.135 приведена задача 536(б). Вот её текст: "Отрезок BD является
биссектрисой треугольника АBC. Найдите DC, если AB=30, AD=20, BD=16 и
ÐBDC=ÐC.
Вроде бы ничего особенного в этой задаче нет. Однако автор, проведя решение
двумя различными способами, заметил, что ответы в них не совпадают. Попытка
смоделировать треугольник с данными, указанными в задаче, показала, что
данные содержали противоречие. Оказывается, маститые авторы популярного
учебника, включив противоречивую задачу в свой учебник, не заметили её
противоречивости, как не замечали её и тысячи учителей, несколько лет
работавших по этому учебнику.
Присутствие такой задачи (пока что только одной) в учебнике геометрии –
только на пользу ученикам и учителям. Жаль, что эта задача – результат
случайной оплошности авторского коллектива, а не результат её закономерного
выбора.
Как пишет М.Буловацкий в своей статье [2], школьник, как правило, игнорирует
важные вопросы о переизбыточности, недостаточности или противоречивости
задач, так как задачи из школьных учебников не требуют размышления над такими
вопросами, потому что в них практически всегда имеется столько данных,
сколько необходимо для решения. И это является, по мнению М.Буловацкого,
серьёзным недостатком математического образования школьников.
По результатам эксперимента, описанного в статье, переопределённые (с
избыточным составом условия) или неопределённые (с недостатком данных) задачи
ставят большинство школьников в тупик, из которого они зачастую не в
состоянии выбраться. И это затруднение возникает в связи с тем, что у
школьников не отработан навык отбора и предварительной оценки данных задачи.
Как считает М.Буловацкий, отработке этого навыка нужно уделять специальное
учебное время. [2]
Итак, анализ литературных источников выявляет важную для математического
образования проблему: многие педагоги–исследователи указывают на
целесообразность использования в обучении задач с «аномальными» условиями, а
авторы учебников на это указание почти не реагируют.
Нас заинтересовала эта проблема с разных точек зрения. Во–первых, насколько
полезно включение таких задач в школьный курс математики? Во–вторых, нужно ли
специальное обучение учащихся решению таких задач? И если нужно, то каковы
методические особенности такого обучения?
Поискам ответов на эти вопросы и посвящена настоящая работа.
I. Как ученики реагируют на «аномальные» задачи?
(констатирующие эксперименты)
Предварительно мы показали, что многие известные в педагогике учёные считают
полезным включение неопределённых и переопределённых задач в процесс
обучения. Почему же большинство учебников уделяет такое слабое внимание этим
задачам? Может быть, учащиеся и без специального обучения в состоянии решать
такие задачи? По крайней мере, выводы В.Крутецкого близки к утвердительному
ответу. Но имеются и другие мнения.
Чтобы ответить на этот вопрос, был проведён ряд констатирующих экспериментов
в разных классах.
Так, в период педагогической практики в 1997 году был проведен небольшой
эксперимент в средней школе № 3 г. Орша.
Ученикам 6 класса, в составе которого на момент проведения эксперимента было 25
человек, на самостоятельной работе в качестве дополнительного задания была
предложена следующая задача: в прямоугольнике стороны равны 8,4 см и 3,9
см, а периметр 24,6 см. Найти площадь прямоугольника. При решении этой
задачи в классе выделилось несколько групп: 1 ученик не решил её вообще,
мотивировав это тем, что не успел этого сделать; 2 ученика решили эту задачу
полностью с объяснением того, почему они не использовали при решении задачи
данный в ней периметр, но не проверили, соответствует ли данная длина периметра
длинам сторон; 1 ученик (кстати, участник областной олимпиады по математике)
решил эту задачу полностью и проверил соответствие в ней данных друг другу, но
при этом возился с решением около 10 минут, а остальные ученики просто написали
ответ к задаче без каких бы то ни было объяснений к нему.
После решения задания с учеником, полностью решившим задачу, была проведена
беседа о том, с какими трудностями он столкнулся в процессе решения задачи, и
выяснилось, что, решая эту задачу, он вначале думал, что в задаче даны два
прямоугольника, площадь одного из которых он нашел сразу же и долго вычислял,
как можно выразить площадь прямоугольника через его периметр. Но потом
проверил, что длина периметра полностью соответствует длинам сторон, и решил,
что в задаче речь идет об одном и том же прямоугольнике, а периметр дан только
для того, чтобы запутать решение. На следующем уроке класс изъявил желание
узнать, как же правильно решается эта задача. Им было подробно объяснено, что
периметр в задаче является лишним данным и его не нужно использовать для
решения, но в данной ситуации длины сторон в задаче соответствуют периметру,
что бывает не всегда и требует проверки. После чего была предложена для решения
задача аналогичного характера, но содержащая противоречие в тексте: в
прямоугольнике длины сторон равны 6,7 см и 4,2 см, а площадь равна 25,3 кв. см.
Требуется найти периметр прямоугольника. Как и ожидалось, все 25
учащихся решили эту задачу без использования площади и записали ответ. Все
посчитали, что площадь в задаче является лишним данным, но никто не счёл нужным
проверить, соответствуют ли данные друг другу. Результат самостоятельной работы
(отсутствие "пятёрок" в работе с несложными задачами) заставил их всё же
задуматься. Очередная беседа на ту же тему была воспринята ими уже с большим
вниманием и пониманием. Учащиеся с большим интересом стали относиться к "не
таким" (их определение) задачам, а позже и сами стали сочинять задачи с лишними
данными, предлагая их друг другу и учителю как на уроках, так и вне уроков.
Нам представляется, что этот интерес можно объяснить новой необычной
ситуацией в сфере знакомых вещей: для решения таких задач новых знаний не
требуется, но требуется новый подход к ним, новые мыслительные приёмы. Т.е.
происходит "шлифовка" мышления, его тренаж, что вполне соответствует запросам
растущего организма.
Был проведен эксперимент и в 10 классе той же школы, где на момент эксперимента
было 13 учащихся. Им была предложена для решения следующая текстовая задача:
в одной мензурке имеется некоторое количество кислоты, в другой мензурке – такое
же количество воды. Для приготовления раствора сначала вылили из первой
мензурки во вторую 30 граммов кислоты. Затем 2/3 раствора, получившегося во
второй мензурке перелили в первую. После этого в первой мензурке оказалось в
1,4 раза меньше жидкости, чем во второй мензурке. Сколько кислоты и воды было
взято первоначально?
Все 13 учеников смогли верно составить уравнение, провести его решение и
записать ответ: 12 граммов воды и кислоты было первоначально. На этом все
прекратили решение задачи. Далее им было предложено вернуться к условию
задачи, и попробовать подставить полученный результат в условие. Здесь сразу
же возникли трудности, поскольку из мензурки, содержащей 12 г жидкости,
требовалось вылить 30 г. Ученики отказывались понимать, как могло так
получиться, что задача красиво решилась, но то, что получили в качестве
ответа, не подходило по тексту задачи. Непонятным было также и то, как можно
записать в ответе, что нет решения, когда на самом деле оно есть.
Задача вызвала резко негативное отношение десятиклассников, которые считали
бесполезным решение таких задач для своего образования. Они требовали от
учителя предлагать им для решения "нормальные" задачи, какие им и придётся
решать при поступлении в ВУЗы.
Таким образом, эксперимент показал не только недостаточное развитие мышления
старшеклассников, но и то, что у них уже отсутствует стремление к такому
развитию. Они сами (полагаем, не без участия учителей) определили себе
"потолок" своего развития, своей образованности, что в принципе для человека
ненормально.
Аналогичный мини–эксперимент был проведён и в ходе преддипломной
педагогической практики в сентябре – октябре 1998 года. Он проводился с
учащимися средней школы № 2 г. Орши. В эксперименте принимали участие ученики
11–го класса, который является лицейским классом при Могилёвском
машиностроительном институте (выпускные экзамены по математике и физике в
этом классе совмещены со вступительными экзаменами в институт). Уровень
преподавания математики в этом классе достаточно высок (три ученика –
участники областной олимпиады по математике, один – её призёр).
Этим учащимся были предложены на уроке для самостоятельного решения следующие
задачи:
1.В параллелограмме стороны 3 см и 5 см, а высота 4 см. Найти площадь
параллелограмма.
2.В параллелограмме стороны 4 см и 5 см, а высота 3 см. Найти площадь
параллелограмма.
С первой задачей возникли проблемы следующего характера: часть учеников, не
обратив внимания на то, что в данной задаче параллелограмм определяется
однозначно (высота 4 см может быть проведена только к стороне 3 см), выдали два
ответа (12 см2 и 20 см2); ещё одна часть учеников
остановилась на одном решении, просто не рассмотрев возможный второй случай
(ответ либо 12 см2 либо 20 см2); и лишь один ученик
сначала задал вопрос о том, сколько решений может иметь задача, и, получив
совет "Думай!", выдал полное и правильное решение.
Со второй задачей у большей части учащихся дело обстояло практически так же,
т.е. большинство указало только один ответ (даже подсказка о том, что решений
может быть и больше, им не помогла), остальные – два ответа, но без
обоснований. И лишь один ученик (тот же, что решил и первую задачу) решил
самостоятельно и правильно эту задачу, выдав два ответа с аргументацией.
Как видим, результаты экспериментов показывают, что школьники не в состоянии
самостоятельно справиться с задачами указанных типов. Они не ставят перед
собой вопросов о переизбыточности, недостаточности или противоречивости
условий задач, не анализируют условие задачи, прежде чем начать её решение,
не возвращаются с полученным решением к началу задачи, чтобы проверить его.
Из чего можно заключить, что сформированность навыков решения математических
задач у учащихся средних школ (даже в специализированных классах) является
далеко не полной.
При целенаправленном использовании переопределённых задач ученики довольно
быстро приучаются анализировать условие задачи, но в первое время всё же
делают довольно грубые ошибки в решении, объясняющиеся прежде всего их
неумением проводить такой анализ. При решении задач переопределённых, но
имеющих в условии противоречие, ученики после небольшой тренировки находят
очевидные или слабо скрытые противоречия, но, если противоречие хоть
сколько–нибудь завуалировано, не замечают его и просто игнорируют вместо
того, чтобы вернуться к условию задачи и проверить решение. Т.е.
необходимость работы над задачей после получения ответа, необходимость
анализа этого ответа, выявление его соответствия тексту задачи формируются у
учащихся за более длительный срок и затратой больших усилий как самих
учащихся, так и учителя. Потому желательно начинать этот процесс намного
раньше, чем в десятом классе.
При решении задач неопределённых учащиеся не умеют перебирать всевозможные
случаи, которые возникают из–за этой неопределённости, и часто либо находят
одно решение, либо пишут, что задача не решается.
Итак, ответ на поставленный вопрос очевиден: сами учащиеся не готовы к решению
неопределённых и переопределённых задач, этому нужно их целенаправленно учить.
Как? Чтобы ответить на этот вопрос, сначала задумаемся о том, чему
могут научить задачи с «аномальным» условием?
II. Обоснование целесообразности задач с «аномальным» условием
Для ответа на последний вопрос рассмотрим исследуемые типы задач более подробно,
чтобы определить, что конкретно требуется от ученика при решении
каждого из них.
1. Неопределённые задачи – задачи с неполным условием, в котором для
получения конкретного ответа не хватает одной или нескольких величин или
каких–то указаний на свойства объекта или его связи с другими объектами.
Примеры:
1. В треугольнике одна сторона имеет длину 10 см, а другая 8 см. Найти
длину третьей стороны.
2. Поезд состоит из цистерн, товарных вагонов и платформ. Цистерн на 4
меньше, чем платформ, и на 8 меньше, чем вагонов. Какой длины поезд, если
каждая цистерна, вагон и платформа имеют длину 25 м?
3. Заасфальтировали на 30 км больше, чем осталось. Сколько процентов
дороги покрыто асфальтом?
С первого взгляда ясно, что задача 1 не может иметь решения, потому что в ней не
хватает данных. Однако исследуем ситуацию глубже. Вспомним неравенство
треугольника и запишем его для данного треугольника, обозначив неизвестную
сторону через а.
Получим:
10 + 8 > a;
a + 10 > 8;
a + 8 > 10;
а из этой системы следует, что
2 < a < 18.
Таким образом, нам удалось уточнить ответ с фразы "задачу невозможно решить"
до вполне определённого интервала, что следует признать ответом более
высокого уровня.
И во второй задаче напрашивается вывод, что никакой ответ там невозможен,
поскольку данных не хватает. Но при более внимательном анализе условия
выявляется, что не любое число может получиться в ответе. Например,
невозможны ответы 333 м и 250 м, хотя и по разным причинам. Первое
невозможно, потому что ответ должен быть кратным 25 м. А второе невозможно,
т.к. общее количество тяговых единиц не может быть равным десяти. Сколько же
этих единиц там может быть?
Если в поезде х цистерн, то платформ х+4, а
вагонов х+8. Вместе: 3х+12. Таким образом, всех
тяговых единиц не меньше пятнадцати, а возможный ответ: 25(3х+12)
м, где х – натуральное число. Над "дизайном" ответа можно
поработать, если переписать его так: 75(х+4). А теперь,
переобозначив буквой х (или другой) количество платформ, получим
самый короткий вариант ответа: 75х м, где х –
натуральное число, не меньшее пяти.
Что ни говори, а такое решение требует более высокого уровня умственной
деятельности, чем примитивное "Задача не имеет решения, потому что данных не
хватает". И, разумеется, что указанного решения от школьников сразу не
получишь, что и подтвердили первые пробы со стапроцентным результатом.
Третья из указанных здесь задач предлагалась девятиклассникам лицея. Результат
тот же: "Задача не решается...". Только дополнительная просьба назвать
несколько возможных ответов подтолкнула лицеистов к анализу и в конце концов
вывела на ответ, близкий к правильному: х%, где х
Î(50;100].
Вывод: решение неопределённой задачи обычно заканчивается
неопределённым ответом, в котором искомая величина может принимать значения из
некоего числового множества. Выявление этого множества и должно стать целью
решения такой задачи, что достигается вдумчивым анализом текста задачи и
взаимосвязей между данными величинами. Этому полезному для умственного развития
учащихся процессу нужно специально обучать.
Задачи этого типа требуют от ученика мобилизации практически всего набора
знаний, умения анализировать условие, строить математическую модель решения,
находить данные к задаче "между строк" условия. Практически, одной специально
подобранной задачей этого типа можно проверить знания ученика по целой теме. В
качестве такого примера можно рассматривать задачу: При каких значениях
положительного параметра a уравнение logax=ax будет иметь
единственное решение и указать его. Эта задача была предложена нашей
группе (группа «А» IV курса физико–математического Могилёвского университета,
1997 год) на занятиях по дидактике математики для самостоятельного решения, что
помогло студентам группы весьма существенно повторить и углубить знания по
широкому спектру школьного курса алгебры и начал анализа.
Вообще, уравнения и другие задачи с параметрами можно рассматривать как частные
случаи неопределённых задач. Проблемность перехода к таким задачам ощущают
учителя уже при переходе от уравнений 7х=12, 0х=3,
–5х=0, 0х=0 к линейному уравнению общего вида:
ах=b. Предварительная тренировка в решении неопределённых задач и здесь
была бы целесообразной и полезной.
2. Задачи переопределённые – задачи с избыточным составом условия, с
лишними данными, без которых ответ может быть получен, но которые в той или
иной мере маскируют путь решения.
Как уже показано выше, данные в таких задачах могут быть противоречивыми и
выявление этой противоречивости или непротиворечивости является обязательным
элементом решения такой задачи.
Например, в задаче "Найти площадь прямоугольного треугольника с катетами
9 см и 40 см и гипотенузой 41 см" мало найти ответ полупроизведением 9
на 40. Надо ещё выявить, будет ли у прямоугольного треугольника с катетами 9 см
и 40 см гипотенуза равной 41 см. Без этого выяснения решение задачи не может
быть признано полным.
В этом аспекте интерес представляют практические задачи. Например, при
изучении первой формулы площади треугольника учитель приносит в класс
вырезанный из бумаги треугольник с проведенными высотами и предлагает одному
из учащихся измерить длину какой–либо стороны, потом второму ученику длину
второй стороны, третьему – третьей, ещё трое измеряют высоты, каждый по
одной. Результаты измерений записываются на доске. Теперь учитель предлагает
вычислить площадь этого треугольника. Вопрос, какая высота к какой стороне
проведена, учитель переадресует учащимся, которые измеряли, но те,
естественно, не помнят, поскольку не фиксировали на этом внимания. Возникает
интересная проблема, которая в итоге всё же разрешается, исходя из того, что
площадь одного и того же треугольника не может иметь разных значений. Поэтому
самая большая высота должна быть проведена к самой маленькой стороне, а самая
маленькая к самой большой. Теперь площадь треугольника можно вычислять тремя
способами, но результат, как выясняется, получается не совсем одинаковым.
Появляется причина поговорить о сущности измерений, об их обязательной
неточности, о качестве приближённых измерений, об особенностях вычислений с
приближёнными числами и других соответствующих вопросах. И элементарная
задача на применение примитивной формулы наполняется богатым содержанием.
Задачи этого типа требуют от ученика умения анализировать условие, находить в
нём нужные данные и отбрасывать ненужные. Причём, "ненужными" у разных учеников
могут быть разные величины. Например, в задаче "Найти площадь
прямоугольника по стороне, диагонали и углу между диагоналями" одни
ученики будут искать ответ половиной произведения диагоналей на синус угла
между ними (тем самым сторона становится лишним данным), другие получат ответ
произведением сторон, предварительно вычислив вторую сторону по теореме
Пифагора (здесь угол становится лишним данным). Возможен и третий вариант,
когда лишним данным станет диагональ. Использование нескольких вариантов
решения такой задачи полезно не только для их сравнения, но больше для
самоконтроля: одинаковость ответов при разных решениях повышает уверенность в
их правильности. Отсюда можно получить и один из надёжных способов самоконтроля
в решении традиционных задач: после получения ответа вставить этот ответ в
текст задачи как одно из данных, а одну из известных величин считать
неизвестной и решить полученную новую задачу.
3. Нереальные (или противоречивые) задачи обычно относят к отдельному типу,
хотя, как отмечено выше, они являются составной частью переопределённых
(иногда определённых) задач.
Пример: Найти площадь треугольника со сторонами 10 см, 19 см и8 см.
Вовсе необязательно решать приведенную задачу, чтобы понять, что она не имеет
решения. Достаточно лишь проверить условие на противоречивость при помощи
неравенства треугольника и убедиться, что задача не может иметь решения.
Можно было бы решить эту задачу, используя формулу Герона, но и тогда в конце
концов был бы получен противоречивый результат (подкоренное выражение
получилось бы отрицательным).
Для таких задач характерным является то, что они могут иметь достаточно
красивое решение, как это было с приведённой выше задачей на переливание
жидкости, но только это решение будет противоречить здравому смыслу. При
решении таких задач необходимо всегда в конце возвращаться к условию и делать
проверку полученного решения. А поскольку противоречивость задачи не всегда
бросается в глаза, это приучит выполнять проверку полученного ответа в каждой
задаче. Некоторые из задач этого типа позволяют выявить противоречие данных
еще при анализе условия, в результате чего процесс решения становится
излишним. Достаточно частое повторение таких ситуаций приведёт учащихся к
необходимости анализировать условие перед началом решения, чтобы избавить
себя от лишней работы.
Итак, мы выяснили, что каждый из указанных типов задач несёт в себе
определённую развивающую функцию. Так, переопределённые задачи требуют умения
анализировать условие и строить решение задачи при помощи минимального числа
данных. Противоречивые задачи заставляют делать проверку решения, более
внимательно анализировать данные задачи. Неопределённые задачи требуют
достаточно обширных знаний об объекте задачи, о связях его с другими
математическими объектами, которые могут оказаться полезными при получении
пусть неопределённого, но всё же ограниченного некими рамками ответа.
Известно (см., например, книги Д.Пойа), что процесс решения математической
задачи предусматривает реализацию четырёх этапов: изучение текста задачи,
составление плана решения, его выполнение, изучение полученного решения
("взгляд назад"). Для успешного формирования у школьников умений, связанных с
реализацией того или иного вида деятельности, необходимо обучать их
самостоятельно выполнять каждый из указанных этапов процесса решения задач.
Для этого целесообразно учить учащихся операциям, соответствующим
определённому этапу работы с задачей. Указанные выше типы задач и позволяют
ученику усовершенствовать свои умения в каждом из данных видов деятельности.
III. Прикидка методического подхода
к обучению решению «аномальных» задач
Как же научить учащихся решать задачи указанных типов? Как приучить их к
"нестандартному"[1] подходу к решению
задачи?
Основой для ответа на поставленный вопрос можно считать известную таблицу
Д.Пойа "Как решать задачу" [16, с. 210-212]. В числе основных вопросов, над
которыми следует задумываться решателю, Д.Пойа выделяет следующие:
Возможно ли удовлетворить условию? Достаточно ли условие для определения
неизвестного? Или недостаточно? Или чрезмерно? Или противоречиво?..
Сохраните только часть условия, отбросив остальную часть: насколько
определённым окажется тогда неизвестное? Как оно сможет меняться?..
Все ли данные вами использованы? Все ли условия? Приняты ли во внимание все
существенные понятия, содержащиеся в задаче?..
Нельзя ли проверить результат? Нельзя ли проверить ход решения?..
Перечисленные выше вопросы и советы из таблицы Д.Пойа являются
малопопулярными или совсем непопулярными у школьных учителей. Хотя бы потому,
что первая часть этих вопросов и не требуется в отношении традиционных
школьных задач. Для того, чтобы таблица Д.Пойа заработала в полной мере, и
возникает необходимость дополнить школьные наборы задач задачами
неопределёнными и переопределёнными.
Попробуем осмыслить возможный методический подход к обучению учащихся решению
таких задач.
Начнём с того, что осторожное включение таких задач возможно уже в 5–6
классах или даже раньше [24, с. ]. Начинать, как нам представляется, следует
с введения задач переопределённых, предупреждая на первых порах учащихся о
наличии избыточных данных и предлагая им найти такие данные, постепенно
переходя от задач простых к таким задачам, в которых избыточные данные не
сразу бросаются в глаза. Когда учащиеся приобретут некоторые навыки решения
таких задач, можно перейти к введению таких задач уже без предупреждения о
наличии избыточных данных, чередуя эти задачи с традиционными определёнными
задачами. Таким образом, не зная, имеется ли в условии задачи лишнее данное
или нет, но подозревая, что оно может быть, учащиеся к каждой задаче будут
подходить критически, что вызовет большую, чем в традиционных условиях,
необходимость внимательного анализа условия задачи и различных подходов к её
решению.
На некотором этапе переопределённые задачи, предлагаемые учащимся, могут
стать противоречивыми. Использование таких задач постепенно приучит их к
тому, что обнаруженное в условии лишнее данное не следует игнорировать, но
следует проверять его на противоречивость (при этом, как нам представляется,
чаще нужно ориентироваться на вычисления с приближёнными величинами, чем с
точными). Кроме того, использование задач с противоречивыми данными позволит
учащимся заметить (не без помощи учителя) полезность вдумчивого анализа
условия, в результате которого можно выявить противоречивость и тем самым не
искать решения, т.е. облегчить себе работу. А поскольку никогда не ясно, есть
ли противоречие в условии задачи или нет, то вдумчивому анализу будут
подвергаться условия всех задач, что следует считать чрезвычайно полезным
качеством решателя задач.
Когда переопределённые задачи станут привычными и не будут вызывать у
учащихся настороженности и протеста, можно перейти к решению неопределённых
задач, снова же вначале предупреждая учащихся о том, что в условии задачи
некоторых данных не хватает, и предлагая им указать, каких. При этом полезно
сравнивать, как зависит ответ задачи от различных дополнений учащихся – с
возможным, но пока не обязательным, выходом на диапазон этого ответа. Ибо
целью решения таких задач, как уже отмечено выше, и является указание
диапазона возможных состояний ответа.
Мы попытались разработать систему задач с использованием всех задач
рассматриваемой классификации в одной из тем школьного курса геометрии.
Критерии создания такой системы задач рассматриваются в [19]. Автор пишет :
"Последовательное, постепенно усложняющееся варьирование условия задач
является основным принципом, определяющим построение упражнений при обучении
решению типовых задач. Вначале – на первоначальных этапах самостоятельного
решения новой для ученика типовой задачи (после того, как она разобрана в
классе) – варьирование условия касается самых несущественных его сторон,
непосредственно не влияющих на применение основного приёма решения, а именно
сюжета задачи и числовых величин. Последующее варьирование условия задачи
имеет целью не столько закрепление в памяти учащихся того или иного типового
приёма (это тоже необходимо), сколько выработку умения распознавать за
различной внешней формой задачи её одинаковую логическую структуру. На этом
этапе большое значение приобретает решение задач данного типа аналогичных по
логической структуре, но изменённых по словесной формулировке. При этом
изменение формулировки должно касаться той части условия, которая является
определяющей для выбора приёма решения.
Решая систему задач, построенную по этому принципу, учащиеся приучаются
улавливать самое существенное в условии задач, правильно абстрагируясь от
внешних сторон – своеобразия их формулировок.
На следующем этапе целесообразно вводить в условия задач дополнительные
элементы, увеличивая количество числовых данных. Исследования показывают, что
в этом случае, несмотря на то, что введение дополнительных данных никак не
влияет на использование основного приёма решения, для учащихся всё же
создаётся новая ситуация, требующая от них умения вычленить ту часть условия,
которая определяет применение типового приёма и в ходе действий при решении
задачи найти ему правильное место.
То же самое следует отметить и о применении задач переопределённых,
корректных, но вызывающих противоречие при решении. Эффект от введения этих
задач не стоит недооценивать, их цель в системе задач – вызов ситуации, при
которой задача не имеет решения при вроде бы существующем на самом деле
математическом (записываемом посредством математического языка) решении.
В дальнейшем уже можно прибегать к такому варьированию условий задачи,
которое требует видоизменения самого типового приёма. Такого рода
варьирование способствует выработке более сложных умений, значение которых
для формирования самостоятельного мышления учащихся очень велико. Речь идёт в
этих случаях о выработке умений перестраивать известные способы решения в
соответствии с изменением условий задачи. Успех этой перестройки
непосредственно зависит от того, в какой мере учащиеся умеют анализировать
задачи, улавливая одновременно и сходное и различное." [19, с. ]
И, наконец, последнее видоизменение условия задачи – составлять условие таким
образом, чтобы некоторых данных в них не хватало. С учётом предыдущего опыта
учеников по решению задач, этот тип задач, во–первых, будет для них несколько
сложным и новым, во–вторых, решая задачи такого типа, ученики более наглядно
осознают скрытые свойства объекта задачи, уясняют более детально динамические
соотношения между понятиями и определениями, применяемыми при решении данной
задачи.
IV. Расширенная система задач по теме «Сумма углов треугольника»
В соответствии с вышесказанным предлагается к рассмотрению система задач по
теме "Сумма углов треугольника" (геометрия, 7 класс). Тема эта не громоздкая,
достаточно чёткая и богато насыщенная различного рода задачными ситуациями.
Для составления требуемой системы задач было выделено 5 основных аспектов
данной темы:
· непосредственное использование указанного свойства углов в
произвольном треугольнике;
· то же – для равнобедренного треугольника;
· то же – для прямоугольного треугольника;
· то же – для углов, образованных внутри треугольника медианами,
биссектрисами, высотами и др.;
· то же – с выходом на внешние углы треугольника.
I. Применение свойства углов для произвольного треугольника
1. Два угла треугольника равны 26° и 118°. Найти величину третьего угла
треугольника.
2. Два угла треугольника равны 118° и 62°. Найти величину третьего угла.
3. Найти углы треугольника, если они пропорциональны числам 3, 4, 5.
4. В треугольнике ABC угол A равен 24°, угол C в два раза больше угла B.
Найти неизвестные углы треугольника.
5. Найти углы треугольника, если один из его углов равен сумме двух
других, а два меньших угла относятся, как 2:3.
6. Найти попарные отношения углов треугольника, если один из них равен
36°, а второй – 84°. (Задача имеет 6 ответов).
7. В треугольнике ABC угол A равен 30°, угол B равен 70°, и два угла
относятся, как 7:8. Найти углы треугольника ABC.
8. В треугольнике ABC угол A равен 30°, угол B равен 70°, и два угла
относятся, как 4:7. Найти углы треугольника ABC.
9. В треугольнике ABC угол A равен 30° и углы относятся, как 1:1:4. Найти
углы треугольника ABC.
10.В треугольнике ABC угол А равен 30°, и углы относятся как 1:2:6. Найти
углы треугольника ABC.
11.В треугольнике АВС угол А равен 70°, и два угла относятся как 5:6. Найти
углы треугольника АВС.
Первая задача традиционна для этой темы. Но вторая уже заставляет задуматься
о возможных границах ответов в таких задачах.
Шестая задача выводит на необходимость вариативных рассуждений, о чём
подсказка в скобках, тем самым готовит учащихся к вариативным рассуждениям в
следующей задаче. Для решения задачи 7 ученик должен сначала задуматься об
отношении каких именно углов идёт речь? Некоторые из этих вариантов будут
отброшены как противоречивые, но не сразу, а после необходимых вычислений.
Для ответа останется один из них. В задаче же 8 ни один из рассмотренных
вариантов не выведет на ответ. Аналогичные рассуждения понадобятся и при
решении задач 8–11.
II. Применение свойства углов для равнобедренного треугольника
1. Найти углы равнобедренного треугольника, если угол при его вершине
равен 28°.
2. Найти углы равнобедренного треугольника, если угол при его основании
равен 28°.
3. Может ли равнобедренный треугольник иметь углы величиной 55° и 70 °?
24° и 62°?
4. Найти углы равнобедренного треугольника, если один из них равен 100°.
5. Найти углы равнобедренного треугольника, если два его угла
соответственно равны: а) 55° и 70°; б) 40° и 110°; в) 20° и 20°; г) 60° и
60°.
6. Может ли биссектриса, медиана или высота треугольника разбивать его на
два равносторонних треугольника?
7. Найти углы равнобедренного треугольника, у которого высота, проведённая
к основанию, разбивает его на 2 треугольника так, что соотношение острых
углов каждого из полученных треугольников равно 1:2.
8. Доказать, что равнобедренный треугольник с углом 60° является
равносторонним.
9. Какими могут быть углы равнобедренного треугольника , если биссектриса
одного из углов разбивает треугольник на два равнобедренных треугольника.
10.Доказать, что если любые две биссектрисы треугольника, пересекаясь,
образуют со сторонами равнобедренные треугольники, то данный треугольник
равносторонний.
11.Доказать, что отрезки высот равностороннего треугольника образуют со
сторонами этого треугольника 3 равнобедренных треугольника.
Последние две задачи этого раздела – привычные задачи школьного учебника. Но
решать такие задачи ученики не любят именно потому, что здесь требуется
выполнить перебор всех возможных вариантов, к чему они не очень хорошо
подготовлены. Поэтому предыдущие задачи в большей своей части и содержат
необходимость выполнения перебора вариантов, что, как нам представляется, и
должно подготовить учащихся к решению двух последних задач.
III. Применение свойства углов для прямоугольного треугольника
1. Один из углов прямоугольного треугольника равен 73°. Найти другой его
острый угол.
2. В прямоугольном треугольнике один угол равен 65°. Найти величины
остальных углов.
3. Один из острых углов прямоугольного треугольника в 5 раз больше
другого. Найти эти углы.
4. Найти острые углы прямоугольного треугольника. если один из них на 32°
больше другого.
5. Острые углы прямоугольного треугольника пропорциональны числам 5 и 7.
Найти эти углы.
6. Разность острых углов прямоугольного треугольника равна 15°. Найти эти
углы.
7. Найти углы прямоугольного треугольника. если один из них в 5 раз больше
другого.
8. Найти углы прямоугольного треугольника, если один из них на 32° больше
другого.
9. Найти углы прямоугольного треугольника, если один из них в 3 раза
меньше другого.
10.Углы треугольника пропорциональны числам Х, 8 и 10. Каким может быть число
Х, если треугольник прямоугольный?
11.Два угла прямоугольного треугольника пропорциональны числам 2 и 3. Найти
углы треугольника.
12.Можно ли найти отношение сторон прямоугольного треугольника (хотя бы
некоторых), если известно, что один из его углов в 2 раза больше другого?
Первые шесть задач этого раздела традиционные. Пять следующих (от седьмой до
одиннадцатой) внешне похожи на первые шесть, но содержат одну
неопределённость, существенно влияющую на характер решения: речь уже не идёт
об острых углах и потому к числу затронутых в условии углов придётся теперь
относить и прямой угол. Таким образом, задача получит несколько возможных
ответов. Последняя задача не может быть решена в полном виде до изучения
теоремы Пифагора, поэтому в седьмом классе возможно лишь её частичное
решение: либо равнобедренный прямоугольный треугольник с отношением катетов
1:1, либо прямоугольный треугольник с углом 30°, где отношение катета к
гипотенузе равно 1:2.
IV. Применение свойства углов в треугольнике с дополнительными построениями
1. В треугольнике АВС биссектрисы углов А и В пересекаются в точке К.
Найти величину угла АКВ, если ÐА=50°, ÐВ=100°.
2. В равнобедренном треугольнике угол равен 68°. Под каким углом
пересекаются биссектрисы двух других его углов?
3. Под каким углом пересекаются биссектрисы равностороннего треугольника?
высоты равностороннего треугольника?
4. Треугольник имеет углы 36° и 74°. Под каким углом пересекаются высоты,
проведенные из вершин этих углов? Под каким углом пересекаются биссектрисы
этих углов?
5. В треугольнике АВС (АВ=ВС) проведена биссектриса СМ. Найти углы
треугольника АВС, если величина угла АМС равна 120°.
6. В треугольнике АВС ÐА=40°, ÐС=70°, биссектрисы углов А и С
пересекаются в точке К, ÐАКС=125°. Найти ÐВ.
7. В треугольнике АВС ÐА=30°, ÐС=80°, биссектрисы углов А и В
пересекаются в точке К, ÐАКВ=135°. Найти угол В.
8. Под каким углом пересекаются неравные биссектрисы равнобедренного
треугольника, один из углов которого 96°? 90°? 86°?
9. В равнобедренном треугольнике АВС проведена биссектриса АМ. Найти углы
треугольника АВС, если ÐАМС=64°.
10.Биссектрисы углов А и В треугольника АВС пересекаются в точке К. Найти
величину угла АКВ, если величина угла АСВ равна 170°.
11.Найти величину угла треугольника. если биссектрисы двух других его углов
пересекаются под углом 100°.
12.В каком треугольнике биссектрисы пересекаются под прямым углом?
13.В треугольнике АВС биссектрисы углов А и В пересекаются в точке К.
ÐBАC=70°. Найти угол АКВ.
В задачах этого раздела также запланирован переход от традиционных задач к
задачам, требующим анализа условия и рассмотрения различных вариантов.
V. Задачи с внешними углами треугольника
1. Внешний угол треугольника равен 130°, один из не смежных с ним
внутренних 70°. Найти углы треугольника.
2. Углы треугольника равны 47°, 69° и 64°. Найти внешние углы треугольника.
3. Внешний угол треугольника равен 130°, а два внутренних 60° и 70°. Найти
углы треугольника.
4. Внешний угол треугольника равен 130°, а два внутренних – 30° и 60°.
Найти углы треугольника.
5. Один из внутренних углов прямоугольного треугольника равен 47°, а один
из внешних – 137°. Найти величины остальных внутренних углов.
6. В прямоугольном треугольнике внутренний угол равен 47°, внешний 133°.
Найти величины остальных внутренних углов.
7. В прямоугольном треугольнике внутренний угол равен 47°, внешний 143°.
Найти величины остальных внутренних углов.
8. Найти углы равнобедренного треугольника. если один из его внешних углов
равен 30°.
9. Один из внешних углов прямоугольного треугольника равен 107°. Найти его
внутренние углы.
10.Один из внешних углов треугольника равен 130°, а один из внутренних – 46°.
Найти другие внутренние и внешние углы треугольника.
11.Один из внешних углов равнобедренного треугольника равен 96°. Найти
внутренние углы треугольника.
12.Сумма внешних углов с вершинами А и В равна 186°. Найти величину угла С
треугольника АВС.
13.Сумма двух внешних углов с вершинами А и В равна 172°. Найти величину угла
С треугольника АВС.
14.Внешний угол прямоугольного треугольника в 7 раз больше внутреннего с той
же вершиной. Найти углы треугольника.
15.Внешний угол прямоугольного треугольника в 4 раза больше внутреннего.
Найти углы треугольника.
16.Найти сумму внешних углов прямоугольного треугольника (по одному при
каждой вершине).
17.Разность двух внешних углов треугольника равна третьему внешнему углу.
Найти внутренние углы треугольника.
18.Найти отношение внешних углов равнобедренного треугольника, если отношение
его внутренних углов 2:5.
19.Под каким углом пересекаются две прямые, если при пересечении их третьей
сумма внутренних односторонних углов равна 215°?
20.Один из углов треугольника в 3 раза больше другого, а разность внешних
углов при этих же вершинах равна 80°. Найти углы треугольника.
21.Один из углов треугольника в 2 раза больше другого, а разность внешних
углов при этих же вершинах равна 80°. Найти углы треугольника.
22.Внешние углы треугольника пропорциональны числам 3, 7, 8. Каким числам
пропорциональны его внутренние углы?
23.Прямые a и b пересекаются под углом 85°. Прямая
c пересекает a и b так, что разность
внутренних односторонних углов равна 75°. Определить вид полученного
треугольника.
24.Прямые a и b пересекаются под углом 75°. Прямая
c пересекает a и b так, что разность
внутренних односторонних углов равна 85°. Определить вид полученного
треугольника.
25.Определить, под каким углом пересекаются прямые c и d
, если прямая а пересекает их так, что сумма внутренних
односторонних углов равна 54°.
26.Прямые k и l пересекаются под углом 33°. Прямая
р пересекает их так, что один из внутренних односторонних углов в 2 раза
больше другого. Найти углы треугольника, образованного этими прямыми.
27.Прямые a и b пересекаются под углом 40°. Прямая
р пересекает их так, что в получившемся треугольнике углы относятся, как
1:7:28. Найти углы треугольника, образованного этими прямыми.
28.Под каким углом пересекаются прямые c и d, если
прямая а пересекает их так, что разность внутренних
односторонних углов равна 90°
Из задач этого раздела остановимся на шести последних задачах. Возможные здесь
варианты появляются несколько неожиданно для учащихся. Например, в задаче 23
для построения прямой с возможны две ситуации (см. рисунки):
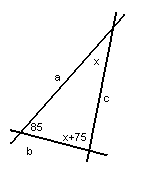 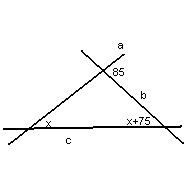
В этом случае имеем: 85°+х°+х°+75°=180° Здесь получаем: х=10°. | Возможно ещё и такое размещение прямых. 180°–85°+х°+х°+75°=180° х=5°. |
Задача имеет два ответа: 10° и 5°.
В задаче 24 также возможны два варианта построения прямых а,
b и с (см. рисунки):
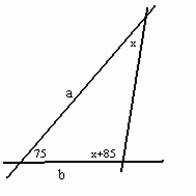 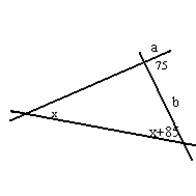
В данном случае имеем: 75°+х°+х°+85°=180°. Отсюда: х=10°. | Для такого размещения: 180°–75°+х°+х°+85°=180°. Отсюда: х=–5°, чего не может быть. |
Как видим, перестановка в условии задачи двух числовых данных (75° и 85°)
приводит к тому, что в ответе получается возможным лишь одно значение: х
=10°.
Вовсе необязательно предлагать эти задачи всем учащимся. Для учащихся с
преимущественной оценкой "3" многие задачи из второй части каждого раздела
недоступны и необязательны. В то же время для отлично успевающих учащихся
некоторые изначальные задачи очень просты и потому их можно пропускать. Из
предложенного перечня можно выделить набор задач, минимально необходимый для
оценки "3", потом – набор задач, минимально необходимый для оценки "4",
наконец – набор задач, минимально необходимый для оценки "5" (первый, второй
и третий уровни освоения указанной темы). Видимо, можно назвать задачи из
этого перечня, которые превышают и третий уровень, т.е. не являются
обязательными (но весьма желательными) для получения оценки "5".
Так, задачи первого уровня сложности рассчитаны на прямое применение
некоторого алгоритмического правила, а также применение этого правила с
небольшими вариациями. Задачи этого уровня не представляют сложности для
большинства учащихся, потому что подобных этим задач достаточно много решается
на уроках. Задачи неопределённые здесь не рекомендуются, а задачи
переопределённые допускаются в случае несложного выявления избыточных данных (о
наличии которых учащихся в большинстве случаев следует предупреждать).
Задачи второго уровня сложности могут иметь следующие отличительные черты:
· условие задачи избыточно, но не содержит противоречия и задача
решается однозначно. Для решения задач этого типа необходимо из всех данных
задачи выбрать необходимые, и применить их.
· условие задачи содержит противоречие (состав условия задачи может быть
как полным, так и избыточным).
· условие задачи не содержит никаких из рассмотренных нюансов с данными
(состав условия полный), но по сравнению с задачами первого уровня приём,
применяемый для решения, более сложный (правило применяется не "в лоб").
Задачи третьего уровня сложности отличаются ещё большим разнообразием.
Для решения задач этого уровня от учеников требуется и больший объём знаний
(при решении задачи приходится использовать комбинацию приёмов и навыков,
изученных раньше), и наличие навыка вариативных рассуждений, которого
теперешним ученикам в значительной мере не хватает. Задачи этого уровня
вдобавок к сложности приёмов решения могут иметь в условии неопределённость,
приводящую к неопределённому ответу.
Также стоит отдельно сказать несколько слов о задачах, которые по своей
сложности стоят выше задач третьего уровня. Эти задачи имеют в своём условии
неопределённость, но эта неопределённость подразумевает в решении задачи
бесконечное множество ответов. Чаще всего такая формулировка задачи пугает
ученика и он говорит, что задача не имеет решения, потому что не хватает
данных, хотя можно было бы провести решение данной задачи и получить довольно
конкретный результат.
Заключение
Подводя итог проделанной работе, отметим следующее.
О целесообразности введения неопределённых и переопределённых задач в
школьный курс обучения убедительно сказано авторитетными методистами,
специалистами в области математического образования. Инерционная школа пока
ещё не учитывает этой целесообразности, но сдвиги в указанном направлении уже
есть.
Бесспорно и то, что дополнение традиционных школьных наборов задач задачами
неопределёнными и переопределёнными (в работе использован обобщающий термин
для обоих видов задач – задачи с «аномальным» условием или просто
«аномальные» задачи) вызовет необходимость особых методических подходов к
обучению решению таких задач, подходов, расширяющих возможности учащихся в
решении задач вообще, углубляющих и усовершенствующих их навыки поиска
решения любой задачи, а в итоге развивающих их мышление. Попытки осознания
таких подходов предприняты в данной работе. На одном из примеров показан
возможный вариант расширения традиционного задачника, его дополнения задачами
с «аномальным» условием.
Разумеется, работа не может претендовать на полноту и завершённость,
поскольку затронутая проблема достаточно глубинна и объёмна и требует не
одного года кропотливой работы не одного человека.
Однако автор надеется, что хотя бы небольшой шаг в нужном направлении им сделан.
По материалам данного исследования подготовлена (в соавторстве) статья,
опубликованная в журнале «Матэматыка: праблемы выкладання» № 2 за 1999 год.
Список использованной литературы:
1. Атанасян Л.С. и др. Геометрия. Учебник для 7–9 классов средней школы. –
М.: Просвещение, 1990.
2. Буловацкий М.П. Разнообразить виды задач // Математика в школе. – 1988.
– № 5, с.
3. Булавацкі М., Макавецкі І. Аб задачах, якіх няма ў школьных падручніках
// Матэматыка: праблемы выкладання. – 1999. – № 2, с. 59 – 64.
4. Дегтянникова И.Н. Остроугольный или тупоугольный // Математика в школе.
– 1998. – № 5, с. 43.
5. Игнатенко В.З. Сюрпризы биссектрисы // Математика в школе. – 1998. – №
5, с. 42.
6. Каплан Б.С. Методы обучения математике. – Минск: Народная асвета, 1981.
7. Колмогоров А. Н . Математика - наука и профессия. – М.: Наука,1988.
8. Крупич В.И. Структура и логика процесса обучения математике в средней
школе.
9. Крутецкий В.А. Психология математических способностей школьников. – М.:
Просвещение, 1968.
10.Леонтьев А.Н. Проблемы развития психики. – М.: Издательство МГУ, 1962.
11.Математическое образование: современное состояние и перспективы (к
80–летию со дня рождения профессора А.А.Столяра): Тезисы докладов
международной конференции. – Могилёв: МГУ им. А.А.Кулешова, 1999.
12.Матюшкин А.М. Проблемные ситуации в мышлении и обучении. – М.: Педагогика,
1975.
13.Махмутов М.И. Проблемное обучение. – М.: Педагогика, 1975.
14.Метельский Н .В. Дидактика математики. Общая методика и её проблемы. –
Минск: Издательство БГУ, 1982.
15.Погорелов А.В. Геометрия 7–11. – М.: Просвещение, 1998.
16.Пойа Д. Как решать задачу. – Львов, 1991.
17.Пойа Д. Математическое открытие. – М.: Наука, 1976.
18.Рогановский Н.М. Геометрия 7–9. – Мн.: Народная асвета, 1997.
19.Самарин О.А. Очерки психологии ума. Особенности умственной деятельности
школьников. – М.: Издательство АПН, 1972.
20.Столяр А.А. Педагогика математики. – Минск: Вышэйшая школа, 1986.
21.Столяр А.А. Как математика ум в порядок приходит. – Минск: Вышэйшая школа,
1991.
22.Фридман Л.М. Психолого–педагогические основы обучения математике в школе:
– М.: Просвещение, 1983.
23.Фридман Л.М. Турецкий Е.Н. Как научиться решать задачи: – М.: Просвещение,
1989.
24.Эрдниев П.М. Преподавание математики в школе – М.: Просвещение, 1978.
25.Эсаулов А.Ф. Проблемы решения задач в науке и технике. – Л.: Издательство
Ленинградского университета, 1979.
Министерство образования Республики Беларусь
Могилёвский государственный университет им. А.Кулешова
кафедра методики преподавания математики
Дипломная работа
«Неопределённые и переопределённые задачи
(использование задач с «аномальным» условием
в процессе обучения математике)»
студента группы «А» V курса
физико–математического факультета
Маковецкого Ильи Ивановича
| Научный руководитель: Войтович Ф.С., старший преподаватель кафедры методики преподавания математики |
Могилёв 1999
[1] Слово "нестандартный" взято нами в
кавычки, поскольку мы считаем, что соответствующий подход к решению задач
должен стать стандартом для каждого ученика.
|

|