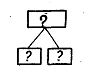
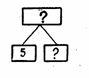
Курсовая: Педагогика в начальных классах

а также упражнения по преобразованию задач. Это, прежде всего, составление

задач, аналогичных решенной. Так, после решения задачи с величинами: ценой,

количеством и стоимостью – предложить составить и решить похожую задачу с

теми же величинами или с другими, например скоростью, временем и расстоянием.

Это составление задач по их решению, записанному как в виде отдельных

действий, так и в виде выражения, это составление и решение задач по их

краткой схематической записи (см. приложение 1).

Ученики называют величины, подбирают и называют соответствующие числовые

данные, формулируют вопрос и решают составленную задачу. Такую схематическую

запись можно выполнить на листе бумаги, причем название величин можно

записать на карточках и вставить их в верхнюю графу (цена, количество,

стоимость; масса одного предмета, число предметов, общая масса и др.). Можно

предлагать для составления задач краткую запись с числовыми данными или

рисунок. Позднее, после рассмотрения задач на пропорциональное деление

второго вида и задач на нахождение неизвестных по двум разностям можно

выполнить упражнения на преобразование задачи одного вида в другой, а после

их решения выполнить сравнение самих задач и решений этих задач.

Работа по ознакомлению с решением задач на пропорциональное деление второго

вида может быть проведена аналогично рассмотренной. При решении задач этого

вида ученики должны выполнять работу с большей долей самостоятельности,

поскольку эти задачи сходны с задачами ранее рассмотренного вида (их решение

отличается последними действиями: если ранее это было умножение, то здесь –

деление). Однако сходство задач приводит к ошибкам: некоторые ученики

смешивают решения этих задач, выполняя вместо деления умножение. Одним из

средств предупреждения таких ошибок служит решение пар задач различного вида

и последующее сравнение самих задач, а также их решений. Приведем пару таких

задач:

1) В столовую в первую неделю привезли 4 одинаковых мешка крупы, а во

вторую – 5 катких же мешков. Всего за эти две недели привезли 540 кг крупы.

Сколько килограммов крупы привезли в каждую неделю?

2) В столовую за две недели привезли 9 одинаковых мешков крупы. В первую

неделю привезли 240 кг крупы, а во вторую – 300 кг. Сколько мешков крупы

привезли в каждую неделю.

Записав каждую задачу кратко, ученики легко установят, в чем их сходство и в

чем различие. После решения этих задач дети должны установить сначала

сходство решений (обе задачи решаются четырьмя действиями, два первых

действия одинаковые), а затем – различие (в первой задаче два последних

действия – умножение, а во второй – деление). Заметим, что пары таких задач

включены в учебник.

До ознакомления с решением задач на нахождение неизвестных по двум

разностям важно предусмотреть специальные подготовительные упражнения, с

помощью которых раскрывается основная проблема задачи.

После подготовительных упражнений можно перейти к ознакомлению с решением

задач на нахождение неизвестных по двум разностям. Здесь, как и при

ознакомлении с задачами на пропорциональное деление, можно использовать

различные пути: можно сначала составить задачу на нахождение неизвестных по

двум разностям, преобразовав знакомую задачу на нахождение четвертого

пропорционального, а можно сразу предложить готовую задачу. В том и в другом

случае надо записать кратко в таблице или выполнить рисунок и после того

коллективного составления плана записать решение (лучше отдельными действиями

с пояснениями).

На этапе закрепления умения решать задачи на нахождение неизвестных по двум

разностям можно использовать упражнения аналогичные тем, которые предлагались

при решении задач на пропорциональное деление. После введения задач на

нахождение неизвестных по двум разностям второго вида.

По аналогичной методике следует провести работу по сравнению задач этих двух

видов и сравнению их решении. Полезны также упражнения по сравнению задач на

пропорциональное деле­ние и задач соответствующего вида на нахож­дение

неизвестных по двум разностям.

После того как в процессе решения про­стых задач ученики усвоят связи между

величинами: скоростью, временем и расстоя­нием, включаются составные задачи с

эти­ми величинами различной математической структуры, причем задачи этих

видов были введены ранее, но они включали другие величины (задачи на

нахождение суммы или разности двух произведений или двух част­ных, задачи на

нахождение четвертого пропорционального, на пропорциональное де­ление и др.).

Среди составных задач особое внимание должно быть уделено задачам на

встречное движение и в противоположных направлениях. Содержание этих задач

включает новый элемент: здесь представле­но совместное движение двух тел, что

требует специального рассмотрения.

До введения задач на встречное движе­ние важно провести соответствующую

под­готовительную работу. Надо познакомить с движением двух тел навстречу

друг другу. Такое движение могут продемонстрировать в классе вызванные

ученики. Например, два ученика-пешехода начинают двигаться одновременно от

двух противоположных стен навстречу друг другу, а при встрече

останав­ливаются. Ученики наблюдают, что расстоя­ние между пешеходами все

время умень­шалось, что, встретившись, они прошли все расстояние от стены до

стены и что каж­дый затратил на движение до встречи одинаковое время. Под

руководством учителя выполняется чертеж. Можно провести на­блюдение на улице

за движением автома­шин, пешеходов, велосипедистов и т. п. Рас­ширить

представления учащихся о встречном движении можно попутно с решением задач из

учебника. С по­мощью упражнений надо выяснить, что зна­чит «вышли

одновременно» пешеходы, авто­машины и т. п. и что при этом они были в пути до

встречи одинаковое время. Необходимо также, чтобы ученики твердо усвоили

связь между величинами: скоростью, временем и расстоя­нием при равномерном

движении, т. е. умели решать соответствующие простые задачи.

При ознакомлении с решением задач на встречное движение можно на одном уроке

ввести три взаимно обратные задачи. Сначала предложить задачу на нахождение

расстоя­ния, которое пройдут до встречи при одно­временном выходе пешеходы,

велосипедисты, поезда и т. п., если известны скорость каждого и время

движения до встречи.

Ознакомление с задачами на движение в противоположных направлениях может быть

проведено аналогично введению задач на встречное движение. Проводя

подготовитель­ную работу, надо, чтобы ученики пронаблю­дали движение двух тел

(пешеходов, авто­машин и т. п.) при одновременном их выхо­де из одного

пункта. Ученики должны заметить, что при таком движении расстоя­ние между

движущимися телами увеличи­вается. При этом надо показать, как вы­полняется

чертеж.

При ознакомлении с решением задач этого вида тоже можно на одном уроке решить

три взаимно обратные задачи, после чего выполнить сначала сравнение задач, а

затем их решении.

На этапе закрепления умения решать такие задачи ученики выполняют различ­ные

упражнения, как и в других случаях, в том числе проводят сравнение

соответ­ствующих задач на встречное движение и движение в противоположных

направлениях, а также сравнение решений этих задач. Эффективны на этом этапе

упражнения на составление различных задач на движение по данным в таблице

значениям величин и соответствующим выражениям.

В 3 классе ученики знакомятся с новым для них способом на нахождение

четвертого пропорционального – способом отношения. Поскольку математическая

структура этих задач знакома учащимся, то представляется возможность создать

при их решении проблемную ситуацию, а именно: предложить решить задачу уже

известным способом. В дальнейшем ученики решают задачи преимущественно

самостоятельно, причем при затруднении можно предложить им записать задачу

кратко. Разбор и здесь проводится с теми учащимися, которые сами не могут

решить задачу.

В программе по математике нет ограничений в отношении подбора задач, поэтому

учи­тель может по своему усмотрению включать задачи и другой математической

структуры. Вместе с тем надо учитывать основные требования программы в

отношении уровня умений решать текстовые арифметические задачи учащимися,

оканчивающими началь­ную школу: они должны приобрести твердые умения решать

простые арифметические за­дачи на все действия, а также должны уметь решать

несложные составные задачи в 2—3 действия.

При алгебраическом способе ответ на вопрос задачи находится в результате

составления решения уравнения.

При решении любой задачи алгебраическим способом после анализа содержания

задачи выбирается неизвестное, обозначается буквой, вводится в текст задачи,

а затем на основе выделенных в содержании задачи зависимостей составляются

два выражения, связанные отношением равенства, что позволяет записать

соответствующее уравнение. Найденные в результате решения уравнения корни

осмысливаются с точки зрения содержания задачи, а корни не соответствующие

условию задачи отбрасываются. Если буквой обозначено искомое, оставшиеся

корни могут сразу дать ответ на вопрос задачи. Если буквой обозначено

неизвестное, не являющееся искомым, то искомое находится на основе

взаимосвязей его с тем неизвестным, которое было обозначено буквой.

В начальном курсе обучения дети также знакомятся с графическим способом.

Опираясь только на чертеж легко дать ответ на вопрос задачи. Иногда решение

задачи графическим способом связано не только с построением отрезков, но и с

измерением их длин.

При обучении решению текстовых задач необходимо достигнуть двух

взаимосвязан­ных целей — обучить: 1) решению опре­деленных видов задач; 2)

приемам поиска решения любой задачи. Первая из них важна потому, что дает

необходимый опыт и возможность выделить в решаемой задаче те подзадачи,

решение которых известно. Кроме того, при решении каждой новой задачи можно

использовать те спосо­бы и приемы, которые давали прежде положительные

результаты. Но на практике приходится встречаться с задачами, при поиске

решения которых никакой прежний опыт не помогает и требуется догадка,

«открытие». Можно ли помочь ученику прийти к такой догадке, дать ему

неко­торое средство, помогающее «открытию?» При реализации идей развивающего

обу­чения такая цель представляется даже более важной, так как помогает

развитию таких когнитивных способностей, как умение проанализировать новую

ситуацию, на основе проведенного анализа принять правиль­ное решение,

выработать план действий и суметь осуществить его.

Для того чтобы решить поставленную задачу, необходимо построить ее

математическую модель, а затем применить известные методы для нахож­дения

числового значения искомых величин. При этом основная трудность как раз и

состоит в переходе от текста к математи­ческой модели. Для построения

математи­ческой модели необходимо, прежде всего, реконструировать в

воображаемом внутрен­нем плане описываемую в задаче си­туацию, затем выделить

в ней существен­ные признаки и абстрагироваться от всего того, что является

несущественным с точки зрения поиска ответа на поставленный вопрос. Например:

«Купец купил 138 аршин черного и синего сукна за 540 р. Спрашивается, сколько

аршин того и другого сукна купил купец, если синее сукно стоило 5 р. за

аршин, а черное — 3 р. за аршин?» Сначала он пытается разделить 540 на 138,

затем 540 на 5 и т. п.

Существенным является то, что речь идет о купце, о сукне синего и черного

цвета. Поэтому задача не изменится, если ее сформули­ровать так: куплено два

сорта материи по цене 3 р. и 5 р. за метр. Сколько куп­лено материи каждого

сорта, если всего было куплено 138 м, а вся покупка стоила 540 р.?

Несущественным является и то, что речь идет о некоторой коммерческой

опе­рации. Задачу можно было бы сформу­лировать и так: из 540 м материи сшили

138 платьев и блузок. Сколько сшили платьев и сколько блузок, если известно,

что на платье расходовали по 5 м ткани, а на блузку — по 3 м?

Что же существенно? То, что в задаче рассматриваются величины, связанные

пря­мой пропорциональной зависимостью: коли­чество купленной материи и ее

стоимость (количество сшитых изделий и израсходо­ванная ткань); то, что

известна стоимость покупки (количество затраченной ткани), це­на каждого вида

материи (норма расхода на каждый вид изделия), количество всей купленной

материи (вся израсходованная ткань); то, что неизвестно, сколько материи

каждого вида куплено (сколько изделий каждого вида сшито).

Для поиска решения необходимо вы­явить зависимости между указанны­ми

величинами. Согласно существующей методике это делается с помощью некото­рого

рассуждения. Но, как показывает практика, подобное рассуждение трудно

воспринимается младшими школьниками. Возникает вопрос, как провести

необходи­мое для поиска решения задачи рассуж­дение наиболее доступным

младшему школь­нику образом. Для этого можно предста­вить всю существенно

важную информа­цию в наглядной и легко обозримой форме — в виде картинки, т.

е. построить некоторую промежуточную графическую модель.

Почему предпочтение отдается графиче­ским методам? Графическая информация

легче для восприятия, более емкая (лю­бой рисунок достаточно долго пришлось

бы описывать словами), и, вместе с тем, может быть достаточно условной.

Требования, предъявляемые к графиче­ской модели предметной области задачи,

можно сформулировать так. Она должна:

— «опредмечивать» абстрактные поня­тия;

— нести информацию лишь о существен­ных признаках задачи;

— давать возможность непосредственно усматривать зависимость между

величинами, о которых идет речь в задаче;

— допускать ее практические преобразо­вания;

— строиться на основании анализа тек­ста задачи;

— не предъявлять неумеренных требований к графическим навыкам учащихся.

Рисование графической схемы, во-первых, (вставляет ученика внимательно читать

текст задачи, во-вторых, позволяет перенести часть умственных действий в

действия практические и закрепить результат в виде ма­териального объекта, в-

третьих, дает возможность искать решение самостоятельно.

Рассмотрим задачу: «В колхозе 40 автомашин – легковых и грузовых, причем на

каждую легковую машину приходится четыре грузовые. Сколько легковых и сколько

грузовых машин в колхозе?» Изобразим каждую машину палочкой (40 машин – 40

палочек) известно, что на каждую легковую машину приводится 4 грузовые.

Поэтому отложим одну палочку – это легковая машина. Под ней положим 4 палочки

– это 4 грузовые машины. Будем поступать так до тех пор, пока все 40 палочек

не окажутся разложены. Чтобы ответить на вопрос задачи, достаточно сосчитать,

сколько палочек положено в верхнем ряду и сколько палочек положено в нижнем

ряду. Такое решение задачи можно назвать практическим. Это еще один из

способов решения текстовых задач.

Обучение детей решению задач разными способами важно. Эта работа развивает

логическое мышление, интерес к уроку математики.

1.3. Особенности работы над задачами по системе Л.В. Занкова.

Начальная школа все дальше и дальше уходит от традиционной методики

математики. Появ­ляются различные типы школ, вводятся аль­тернативные

программы и учебники.

Наиболее распространенной среди альтерна­тивных систем является дидактическая

система, разработанная под руководством академика Л. В. Занкова. Эту систему

учитель выбирает не только потому, что она привлекает своими прин­ципами:

обучение должно вестись на высоком уровне трудности, в быстром темпе; ведущая

роль в обучении математике отводится теории, причем теоретические знания

тесно связаны с обязатель­ным осознанием учащимися процесса обучения.

Однако наблюдение за работой учителя, анализ результатов самостоятельных и

кон­трольных работ говорит о том, что именно эти принципы в практике обучения

реализуются недостаточно полно.

Прежде всего настораживает то, что зачас­тую наряду с учебниками математики

И. Н. Аргинской на партах лежат и учебники М. И. Моро и др.

Конечно, творчески работающий учитель никогда не ограничится одним учебником,

а бу­дет стремиться использовать все богатство за­даний других пособий,

методических приемов, выбирая то, что наиболее подходит именно для его

учеников. И с этим нельзя не согласиться.

Однако учитель должен задуматься и над тем, что обучение учащихся по двум

учебни­кам, сильно отличающимся как содержанием, так и методическими подходами,

формализм и по­верхностное изучение материала, приводит к перегрузке учащихся.

Особенно это заметно при обучении решению текстовых задач, ибо, как показывает

практика, именно здесь у учи­теля и учащихся возникают затруднения.

Это порождает крайне неверное мнение, что по системе Л. В. Занкова могут

обучаться лишь избранные дети и работать избранные учителя.

Не будем утверждать или дискутировать о том, усваивают или не усваивают дети

материал (известно, что методическая система Л. В. Занкова зарекомендовала

себя и доказала высокую эффек­тивность усвоения математических знаний и

раз­вития мышления учащихся), как и то, все или не все учителя смогут

работать по данной системе.

Хотелось бы обратить внимание на то, что значительному большинству учителей

(да­же тем, кто прослушал курс переподготовки, где рассматривались и

раскрывались принци­пы обучения, приемы и методы работы) нужна основательная

помощь, которая заключалась бы в конкретизации методических приемов и методов

работы, ибо отсутствие таковых при­водит к противоречию между предлагаемыми

принципами и их реализацией в практике.

Попытаемся проанали­зировать некоторые затруднения, возникаю­щие у учителя и

Алгебраический метод решения задач вво­дится с I класса и уже к III

классу становится основным методом решения. Как известно,

ал­гебраический метод решения задач развивает теоретическое мышление,

способность к обоб­щению, формирует абстрактное мышление и, кроме того,

обладает такими преимуществами, как краткость записи и рассуждений при

со­ставлении уравнений, экономит время. Видимо, эти преимущества и привели к

тому, что значи­тельная часть учителей отдает предпочтение при решении задач

алгебраическому методу.

Однако существует и другое мнение о том, что арифметический метод решения

задач развивает мышление не в меньшей степени, так как ученику необходимо

разбить состав­ную задачу на простые и на основе логически строгих рассуждении

в определенной последо­вательности решить их. Арифметический спо­соб решения

требует большего умственного напряжения, что положительно сказывается на

развитии умственных способностей, матема­тической интуиции, на формировании

умения предвидеть реальную жизненную ситуацию. Именно поэтому

полноправным методом решения задач в начальных классах.

Следует отметить, что арифметический способ решения доступен не всем учащимся

так как мышление младшего школьника ноет наглядно-образный характер.

Конкретное мышление младших школьников проявляется е том, что они могут

успешно решить ту или иную задачу в том случае, если опираются не действия с

реальными предметами. Поэтому для осознанного выбора действия, посредст­вом

которого решается задача, необходимо ил­люстрировать задачную ситуацию, чтобы

уча­щиеся осознали, почему и зачем выполняется то или иное действие.

Работу по формированию умения решать задачи "на предположение" арифметическим

способом целесообразно начинать с первых задач, включенных в учебник

математики, так как они содержат небольшие данные и задач­ную ситуацию можно

легко проиллюстриро­вать.

Особого внимания и творческого подхода требуют задачи, предлагаемые в конце

учебника. Именно на данном этапе обучения должно проявляться умение

применять различные приемы и методы решения задач, умение анализировать,

рассуждать, предлагать и проверять эти предположения, делать соответствующие

выводы. Поэтому при решении задач учителю необходимо организовать работу таким

образом, чтобы учащиеся находили различные способы решения, сравнивали их и

выбирали наиболее легкий и рациональный.

Однако значительная часть учителей, сле­дуя указаниям, предложенным к данной

зада­че, проводит работу над задачей, которая недо­статочно полно реализует

как обучающие, так и развивающие функции.

Чтобы усилить развивающий аспект обуче­ния, полезно решить задачу

арифметическим способом. Осознать выбор действий, посред­ством которых

решается задача, поможет пра­вильно выбранная наглядная интерпретация задачи.

Метод перебора при решении задач оказыва­ет положительное влияние на развитие

мышления учащихся, так как выбор предполагаемого ответа, соотнесение этого

данного с условием задачи помогает осмыслению связей и зависи­мостей между

величинами, входящими в задачу, развивает умение предвидеть, вырабатывает

интуицию и последовательность рассуждении.

При сравнении способов решения выясня­ется, что одни учащиеся отдали

предпочтение арифметическому способу, другие – по способу подбора. Тем не

менее систематическая работа по решению задач разными способами, сравнение

решений и их обсуждение, выбор рационального дает возможность лучше осознать

связи и зависимости между величинами, формирует умение рассуждать, делать

выводы и обосновывать их.

Все сказанное дает основание предполагать, что затруднения возникающие у

учителя в процессе работы порождают мнение о том, что по данной системе

развивающего обучения могут работать лишь избранные учителя. Однако это не

так.

Учителю нужны методическая помощь, методические разработки и рекомендации,

которые позволили бы сэкономить время на подготовку к уроку, сохранить

уверенность, силу и энергию, необходимую для плодотворной и творческой

работы.

1.4. Как составить и решить задачу по системе Д.Б. Эльконина – В.В. Давыдова.

Начнем с очень простого, на первый взгляд, вопроса: "Что такое задача?" Или

"Как узнать задачу?" Дети обязательно скажут: "Это там, где слова", ''Задача

- это вопрос", "В ней обязательно что-то происходит". Правда, у нас очень

умные дети? Тогда предложите им выбрать из предложенных записей задачу:

1. На склад привезли 3 т картофеля.

2. Сколько цветов в букете?

3. На празднике было 20 красных шаров, 10 зеленых и 15 синих. Сколько всей

шаров было на празднике?

4. На сколько ящик массой 15 кг тяжелее ящика массой 8 кг?

5. В вазе 5 яблок и 7 груш. Найди общее количество фруктов.

С пунктами 1 и 2 не возникает пробле­мы, так как в первом нет вопроса, а во

вто­ром нет данных ("ничего неизвестно"). Текст под номером 3 позволяет

сформулировав основные элементы задачи - условие и воп­рос. А дальше, не

давая детям опомниться вычеркнем тексты под номером 4 ("в нем нет условия") и

номера 5 ("нет вопроса") и попросите оценить ваши действия. При внимательном

рассмотрении окажется, что ус­ловие и вопрос задачи могут быть

сформу­лированы в одном вопросительном предло­жении, а бывает и так, то

вопрос "спрятан" в указание совершить какие-либо действия. Итак, казалось бы,

простой вопрос о задаче открывает целую серию исследовательских уроков. Они

будут продолжены по мере на­копления возможных оснований для сравне­ния и

классификации задач. Завершить дан­ный урок можно открытием "маленькой

тай­ны" (чем успокоим того ребенка, которого в задаче пока волнуют только

действующие лица): задача имеет сюжет. Это слово может стать вашим "подарком"

детям, а так как при­нято благодарить за презент, попросите ре­бят придумать

разные задачки на какую-либо тему (тему дети могут выбрать сами).

Чтобы избавиться от "текстового страха", поставим перед собой первую задачу:

научиться читать так, чтобы ви­деть за скорлупой слов математическое ядро. В

схеме решения зада­чи появляется первый шаг: "Читаю задачу". Для учителя не

является секретом, что текст читается дважды: цель первого прочтения -общее

знакомство с задачей, второго - структурирование текста с помощью логических

пауз, выделения голосом данных. Наш пер­вый шаг относится к первому чтению

задачи. Как же зафиксиро­вать на бумаге результат второго? Если мы сумеем

научить этому наших детей, то можно смело утверждать: половина проблем в

ре­шении задач снята!

По моему убеждению, каждый ученик должен "понимать", то есть уметь

обрабатывать текст задачи.

Итак, выделив математическое ядро, читаем ее второй раз и ставим перед со­бой

очень важную задачу: выделение величин и отно­шений между ними, которые

заключены, как говорят дети, "в главных словах и числах (буквах)". Это второй

шаг в решении любой задачи.

Можно с ребятами договориться подчеркивать эти слова карандашом в книге и

цветным мелом на доске. Вопрос задачи всегда выделяем особо - это цель наших

действий. Вот что получается:

Трусливый охотник перед охотой подкрепился двумя булочка­ми, но

истратил охотник булочками на поддержку своих сил?

Текст уже не пугает; зрительно делается акцент на выделенные слова, а их

стало во много раз меньше. Многие дети вздохнули с облегчением: "Задача-то -

проще не бывает". Но "расслабиться" нам не дал ученик, которому математика

дается труднее, чем остальным, и этот факт, как это ни парадоксально,

помогает всем ос­тальным более осознанно выполнять свои действия (как в

поговор­ке "Не было бы счастья, да несчастье помогло"). Его вопрос: "Ре­бята,

и все-таки, как узнать в тексте главные слова?" - слегка поубавил радость от

кажущейся легкости. Этот ученик задал самый главный вопрос урока, заставив

отрефлексировать способ действия. И не оказалось такого ученика, его роль

должны взять на себя вы и попросить детей обсудить, по како­му признаку они

выделяют величины.

Первое, что предложили ученики, - это проверить, правильно ли в данной задаче

они выделили слова. Ход был гениально про­стой: стереть с доски все слова,

кроме выделенных. Получилось следующее:

...двумя булочками ... тремя булочками ... двумя булочками.

Сколько всего булочек?

Исключение части слов не повлияло на математическую мо­дель задачи, то есть

мы совершенно безболезненно можем понять, а следовательно, решить данную

задачу. Немного погодя у нас родился второй способ выделения величин: не

подчеркивание важ­ных слов, а удаление несущественных (обратите внимание:

дети сами нашли для себя более простой метод - метод исключения). Ученики

подтолкнули меня к созданию нового вида заданий: каждая группа получает свой

текст задачи; надо закрасить маркером все слова, оставив только важные.

Соблюдается условие: текст с закрашенными словами передается по кругу другой

группе, кото­рая должна будет понять и решить задачу. Критерием правильности

выступает возможность восстановления математической моде­ли (не сюжетной!).

В процессе обсуждения выясняем, что выделять следует составные: числа (буквы)

и наименование при них; действующие лица там, где есть сравнение; слова,

указывающие на действия. Последнее указание надо тоже изучить подробно.

Хочу заметить, что процесс обработки текста важен не только в решении задач.

Существует у учеников еще один любимый "штамп": "Я не понял задание". А что

это значит? Казалось бы текст написан по-русски, чего же тут не понять?

Проблема в том, что его нужно "перевести" с русского на математический язык и

наоборот. Ребенок не выделяет для себя понятие, не видит указа­ний на

совершение действий.

Итак, начав с решения простейшей задачи для первого класса, мы с вами

столкнулись с более значимой проблемой - проблемой текста в математике.

Каждый новый ответ в решении этой пробле­мы порождает несколько новых

вопросов.

Мы прошли нелегкий путь знакомства с математическим текстом, а также важным

шагом выделения величин. Познакомимся со следующими шагами:

3. Фиксирую условие схемы.

4. Пишу формулы.

5. Вычисляю, записываю ответ.

6. Возвращаюсь к тексту задачи, делаю проверку.

Причем такие важные моменты, как фиксация условия задачи схемы, запись

формулы и вычисление с записью ответа, следует рассматривать в комплексе.

Для того чтобы увидеть, действительно ли ребенок уме­ет соотнести текст и

схему, удобно воспользоваться обрат­ной задачей: не по тексту изобразить

схему, а по схеме вос­становить текст.

На уроках контроля можно предложить проверить, правильно ли составлена схема

по задаче. В этом случае можно вос­пользоваться приемом, предложенным Э.И.

Александровой для установления взаимнооднозначного соответствия, - это

проведение "дорожек" от слова к его изображению в схеме.

Для формирования действия контроля за результатом отлично подходят задачи,

содержащие несколько вопросов или задачи, в которых идет указание на поиск

нескольких величин словами "Найдите каждый.". Последний шаг – это оценка

правдоподобности результата.

Действие оценки можно выделить в самостоятельные задания, которые могут

звучать так: "Прочитав задачу, исключи те варианты ответов, которые

противоречат сюжету", "Выбери те ва­рианты, которые могут появиться в

ре­зультате".

Отдельно следует рассматривать чи­сто математическую прикидку, которая будет

зависеть от модели задачи. Чаще всего она заключается в со­отнесении частей и

целого, проверке ис­пользования различных величин в одном действии, а так­же

в проверке используемых мер или наименований.

2. Практическая часть.

Учитель должен на практике руководствоваться теоретическими основами. Теория

и практика неразрывно связана между собой и не могут существовать друг без

друга. Рассмотрев и ознакомившись с теоретической основой решения задач,

хотела бы полученные знания на практике. То есть рассмотреть, как лучше

поставить вопрос к задаче, сделать краткую запись, как проанализировать

задачу, каким способом легче решить задачу. А также рассмотреть задачи

решаемые в третьем классе: задачи на увеличение (уменьшение) числа на

несколько единиц, сформированные в косвенной форме; задачи на

пропорциональное деление, задачи на нахождение неизвестных по двум разностям,

задачи на встречное движение и в противоположных направлениях и другие.

При анализе задачи от вопроса и от числовых данных можно выделить несколько

этапов, достигнуть которые можно путем решения простых задач:

1. В одной стопке были несколько тетрадей и в другой стопке были тетради.

Сколько тетрадей в двух стопках?

2. На одной тарелке лежало б яблок и на другой лежало несколько яблок.

Сколько яблок лежало на двух тарелках?

3. На одном кусте 4 помидора, а на дру­гом 5. Сколько всего помидоров на двух

кустах?

Рассматривается первая задача. Ведется беседа:

— Условимся, что при анализе вопрос задачи будем обозначать прямоугольником

со знаком вопроса. Чтобы дать ответ на вопрос задачи, что надо знать?

(Сколько было тетрадей в первой стопке и сколько во второй.)

В прямоугольнике ставим знак вопроса — вопрос задачи. От этого прямоугольника

проведем два отрезка и начертим два „других прямоугольника. Поскольку этих

чисел в за­даче не дано, то в прямоугольниках ставим знаки вопроса (рис. 1).

Рассматривается вторая задача. Учитель чертит на доске схему (рис. 2),

сопровождая беседой:

рис. 1 рис. 2

— Чтобы ответить на вопрос задачи, какие числа нам надо знать? (Сколько яблок

лежало на каждой тарелке.)

— На первой тарелке лежало 5 яблок, поэтому в одном прямоугольнике пишем

число 5. Сколько яблок было на второй тарелке, в задаче не сказано, поэтому

во втором прямоугольнике ставим знак вопроса.

Учащиеся убеждаются в том, что и вторую задачу решить нельзя.

Наконец, рассматривается третья задача. Учитель чертит на доске схему (рис.

3) и ведет беседу.

— Чтобы ответить на вопрос третьей задачи, что нам надо знать? (Сколько

помидоров было на первом и втором кустах.)

— Можем мы эту задачу решить? (Да, можем.)

— Что мы запишем в прямоугольниках? (В одном запишем число 4, а в другом —

число 5.)

После этого учащиеся должны повторить рассуждение в связной форме: чтобы

ответить на вопрос задачи, надо знать, сколько помидоров было на первом кусте

и сколько помидоров было на втором кусте. Оба эти числа нам известны. Чтобы

решить задачу, надо к 4 прибавить 5, получится 9. Ответ 9 помидоров.

Затем решаются задачи в два и в три действия: «Отец и сын окапывали кусты

смородины. Отец в час окапывал 5 кустов, а сын 3. Сколько времени они должны

работать вместе, чтобы окопать 24 куста?» После уяснения и сокращения записи

условия задачи учащиеся под руковод­ством учителя разбирают ее подобно тому,

как разбирали простые задачи. Затем ведется фронтальная беседа:

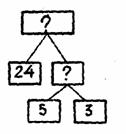
— Вопрос задачи обозначим знаком вопро­са, записанным в прямоугольнике (рис. 4).

рис. 4

Чтобы ответить на него, какие два числа надо знать? (Сколько кустов надо

окопать (24 к.) и сколько кустов окапывали вместе за час отец и сын.)

— От прямоугольника со знаком вопроса на одну клетку ниже чертим два других

прямоугольника. Что мы в них запишем? (В одном запишем число 24, а в другом

поставим знак вопроса, так как неизвестно, сколько в час окапывали кустов

отец и сын вместе.)

— Чтобы узнать, сколько в час окапывают кустов отец и сын вместе, что надо

знать? (Сколько отдельно кустов окапывает отец — 5 к. и сын — 3 к.)

— От прямоугольника со знаком вопроса на одну клетку ниже начертим еще два

прямоугольника. Что мы в них запишем? (В одном запишем число 5 — количество

кустов, окапываемых в час отцом, а в другом число 3 — количество кустов,

окапываемых в час сыном.)

После фронтального анализа учащиеся повторяют рассуждение в связной форме:

чтобы ответить на вопрос задачи, надо знать, сколько кустов надо окопать (24

к.) и сколько кустов в час окапывают вместе отец и сын. Для этого надо знать,

сколько кустов отдельно окапывает в час отец (5 к.) и сколько кустов

окапывает в час сын (Зк.) В первом вопросе узнаем, сколько кустов вместе

окапывают в час отец и сын, в втором — сколько времени они окапывали.

Если разбор этой задачи ведется с числовых данных, то он сопровождаете беседой:

— Если отец в час окапывает 5 кустов, а сын 3 куста, то что можно узнать?

(Сколы кустов в час они окапывают вместе.)

— Зная это и то, что им надо окопа 24 куста, что можно узнать? (Сколь

времени, они должны работать вместе)

Далее решаются задачи в 4 и в 5 действий:

«Птицефабрика должна отправить в магазины 6000 яиц. Она уже отправила 10

ящиков по 350 яиц и 4 ящика по 150 яиц. Сколько яиц осталось отправить в

магазины?»

Записывая сокращенно условие задачи с использованием числовых выражений,

ве­дем рассуждение: если было 10 ящиков по 350 яиц в каждом, то яиц было

350·10. Отпра­вила также 4 ящика по 150 яиц, это составляет (150·4) яиц.

Отправили: (350·10) яиц

(150· 4) яиц 6000 яиц

Страницы: 1, 2, 3