Курсовая: Педагогика в начальных классах

Осталось ?

Выполняя неполный анализ от вопроса, учащиеся рассуждают примерно так: «Чтобы

ответить на вопрос задачи, надо знать, сколько всего яиц надо отправить (6000

яиц) и сколько яиц птице­фабрика уже отправила. Чтобы узнать, сколько яиц

фабрика отправила, надо знать, сколько она отправила в первый и во второй

раз. В первом вопросе узнаем, сколько птицефабрика отправила яиц в 10 ящиках,

во втором — сколько она отправила яиц в 4 ящи­ках, в третьем —сколько всего

яиц птице­фабрика отправила и в четвертом — сколько яиц осталось отправить.

Схемы полного анализа (рис. 5) и неполного (рис. 6) нагляд­но показывают'

преимущество и недостатки каждого из них.

Учащиеся, умеющие составлять план реше­ния задачи, самостоятельно записывают

решение по указанию учителя или в форме математического выражения, или по

отдельным действиям.

Используя прием сравнения приведем пример решения задачи:

1) Нужно покрасить 150 рам. Один маляр может это сделать за 15 дней, а другой

— за 10 дней. За сколько дней выполнят эту работу оба маляра, если будут

работать вместе?

2) Библиотеке нужно переплести 1 500 книг. Одна мастерская может переплести

эти книги за 15 дней, а другая — за 10. За сколько дней закончат работу эти

мастерские, работая вместе?

Решение этих задач вызывает трудность у учащихся и поэтому традиционный поиск

решения проводится под руководством учите­ля. Сначала ученики называют

величины и записывают задачу кратко в виде таблицы.

Красили в день	Время работы	Всего покрасили рам
? ?	15 дн.	150
?	10 дн.	150

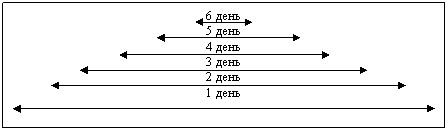
Затем, опираясь на записи в таблице, проводится разбор задачи, чаще всего от

данных к вопросу, так как разбор задачи от вопроса вызывает затруднения у

учащихся, а подобная краткая запись не помогает, а скорее тормозит поиск

решения задачи. Действительно, знак фигурной скобки на­правляет на ложный

путь выбора первого действия, так как дети прочно усвоили смысл этого знака,

как суммы, как объединения множеств. И поэтому на вопрос: «Что нужно знать,

чтобы ответить на вопрос задачи?» — довольно часто можно услышать ответ:

«Нужно найти, сколько всего дней они работали».

Первую задачу решаем коллективно с подробным анализом, а вторую предлагаем

для самостоятельного решения. Опишем работу над задачей, прово­димой на

уроке. Учитель просит ответить на вопросы: сколько всего рам должен был

покрасить маляр? За сколько дней может это сделать первый маляр? Что можно

узнать, исходя из этих данных?

Аналогично ставятся вопросы, выясняется, сколько рам покрасит второй маляр за

один день, сколько покрасят рам оба маляра за один день, работая вместе, и

затем дается ответ на вопрос задачи. После этого составля­ется план,

записывается решение задачи. Другая задача предлагается для домашнего

решения.

Нельзя ли продумать и организовать деятельность учащихся при решении задачи

несколько иначе?

Да, возможен другой подход, основанный на сравнении задач и их решений, тем

более что содержание, структура задач и данные в их условии являются тем

благодатным материалом для использования приема срав­нения. Для этого можно

предложить детям прочитать задачи, сравнить их условия, вопросы. Выяснить,

чем похожи и чем отличаются задачи. Предложить подумать, можно ли, не решая

задачи, установить одинаковые или разные числа получатся в ответе. Пусть

учащиеся попробуют объ­яснить свои предположения. Если одинаковы, то почему?

Если разные, то в каком отношении будут находиться эти числа, в какой задаче

число в ответе будет больше и во сколько раз?

Устанавливая сходства и различия, на основе применения необоснованной

аналогии (чем больше объем выполненной работы, тем больше потребуется времени

для ее выполне­ния) большинство учащихся высказывают предположение (которое в

данном случае оказывается ошибочным), что в ответе второй задачи число будет

больше в 10 раз, чем в первой. В этом случае полезно провести беседу, в

процессе которой попытаться убедить детей, что такого быть не может. Вопросы,

предлагаемые детям, могут быть примерно такими:

— Сколько дней потребуется первому маляру, чтобы выполнить всю работу? (15

дней.)

— А второму? (10 дней.)

— Если оба маляра будут работать вместе, то больше или меньше потребуется им

времени для выполнения всей работы? (Ме­ньше, чем 10 дней.)

Аналогичные вопросы предлагаются и для второй задачи. Выясняется, что для

выполне­ния всей работы двум, мастерским потребу­ется меньше, чем 10 дней.

Таким образом, число в ответе второй задачи не может быть больше числа,

которое получается в ответе первой задачи.

В процессе анализа задач учащиеся нахо­дят решения и записывают их:

Задача 1

1) 150: 15= 10 — рам красил первый ма­ляр за один день.

2) 150:10=15—рам красил второй ма­ляр за один день.

3) 10+15=25 — рам красили оба маляра за один день.

4) 150: 25 =6 — за 6 дней выполнят всю работу оба маляра, работая вместе.

Задача 2

1) 1500:15= 100 — книг переплетает одна мастерская за один день.

2) 1500:10= 150 — книг переплетает дру­гая мастерская за один день.

3) 100+150=250 — книг переплетают обе мастерские за один день, работая вместе.

4) 1500:250= б — за 6 дней закончат работу обе мастерские, работая вместе.

Решение задачи дает возможность убе­диться, что предположение детей либо

под­твердилось, либо опровергалось.

Для более глубокого понимания сути рассматриваемого вопроса, решения задачи,

зависимости между величинами, входящими в задачу, полезно показать детям

графиче­ское решение. Для этого учитель заранее выполняет чертеж:

Пояснить построение чертежа можно при­мерно так: «Обозначим число рам длиной

данного отрезка. Эту работу маляр может выполнить за 15 дней. Значит, в день

он выполняет 1/5 часть (показывает на черте­же). Второй выполняет эту "

работу за 10 дней, в день он выполняет 1/10 часть (показать на чертеже). За

сколько дней выполнят эту работу оба маляра, работая вместе? Будем считать: I

— пятнадцатую часть, II — десятую (показывается на черте­же), во второй

день—пятнадцатую часть первый и десятую — второй и т. д. Дети считают число

дней и убеждаются, что и в первой и во второй задаче получится одинаковое

число дней, независимо от объ­ема выполненной работы.

Такая деятельность по решению задач будет в большей мере способствовать

форми­рованию творческой активности и мышления учащихся, возможности глубже

осмысливать взаимосвязи между величинами, входящими в задачу, формированию

осознанного поиска решения задач.

Высокую умственную активность проявля­ют учащиеся, выполняя анализ неверного

решения. Обратимся еще раз к рассмотрен­ной выше задаче.

Дело в том, что многие учащиеся, не вдумываясь в условие задачи, решают ее

следующим образом:

150: (15+10) =6.

Как поступить учителю в этом случае? Оставить без внимания неверное решение

или обсудить его со всеми учащимися? Некоторые идут по первому пути,

указывают ученику, что решение его неверно, и в процессе беседы подводят к

нужному правильному решению, т. е. показывают обра­зец рассуждений при

решении данной зада­чи. Таким образом, методика обучения решению задач

сводится к обучению по образцу.

Думается, что такой подход к обучению решению задач не всегда эффективен.

Учи­тель должен внимательно относиться к каж­дой из совершаемых проб поиска

пути решения задачи и в случае неудачи использо­вать ее с обучающей целью, с

целью активизации мыслительной деятельности учащихся, т. е. каждое неверное

решение должно быть проанализировано и установле­на причина ошибочного

решения. В данном случае можно поступить следующим обра­зом. Записать решение

на доске и, используя фронтальную беседу, доказать необоснован­ность данного

решения. Для этого нужно предложить детям проверить, правильно ли выбраны

действия. Обратить внимание на первое действие и, соотнеся его с условием

задачи, выяснить, что обозначает каждое число.

— Что обозначает число 15? (За 15 дней первый маляр может выполнить всю работу.)

— Что обозначает число 10? (За 10 дней второй маляр может выполнить всю работу.)

— Если оба маляра будут работать вместе, больше или меньше они затратят

времени, чтобы покрасить 150 рам? (Меньше; меньше, чем 10 дней.)

— Что же могло обозначать число 25, полученное в данном действии? (Число

дней, которое необходимо для покраски 300 рам, при условии, что первый маляр

красит 50 рам, затем начинает работать другой маляр, и заканчивают свою

работу за 10 дней.)

Полезно рассмотреть и второе действие. Выяснить, что при делении числа рам

(150) на число дней (25) в результате случается число рам (6), а в задаче

спрашивается о числе дней, за которое могут окрасить оба маляра 150 рам,

работая месте.

Такое обсуждение активизирует мыслительную деятельность учащихся,

вырабатывает привычку не начинать поиск решения задачи без глубокого, полного

анализа задачи, создает условия для эффективного формирования общего умения

решать задачи.

Задачи на пропорциональное деление.

Первой лучше включить задачу с величи­нами: ценой, количеством и стоимостью,

поскольку связи между ними усвоены уча­щимися лучше, чем связи между другими

величинами. Учитель предлагает составить задачу по ее краткой записи (запись

выпол­нена на доске):

Ученики составят примерно такую задачу:

«Два мальчика купили марки по одина­ковой цене. Первый купил 7 марок, а

вто­рой 5 марок. Марки первого мальчика стоили 35 к. Сколько стоили марки

второго мальчика?» Ученики устно решают эту за­дачу и узнают, что марки

второго мальчика стоили 25 к. Учитель записывает это число. В таблице вместо

вопросительного знака и предлагает найти сумму чисел, обозначаю­щих стоимость

марок. Выясняется, что 60 к. уплатили за марки оба мальчика. В краткую запись

вносятся изменения:

Ученики составляют задачу по этой крат­кой записи: «Два мальчика купили марки

по одинаковой цене. Первый купил 7 марок, второй — 5 марок. Всего они

уплатили 60 к. Сколько стоили марки первого мальчика? Сколько стоили марки

второго мальчика?» Учитель предлагает детям попытаться само­стоятельно решить

задачу, ответив на первый вопрос. С теми, кто затруднится это сде­лать,

проводит разбор, предлагая вопросы:

«Что требуется узнать в задаче? Можно ли сразу узнать, сколько стоили марки

первого мальчика? Почему нельзя? Можно ли сразу узнать, сколько марок купили на

60 к.? Почему можно? Что узнаете первым действи­ем? вторым? третьим?

четвертым?» Решение лучше записать отдельными действиями с по­яснениями. Для

проверки решения можно выполнить сложение чисел, полученных в от­вете, если их

сумма будет равна числу 60, то решение выполнено верно. Надо пояснить, что два

вопроса в таких задачах обычно заменяют одним вопросом со словом каждый,

например: «Сколько стоили марки каждого мальчика?» Важно подчеркнуть, что здесь

два вопроса и при решении будет два ответа.

Задачи на нахождение неизвестных по двум разностям.

Пусть надо ре­шить задачу: «В киоске продали по одинако­вой цене 12 синих

стержней для ручек и 8 черных. За синие стержни получили на 32 к. больше, чем

за черные. Сколько стоили синие стержни? Сколько стоили черные стер­жни?»

Выделив величины, данные в задаче, ученики записывают задачу кратко на доске

и в тетрадях:

Проводится беседа: «Почему за синие стержни уплатили больше денег, чем за

черные? (Синих стержней купили больше.) За сколько синих стержней уплатили

столь­ко же, сколько за все черные стержни? (За 8 стержней.) Сколько уплатили

за остальные синие стержни? (32 к.) Нельзя ли узнать, сколько стержней купили

на 32 к.? (Можно.) Составьте план решения. (Сна­чала узнаем, сколько стержней

стоили 32 к., выполнив вычитание; затем узнаем, сколько стоил 1 стержень,

выполнив деление; да­лее узнаем, сколько стоили синие стержни и сколько

стоили черные стержни действием умножения.)»

Задачи на встречное движение и движение в противоположных направлениях.

Например:

«Два велосипедиста выехали одно­временно навстречу друг другу из двух

поселков и встретились через 2 ч. Ско­рость одного из них 11 км/ч, а другого

13 км/ч. Найти расстояние между поселка­ми». После чтения задачи выполняется

под руководством учителя чертеж:

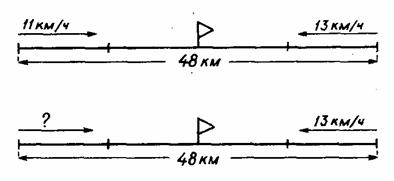
Выясняется, что каждый велосипедист был в пути до встречи 2 ч, что первый

пройдет до встречи меньшее расстояние, так как он двигался с меньшей

скоростью, и что расстоя­ние между поселками складывается из расстояний,

пройденных каждым из велосипедистов до встречи. После этого, как пра­вило,

ученики сами составляют план реше­ния: узнаем расстояние, пройденное пер­вым

велосипедистом до встречи, выполнив умножение; затем узнаем расстояние,

прой­денное вторым велосипедистом до встречи, выполнив умножение; после чего

найдем рас­стояние между поселками, сложив оба рас­стояния. Решение лучше

записать отдель­ными действиями с пояснениями.

Для разбора решения этой задачи другим способом можно проиллюстрировать

движе­ние, вызвав к чертежу двух учеников. Учи­тель ведет объяснение: «Вы

будете велоси­педистами. Покажите указкой, откуда вы на­чали движение. Вы

начали двигаться одно­временно и ехали 1 ч. Сколько километ­ров проехал за

это время каждый из вас? (11 км и 13 км.) Подпишем 11 км и 13 км на чертеже.

На сколько километров вы сблизились за 1 ч? (На 24 км.) прошел еще 1 ч. На

сколько километров вы еще сбли­зились? (На 24 км.) Встретились ли

вело­сипедисты? (Да.) Составьте план решения. (Сначала узнаем, на сколько

километров сближались велосипедисты в час, выпол­нив сложение; затем найдем

расстояние меж­ду поселками, выполнив умножение.)» Эти два способа решения

надо сравнить и. оце­нить, какой из них рациональнее.

Задачи, обратные данной, ученики могут составить сами по преобразованным

чер­тежам, которые выполняет учитель. Снача­ла искомым становится время

движения до встречи, а затем

скорость одного из вело­сипедистов. Вот эти измененные чертежи:

План решения той и другой задачи уче­ники могут составить сами. Решение лучше

записать отдельными действиями. Затрудне­ние обычно вызывает один из способов

решения последней задачи (48:2=24, 24-13= 11). В этом случае, обращаясь к

иллю­страции, надо показать, что в каждый час велосипедисты сближались на

одинаковое расстояние, поэтому легко узнать, на сколько километров они

сближались в час, выпол­нив деление (48:2=24), зная это и скорость одного из

них, можно найти скорость дру­гого (24—13=11).

Теперь полезно сравнить задачи, выявив сходное (все задачи на встречное

движе­ние, в них одинаковые величины) и раз­личное (в первой задаче находили

расстояние по известным скорости каждого велосипеди­ста и времени движения до

встречи; во второй задаче находили время движения до встречи по известным

расстоянию и скорости каждого велосипедиста; в третьей задаче находили

скорость одного из велосипедистов по известным расстоянию, времени движения

до встречи и скорости другого велосипеди­ста). Сравнив решения, ученики

должны за­метить, что каждую задачу можно решить двумя действиями, причем в

этом случае первым действием находили, на сколько ки­лометров сближались

велосипедисты в час, но при решении первой и второй задачи это находили

сложением, а при решении третьей задачи — делением. Далее, как и в других

случаях, на последующих уроках ученики решают задачи этих видов сначала под

руководством учителя, а затем самостоятельно. Здесь так же, как и при решении

других задач, полезно предлагать различные упражнения творческого характера.

В част­ности, ставить вопросы вида: «Могли ли ве­лосипедисты (теплоходы и т.

п.) встретиться на середине пути? При каких условиях? Если велосипедисты

после встречи продол­жат движение, то какой из них приедет раньше к месту

выхода другого велоси­педиста, если будет двигаться с той же скоростью?»

Рассмотрим задачу, решающуюся несколькими способами:

«В зале 8 рядов стульев, по 12 стульев в каждом ряду. В зал пришли ученики из

двух классов, по 42 ученика в каждом. Хватит ли стульев для учеников? Если

останутся незанятые, то сколько?»

Используя разбор задачи от данных к во­просу, дети легко получили решение,

рассуж­дая следующим образом: «Зная, что в зале 8 рядов по 12 стульев в каждом

ряду, найдем, сколько всего стульев в зале: 12×8=96. Те­перь определим,

сколько стульев будет заня­то, т. е. узнаем, сколько учеников в двух классах.

Столько же будет занято и стульев: 42×2= 84. Сравним теперь число всех

стульев - 96 и число стульев, которые займут ученики двух классов, - 84.

96>84, значит, стульев хватит. 96—84=12. 12 стульев останутся незанятыми».

Чтобы отыскать другие способы решения, я предложила детям представить, как

могли ученики двух классов войти в зал и в соответ­ствии с этим дополнить

условие задачи. Рассуждая, сопоставляя, дети отыскали три способа решения. И

эти три способа записали в тетрадь:

II способ

1) 2.8=96

2) 96-42=54

3) 54—42=12

О т в е т. 12 стульев останутся незанятыми.

Вначале свои места заняли ученики одного класса, а затем другого.

III способ

Всех учащихся рассадили так, чтобы все места в ряду были заняты, т. е. в

каждом ряду было по 12 человек:

1) 42×2=84 — места займут ученики двух классов;

2) 84:12= 7 — рядов займут ученики двух классов;

3) 8-7= 1 — ряд или 12 стульев останутся незанятыми.

Ответ: 12 стульев останутся незанятыми.

IV способ

Стулья в зале распределили поровну между классами, т. е. по 48. Поэтому

сначала узнаем, сколько незанятых стульев осталось у каждо­го класса.

1) 12×8== 96 — всего стульев в зале;

2) 96:2=48—стульев для каждого класса;

3) 48-42== 6 — незанятых стульев у каж­дого класса;

4) 6•2== 12 — всего незанятых стульев. Ответ: 12 стульев останутся незанятыми.

Дети были удивлены, что задача имеет столько способов решения, и довольны,

что нашли их. Но когда я сказала, что эта задача имеет еще столько же и даже

больше решений, удивлению не было границ. Ребятам захотелось тут же отыскать

их, но поскольку урок подходил к концу, они попросили остаться после уроков,

чтобы в тот же день попытаться выявить все способы.

На этом дополнительном занятии опира­лась на способных ребят, вовлекала их в

самостоятельный поиск, предлагая им представить, как еще можно рассадить

учеников: чтобы все ряды заполнялись учени­ками равномерно и каждый ряд был

хотя бы частично занят; чтобы все места в рядах были заняты; чтобы оба класса

рассаживались одновременно; рассаживались порознь; чтобы для каждого класса

выделялось поровну мест в зале или поровну (по 6) в каждом ряду

Чтобы дети лучше могли представить все ситуации, на доске нарисовали 8 рядов,

по 12 кружков в каждом ряду.

Вот какие решения мы нашли, причем некоторые способы отыскали сами дети.

V способ

1) 42:12=3 (ост. 6)—3 ряда занято, оставшихся 6 учеников посадили в 4-й ряд;

2) 12-6= 6 —учеников из другого класса тоже посадили в 4-й ряд;

3) 42-6= 36 — учеников остается поса­дить на другие ряды;

4) 36:12=3 —еще 3 ряда займут ученики другого класса;

5) 4+3= 7—рядов занято;

6) 8-7 = 1 — ряд или 12 стульев не заняты.

Ответ: 12 стульев останутся незанятыми.

VI способ

1) 42:12=3 (ост. 6)—3 ряда занято, 6 учеников не посажено;

2) 42+6== 48—учеников осталось поса­дить;

3) 48:12== 4—ряда займут оставшиеся ученики;

4) 4+3== 7—рядов занято;

5) 8-7= 1 — ряд или 12 стульев не занято.

VII способ

1) 8:2== 4 — ряда для каждого класса;

2) 12 • 4= 48 — стульев выделили для каж­дого класса;

3) 48-42== 6—стульев остается незаня­тыми в каждой части зала, выделенной

каждому классу;

4) 6-2== 12—стульев останутся незаня­тыми.

VIII способ

1) 42×2= 84—ученика нужно посадить;;

2) 84:8== 10 (ост. 4) — 10 учеников в каж­дом ряду и 4 учеников пока не

посадили, если будем сажать поровну на каждый ряд;

3) 12-10== 2 — по 2 стула осталось неза­нятыми в каждом ряду;

4) 2-8== 16—всего 16 стульев осталось после того, как рассадили по 10

учеников в каждом ряду;

5) 16-4== 12 — стульев остались незаня­тыми, после того как 4 оставшихся

учеников посадили на места из оставшихся 16;

IX способ

1) 12-8== 96—всего стульев в зале;

2) 96:42=2 (ост. 12)—2 класса можно посадить и 12 мест останутся незанятыми.

Х способ

1) 12:2=6 — по 6 стульев в ряду выделили для класса, если будем рассаживать

на каждый ряд поровну учеников из одного и другого класса;

2) 42:6== 7 — рядов займет каждый класс;

3) 8—7== 1 — ряд или 12 стульев останутся незанятыми

Дети просто были потрясены таким обили­ем способов. И поскольку ситуация

задачи несложна для представления (тем более что на рисунке на доске

показывали, как они «рассаживают» учеников), записывали мы только некоторые

способы с самой короткой записью. Остальные выполняли устно с пока­зом на

рисунке, определяли самый рациональ­ный способ.

Потом оказалось, что эта задача имеет еще по крайней мере, четыре способа

решения. Приведем один из них.

XI способ

1) 42-2 ==84—ученика в двух классах и 84 стула нужно для всех;

2) 96:84= 1 (ост. 12) — 1 раз по 84 стула содержится в зале и 12 стульев

останутся незанятыми.

Работа по отысканию разных способов решения задач так заинтересовала детей,

что если даже на уроке не планировалось решение задач несколькими способами,

учащиеся самостоятельно находили их. Всегда были дети, которые стремились

решить задачу нетрадиционным способом.

Рассмотрим несколько задач, решаемых по системе Л.В.Занкова арифметическим и

алгебраическим способом:

Задача №1

"Из 560 листов бумаги сделали 60 тетрадей двух сортов. На каждую тетрадь

первого сорта расходовали по 8 листов, а на каждую тетрадь второго сорта - по

12 листов. Сколько сделали тетрадей каждого сорта?" К задаче даны два

указания:

1. Решить задачу алгебраическим способом.

2. Предложить свое задание к задаче.

Следуя указанию учебника, учитель подво­дит учащихся к составлению уравнения,

рас­суждая примерно так: "Обозначим буквой х - число тетрадей первого сорта,

тогда тетрадей второго сорта будет (60 - х). Известно, что на те­традь

первого сорта расходовали 8 листов, зна­чит, (8х) листов расходовали на

тетради первого сорта. На тетрадь второго сорта расходовали 12 листов.

Следовательно, на тетради второго сор­та израсходовано 12 (60-х) листов.

Теперь мож­но найти, сколько всего листов израсходовано:

(8х + 12 (60-х), а это по условию равно 560. Со­ставим уравнение: 8х + 12 (60

- х) = 560. Ис­пользуя дистрибутивный закон (правило умно­жения числа на

разность), дети записывают уравнение: 8х + 720 - 12х = 560.

И если составление уравнения не вызывает затруднений у учащихся, то при его

решении возникают определенные трудности.

Действительно, действия с отрицательны­ми числами будут изучаться позднее, а

реше­ние требует выполнения операций над ними.

Приведем образец решения уравнений.

8х+ 12 (60-х) =560

8х+720-12х=560

8х + 720 - 720 - 12х = 560 - 720 (из обеих частей уравнения вычли по 720)

8х- 12х =-160

(8 - 12)х = - 160 (применили дистрибутив­ный закон умножения относительно

вычита­ния, вынесли неизвестное число х за скобки)

-4х=-160

х=(-160):(-4)

х=40

Итак, чтобы найти неизвестное число, нуж­но обе части уравнения разделить на

(- 4), т.е. необходимо провести операции с отрицательны­ми числами, а понятие

об отрицательном числе будет изучаться позднее.

Чтобы избежать этого, учитель может по­пытаться решить это уравнение

следующим образом:

8х+ 12(60-х)=560

8х+720- 12х =560

8х+720+12х-12х=560+12х прибавим 12х

8х+720=560+ 12х

8х - 8х + 720 = 560 + 12х - 8х вычитаем из обеих частей 8х

720 = 560 + (12 - 8)х выносим за скобки х

720 - 560 = 560 - 560 + 4х вычитаем из обе­их частей 560

160=4х

х= 160:4

х=40

Согласитесь, что подобные рассуждения слишком громоздки и затруднительны.

Зная это, учитель подводит учащихся к другому уравне­нию, решение которого

легче и понятнее детям. Рассуждения примерно таковы: "Пусть х - число

тетрадей второго сорта. Тогда (60-х) - число те­традей первого сорта. На

тетради второго сорта пошло 12х листов, а на тетради первого -8 (60 - х)

листов. На все тетради пошло 12х + 8 (60 - х) листов бумаги. По условию

зада­чи это равно 560 листам". Составляем уравнение:

12х+8 (60-х) =560

12х+480-8х=560

12х-8х =560-480

(12-8)х=80

4х=80

х = 80 : 4

х=20

Ответ: 20 тетрадей второго сорта, 40 тет­радей первого сорта (60 - 20 = 40).

Рассуждения учителя и учащихся могут быть примерно такими: "Предположим, что

все тетради были тетрадями первого сорта. Тог­да потребовалось бы 8 • 60 =

480 листов бумаги. Но в условии задачи сказано, что пошло 560 ли­стов, т.е.

израсходовано больше, чем предполо­жили, на 80 листов (560 - 480 = 80) за

счет того, что были тетради другого сорта, на которые шло по 12 листов. На

одну тетрадь второго сорта рас­ходовали больше на 4 листа. Итак, на все

тетра­ди второго сорта израсходовали на 80 листов больше, а на каждую тетрадь

- на 4 листа боль­ше. Это значит, тетрадей второго сорта будет столько,

сколько раз укладывается 4 в числе 80: 80:4 = 20 (тетрадей). Чтобы найти

число те­традей первого сорта, нужно из 60 вычесть 20". Затем записывается

решение задачи:

1)80-60=480

2) 560 - 480 = 80

3) 12-8=4

4) 80 : 4 = 20

5) 60 - 20 = 40

Второй арифметический способ решения основан на предположении, что все

тетради были второго сорта.

Аналогичные рассуждения приводят к ре­шению:

1) 12 • 60 = 720 тетрадей

2) 720 - 560 = 160 тетрадей

3) 12-8 =4 тетради

4) 160 : 4 = 40 тетрадей

5) 60 - 40 = 20 тетрадей \

Ответ: 40 тетрадей первого сорта, 20 тет­радей второго сорта.

Возможны и другие способы решения за­дачи. Например:

1) 12.60=720

2)720-560= 160

3)12-8=4

4) 160:4=40

5) 8 • 40 = 320

6)560 - 320 = 240

7)240: 12=20

Задача №2

«На запасных путях стояло 2 железнодорожных состава. В первом составе было на

12 вагонов больше, чем во втором. Когда от каждого состава отцепили по 6

ва­гонов, в первом оказалось в 4 раза больше ваго­нов, чем во втором. Сколько

вагонов было в каждом составе?»

К данной задаче даны три указания: 1) ре­шить задачу алгебраически; 2) найти

среди ре­шенных раньше задач похожую на данную ре­шением; 3) составь свою

задачу, которая будет иметь такое же решение.

При решении задачи алгебраическим спо­собом учащиеся обозначают буквой х -

число вагонов в первом составе, тогда во втором со­ставе число вагонов (х -

12). В задаче сказано, что от каждого состава отцепили по 6 вагонов. Во

втором составе ока­залось (х - 18) вагонов, а в первом (х - 6) ваго­нов. В

первом составе в 4 раза больше вагонов, чем во втором.

Составим уравнение: х - 6 = 4 (х - 18). При решении уравнения у учащихся

появляются затруднения, связанные с тем, что возникает необходимость в

выполнении дейст­вий с отрицательными числами:

х - 6 = 4х- - 72

х - 4х = - 72 + 6

- 3х = - 66

х = (- 66): (- 3)

х=22

Чтобы избежать таких недоразумений, учитель предлагает на основе изученных

свойств числовых равенств (вернее, равно­сильности уравнений) неизвестное

перенести в правую часть уравнения:

х- 6=4 (х- 18)

х - 6 = 4х - 72

- 6 = 4х - х - 72

-6 =(4-1) х-72

- 6 = Зх - 72

- 6 + 72 = Зх

72 - 6 = Зх

66=3х

х=22

Как видим, решение уравнения вызывает затруднения у учащихся, и, предвидя

это, учи­тель в процессе рассуждения подводит детей к уравнению, решение

которого проще:

4 (х- 18)= х-6

4х - 72 = х - 6

4х-х-72=х-х-6

(4- 1) х-72 =-6

Зх = 72 - 6

х = 66 : 3

х = 22 (вагона в первом составе)

Ответ: в первом составе - 22 вагона, во втором - 10.

Обозначив буквой х число вагонов второго состава, в процессе рассуждении

можно полу­чить уравнение:

4 (х - 6) = х + 6

4х - 24 = х + 6

Зх = 6 + 24

Зх=30

х= 10

Таким образом, можно с уверенностью ска­зать, что при решении задач

алгебраическим способом учителю необходимо продумать, ка­кое неизвестное

обозначить буквой, и подвес­ти учащихся к уравнению, решение которого будет

проще и понятнее для них.

Выполнение второго задания, предложен­ное автором, для данной задачи сводится

к отысканию (узнаванию) среди решенных по­хожей задачи, что отнимает много

времени и недостаточно эффективно с точки зрения раз­вития умственных

способностей.

Третье задание (составить задачу, похожую на данную) преследует такую же

цель, как и второе.

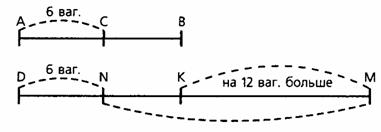
Думается, в данном случае целесообразно решить задачу арифметическим

способом. Для осознанного поиска решения задачи необходи­мо проиллюстрировать

задачную ситуацию с помощью чертежа. Например, изобразить чис­ло вагонов

второго состава отрезком АВ. От состава отцепили 6 вагонов (показываем на

чертеже). Оставшееся число вагонов будет со­ответствовать отрезку СВ.

В задаче сказано, что вагонов осталось в пер­вом составе в 4 раза больше, чем

во втором. Зна­чит, числу оставшихся вагонов первого состава будет

соответствовать отрезок в 4 раза больше, чем отрезок СВ (показываем на

чертеже отрезок ММ). Первоначально в первом составе было на 6 вагонов больше

(показываем на чертеже). DN -отрезок, соответствующий 6 вагонам, тогда ОМ

соответствует числу вагонов первого состава).

Рассматривая чертеж, необходимо обра­тить внимание детей на то, что отрезку

КМ со­ответствует 12 вагонов. В задаче сказано "на 12 вагонов больше", и эти

12 вагонов прихо­дятся на три равные части, каждая из которых равна отрезку

СВ (числу вагонов, оставшихся во втором составе).

После такой наглядной интерпретации за­дачи дети самостоятельно записывают

реше­ние и поясняют каждое выполняемое действие:

1)4-1=3 (на 3 части больше осталось ва­гонов в первом составе)

2) 12 : 3 = 4 (вагона осталось во втором составе)

3) 4 + 6 = 10 (вагонов было во втором составе)

4) 10 + 12 = 22 (вагона было в первом составе)

При сравнении способов решения учащие­ся приходят к выводу, что

арифметический способ легче и понятнее, чем алгебраический.

Интересным для учащихся будет и реше­ние данной задачи методом перебора.

Прежде всего определим, с какого числа можно (да и нужно) начинать подбор

чисел. В задаче сказано, что от каждого состава отцепи­ли по 6 вагонов и при

этом вагоны еще оста­лись. Значит, вагонов в составе было больше шести. В

задаче также сказано, что в первом составе осталось вагонов в 4 раза больше,

чем во втором. Значит, осталось четное число ваго­нов (любое число,

умноженное на четное, есть число четное). Если отцепили 6 вагонов (а 6 -число

четное), значит, вначале было тоже чет­ное число вагонов (сумма двух четных

чисел есть число четное). Во втором составе на 12 вагонов меньше, а это

значит, что и во втором составе четное число вагонов. Итак, для пробы будем

брать следующие числа: 8, 10, 12 и т.д.

Пусть во втором составе было 8 вагонов, тог­да в первом их было 20 (8 + 12 =

20). Когда от каждого состава отцепили по 6 вагонов, в первом оказалось

14(20-6=14), а во втором-2 (8 - 6 = 2). Проверяем, во сколько раз 14 боль­ше,

чем 2(14:2=7)-в7 раз. Это не соответст­вует условию задачи, так как число

оставшихся вагонов первого состава должно быть в 4 раза больше, чем число

вагонов второго состава. Пусть 10 число вагонов второго состава. Тогда число

вагонов первого состава 22 (10 + 12 = 22).

От каждого отцепили по 6 вагонов: во втором ос­талось 4, в первом - 16 (10 -

6 = 4, 22 - 6 = 16). Проверяем, во сколько раз больше осталось ваго­нов в

первом составе, чем во втором, и получаем 4(16:4=4), что соответствует

условию задачи.

Ответ: в первом составе было 22 вагона, во вто­ром — 10.

Заключение.

Решение текстовых задач и нахождение разных способов их решения на уроках

математики способствуют развитию у детей мышления, памяти, внимания,

творческого воображения, наблюдательности, последовательности рассуждения и

его доказательности; для развития умения кратко, четко и правильно излагать

свои мысли.

Решение задач разными способами, получение из нее новых, более сложных задач

и их решение в сравнении с решением исходной задачи создает предпосылки для

формирования у ученика умения находить свой «оригинальный» способ решения

задачи, воспитывает стремление вести «самостоятельно поиск решения новой

задачи», той, которая раньше ему не встречалась.

Задачи с многоспособовыми решениями весьма полезны так же для внеклассных

занятий, так как при этом открываются возможности по настоящему

дифференцировать результаты каждого участника.

Такие задачи могут с успехом использоваться в качестве дополнительных

индивидуальных знаний для тех учеников, которые легко и быстро справляются с

задачей на уроке, или для желающих в качестве дополнительных домашний

заданий.

Список используемой литературы.

1. Бантова М.А. Решение текстовых арифметических задач. Журнал «Начальная

школа» №10-11 1989г. МОСКВА. “Просвещение”.

2. Баринова О.В. Дифференцированное обучение решению математических

задач. Журнал «Начальная школа» №2 1999г. МОСКВА. “Просвещение”.

3. Вялова С. Как составить и решить задачу. Газета «Начальная школа» №16,

№19 1998г. МОСКВА.

4. Гребенникова Н.А. Ознакомление первоклассников с задачей. . Журнал

«Начальная школа» №10 1990г. МОСКВА. “Просвещение”.

5. Гребенникова Н.Л. Решение задач на зависимость величин разными

способами. Журнал «Начальная школа» №2 1999г. МОСКВА. “Просвещение”.

6. Захарова Н.М. Простые задачи в системе УДЕ. Журнал «Начальная школа»

№3 1997г. МОСКВА. “Просвещение”.

7. Клименченко Д. Задачи с многовариантными решениями. Журнал «Начальная

школа» №6 1991г. МОСКВА. “Просвещение”.

8. Мельник Н.В. Развитие логического мышления при изучении математики.

Журнал «Начальная школа» №5 1997г. МОСКВА. “Просвещение”.

9. Мельникова Т.С. Таблицы по математике. Журнал «Начальная школа» №1

1990г. МОСКВА. “Просвещение”.

10. Моро М.И. Методические указания к демонстрационному

материалу по математике. МОСКВА. “Просвещение”. №2 1999г.

11. Семья Ф. Совершенствование работы над составными задачами.

Журнал «Начальная школа» №5 1991г. МОСКВА. “Просвещение”.

12. Солнышко Г.М. Как научить ребенка самостоятельно решать

задачи. Газета «Начальная школа» №21 1998г. МОСКВА.

13. Стойлова Л.П. Основы начального курса математики. №2 1999г.

МОСКВА. “Просвещение”.

14. Целищева И.И. Моделирование в процессе решения текстовых

задач. Журнал «Начальная школа» №3 1996г. МОСКВА. “Просвещение”.

15. Шадрина И.В. Использование графических схем при работе над

текстовой задачей. Журнал «Начальная школа» №3 1995г. МОСКВА. “Просвещение”.

16. Шикова Р.Н. Работа над текстовыми задачами. Журнал

«Начальная школа» №5 1991г. МОСКВА. “Просвещение”.

17. Шикова Р.Н. Особенности работы над задачами по системе

развивающего обучения Л.В. Занкова. Журнал «Начальная школа» №4 1999г.

МОСКВА. “Просвещение”.

18. Шульга Р.П. Решение текстовых задач разными способами –

средство повышения интереса к математике. Журнал «Начальная школа» №12 1990г.

МОСКВА. “Просвещение”.

Приложение 1.

Памятка

В задаче дано (говорится, что.).

Спрашивается.

Рассуждаю (ребенок может выбрать способ рассуждения сам):

а) от данных к искомой величине (перфокарта 1);

б) от искомого к данным (перфокарта 2);

Решаю.

Проверяю.

Приложение 2.

Перфокарта №1

1. Зная, что красных шаров 7, а синих – на 3 больше.

2. Я могу узнать: синие шары – 7+3.

3. А чтобы узнать количество синих и красных шаров вместе, надо к красным

шарам (7 штук) прибавить синие (10 штук). 7+10=17

4. Проверяю: 17-7=10, 10-7=3

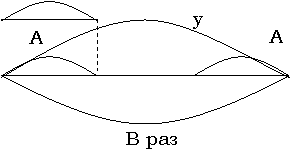
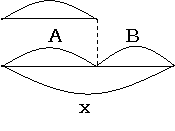
Перфокарта №2

1. Для ответа на вопрос надо знать:

а) количество красных шаров.

б) количество синих шаров.

2. В задаче известно: красных шаров – 7 штук.

Неизвестно: количество красных шаров.

Но сказано, что их на 3 штуки больше (7+3).

3. Значит, сначала узнаю количество синих шаров:

7+3=10 шт.

Затем узнаю количество красных и синих шаров вместе: 7+10=17 шт.

4. Проверяю: 17-7=10, 10-7=3

Приложение 3.

Схемы-формулы, используемые при решении задач по системе Д.Б. Эльконина –

В.В. Давыдова.

Больше на . больше в . раз

х=А+В у=АхВ

		х
						К раз

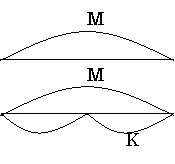
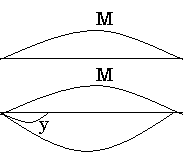
меньше на . меньше в . раз

х=М-К у=М:К

Приложение 4.

Виды кратких записей задач.

Карточка №1. Задачи на нахождение суммы.

Карточка №2. Задачи на увеличение или уменьшение числа на несколько единиц.

Карточка №3. Задачи на нахождение остатка.

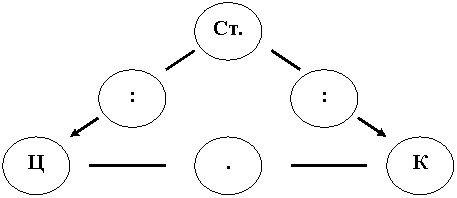
Приложение 5.

При решении задач на цену, количество и стоимость можно использовать данную

схему:

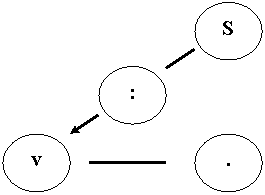
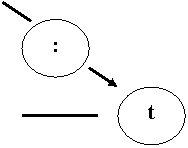
При решении задач на движение можно использовать следующую схему (запомним,

что латинской буквой “S” обозначается расстояние, буквой “t” – время, буквой

“v” – скорость):

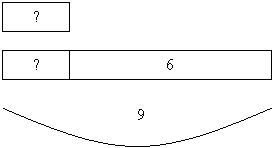
Приложение 6.

1. На каждой из двух полок было по 3 книги. Когда несколько книг добавили на

вторую полку, то на ней стало 9 книг. Сколько книг добавили на вторую полку?

2. На первой полке было 3 книги, на второй – 9 книг. Во сколько раз уменьшили

число книг на второй полке, если их стало столько же, сколько и на первой?

3. На двух полках книг было поровну. Когда число книг на второй полке

увеличили в 3 раза, то их на второй полке стало 9, сколько книг сначала было

на каждой полке?

4. На двух полках книг было поровну. Когда на вторую полку поставили еще 6

книг, то на второй полке стало 9 книг. Сколько книг было сначала на каждой

полке?

5. На первой полке было 3 книги, на второй полке – 9 книг. Когда взяли

несколько книг со второй полки, то их стало столько же, сколько на первой.

Сколько книг взяли на второй полке?

Ниже приведены рисунки к задачам. Сопоставьте каждой задаче соответствующий

рисунок.

Рис. 1.

Рис. 2.

Рис. 3.

Рис. 4.

Рис. 5.

Во сколько раз уменьшили.?

Приложение 7.

Порядок работы с задачей.

УСЛОВИЕ

ЗАДАЧА РЕШЕНИЕ ПРОВЕРКА ОТВЕТ

Приложение 8.

Задача №1:

Рабочему поручено изготовить 30 деталей за 10 ч. Но рабочий, экономя время,

успевал делать одну деталь за 15 мин. Сколько деталей сверх задания сделал

рабочий за счет сэкономленного времени? (При решении 10 ч заменить минутами.)

Дополнительные задания:

1. Найдите два способа решения задачи.

2. Объясните, как рассуждал ученик, который решил эту задачу таким способом:

I способ

10 ч = 600 мин

1) 600:15=40 – деталей

2) 40-30=10 – деталей

II способ

1) 600:30=20 – минут

2) 20-15=5 – минут

3) 5·30=150 – минут

4) 150:15=10 – деталей

3. Решите эту задачу другими способами, отвечая на поставленные вопросы:

III способ

1) Сколько деталей стал делать рабочий за 1 ч?

2) Сколько деталей сделал рабочий за 10 ч?

3) Сколько деталей сделал рабочий сверх задания?

IV способ

1) Сколько минут должен был тратить рабочий на изготовление одной

детали?

2) Сколько деталей сделал рабочий за 1 ч сначала?

3) Сколько деталей он стал делать потом?

4) На сколько больше деталей стал делать рабочий за 1 ч?

5) Сколько деталей сделал рабочий сверх задания?

4. Так как эта задача допускает еще и другой способ решения:

1) 15·30=450 – минут затратил рабочий на изготовление 30 деталей, расходуя

на каждую по 15 мин.

2) 600-450=150 – минут осталось у рабочего на изготовление дополнительных

деталей.

3) 150:15=10 – деталей сделал рабочий сверх задания, то можно предложить

детям найти этот способ решения задачи.

Задачи, воспитывающие гибкость мышления, когда по одному действию требуется

восстановить весь дальнейший ход рассуждения.

Задача №2:

Нужно привезти 540 т угля на трех машинах. За сколько дней это можно сделать,

если на каждую грузить по 3 т и делать по 5 поездок в день?

Дополнительные задания:

1. Эту задачу можно решить разными способами. Закончите решение задачи

другими способами:

I способ

1) 3·5=15 – тонн перевезет одна машина в день.

2) .

3) .

II способ

1) 3·3=9 – перевезут три машины за одну перевозку.

2) .

III способ

1) 540:3=180 – тонн нужно перевезти каждой машине.

2) .

3) .

2. Найдите еще другие способы решения этой задачи (их не менее 12).

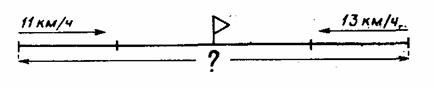
Страницы: 1, 2, 3