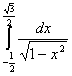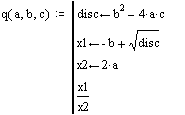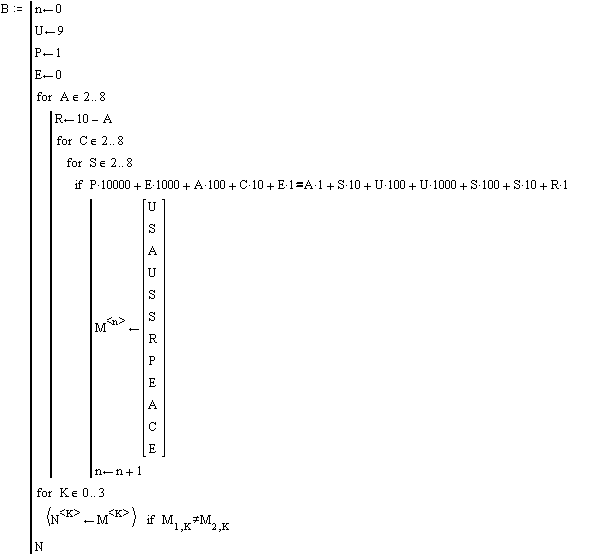Реферат: Обучение информатике
4. 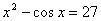 9. 9. 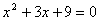
5. 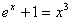 10. 10. 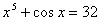
Задание 2. Решить систему уравнений.
1. 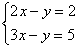 5. 5. 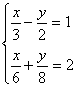 9. 9. 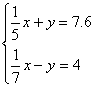
2. 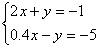 6. 6. 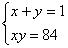 10. 10. 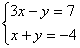
3. 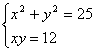 7. 7. 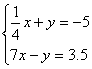
4. 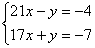 8. 8. 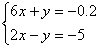
ЛАБОРАТОРНАЯ РАБОТА №3.
Тема. Дифференцирование функции. Геометрический смысл производной.
Цель. Научиться находить численное значение производной функции в
заданной точке.
Краткие сведения.
I. Вычисление производной функции.
Оператор производной Mathcad предназначен для нахождения численного значения
производной функции в заданной точке. Для вычисления производной используется
клавиша со знаком ?.
Для того, чтобы найти производную функции и вычислить ее численное значение,
необходимо сделать следующее:
Ø Сначала определить точку, в которой необходимо найти производную.
Ø Щелкнуть ниже определения этой точки. Затем набрать ?. Появится
оператор производной с двумя полями: 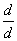
Ø Щелкнуть на поле в знаменателе и набрать имя переменной, по
которой проводится дифференцирование.
Ø Щелкнуть на поле справа от 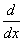
и набрать выражение, которое нужно дифференцировать.
Ø Чтобы увидеть результат, нажать знак =.
ПРИМЕР 1. Найти производную 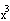 по по 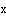 в точке в точке 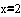 
Решение:
Определим точку, в которой необходимо найти производную:

Введем оператор производной, заполним поля и вычислим производную:
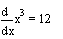
Помните!
Ø Результат дифференцирования есть не функция, а число – значение
производной в указанной точке переменной дифференцирования.
Хотя дифференцирование возвращает только одно число, можно определить одну
функцию как производную другой функции. Например: 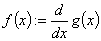
.
Вычисление f(x) будет возвращать в численной форме производную g(x) в точке х.
Выражение, которое нужно дифференцировать, может быть вещественным или
комплексным.
Переменная дифференцирования должна быть простой неиндексированной переменной.
II. Геометрический смысл производной.
ПРИМЕР 2
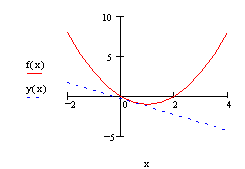
Дана функция у=f(x). Построить график функции и касательную к графику в точке с
абсциссой x=x0 , если 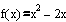 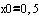 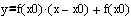
- уравнение касательной.
Решение:
Введем данную функцию и найдем ее значение в точке 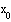 : :
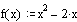
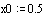
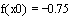
Найдем значение производной данной функции в точке 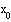 : :
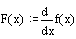
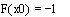
Запишем уравнение касательной для данной функции:
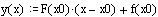
Построим график данной функции и касательную к ней.
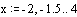
Задания для самостоятельного выполнения.
Задание 1. Найти производную функции в произвольной точке.
1. 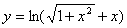 5. 5. 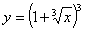 9. 9. 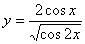
2. 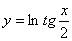 6. 6. 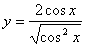 10. 10. 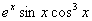
3. 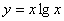 7. 7. 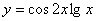
4. 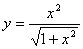 8. 8. 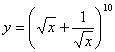
Задание 2.
Дана функция y=f(x). Построить график функции и касательную к графику в точке
с абсциссой x=x0. Y=f(x0)(x-x0)+f(x0) – уравнение касательной.
1. 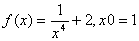 6. 6. 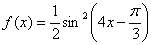 , x0=π∕6 , x0=π∕6
2. 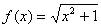 , x0=2 7. , x0=2 7. 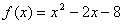 , x0=-1 , x0=-1
3. 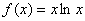 , x0=e 8. , x0=e 8. 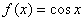 , x0=-π/2 , x0=-π/2
4. 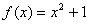 , x0=-1 9. , x0=-1 9. 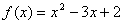 , x0=3 , x0=3
5. 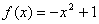 , x0=1 10. , x0=1 10. 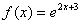 , x0=-2 , x0=-2
ЛАБОРАТОРНАЯ РАБОТА №4.
Тема. Интегральное исчисление.
Цель. Научиться находить определенные интегралы функций,
вычислять площадь фигуры при помощи интеграла.
Краткие сведения.
I. Определенный интеграл.
Оператор интегрирования в Mathcad предназначен для численного вычисления
определенного интеграла функции по некоторому интервалу.
Знак интеграла выводится при нажатии клавиши со знаком &.
Для того, чтобы вычислить определенный интеграл, необходимо сделать следующее:
Ø Щелкнуть в свободном месте и набрать знак &. Появится знак
интеграла с пустыми полями для подынтегрального выражения, пределов
интегрирования и переменной интегрирования: ∫
Ø Щелкнуть на поле внизу и набрать нижний предел интегрирования.
Щелкнуть на верхнем поле и набрать верхний предел интегрирования.
Ø Щелкнуть на поле между знаком интеграла и d и набрать выражение,
которое нужно интегрировать.
Ø Щелкнуть на последнее пустое поле и набрать переменную
интегрирования.
Ø Чтобы увидеть результат, нажать знак =.
ПРИМЕР 1 Вычислить определенный интеграл 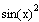 от 0 до p/4. от 0 до p/4.
Решение:
Введем знак интеграла и заполним пустые поля;
вычислим интеграл:
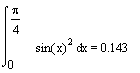
Помните!
Ø Пределы интегрирования должны быть вещественными. Выражение,
которое нужно интегрировать может быть вещественным, либо комплексным.
Ø Кроме переменной интегрирования, все переменные в
подынтегральном выражении должны быть определены ранее в другом месте
рабочего документа.
Ø Переменная интегрирования должна быть простой переменной без
индекса.
Ø Если переменная интегрирования является размерной величиной,
верхний и нижний пределы интегрирования должны иметь ту же самую размерность.
II. Площадь фигуры.
Как известно, при помощи определенного интеграла можно вычислять площадь фигуры.
ПРИМЕР 2. Найти площадь фигуры, ограниченной графиками функций:
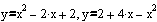
Решение.
Построим графики этих функций в одном графическом блоке:
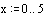
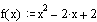
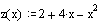
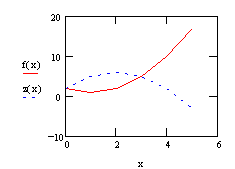
Вычислим площадь полученной фигуры:
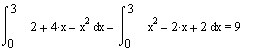 (кв.ед.) (кв.ед.)
Задания для самостоятельного выполнения.
Задание 1. Вычислить определенный интеграл.
1. 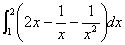 5. 5.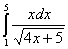 9. 9.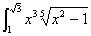 dx dx
2. 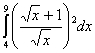 6. 6. 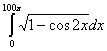 10. 10.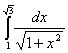
3. 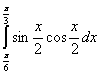 7. 7. 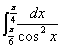
4. 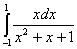 8. 8. 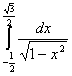
Задание 2. Найти площадь фигуры, ограниченной графиками функций.
Построить эту фигуру.
1. 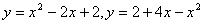 6. 6. 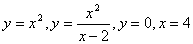
2. 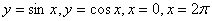 7. 7. 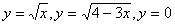
3. 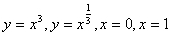 8. 8. 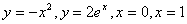
4. 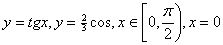 9. 9. 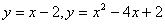
5. 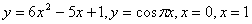 10. 10. 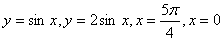
ЛАБОРАТОРНАЯ РАБОТА №5.
Тема. Построение графиков функций.
Цель. Познакомиться с основными действиями при создании графика в
Mathcad. Научиться строить декартов график, графики поверхности, полярные
графики.
Краткие сведения.
I.Основные действия при создании графика.
Чтобы создать график, необходимо проверить следующие операции:
Ø Предварительно определить аргумент и функцию аргумента, для
которой будет строиться график. Аргумент задается диапазонной переменной, а
функция аргумента – функцией пользователя.
Например: х:=0,0.1..π
Y(x):=sin(x)
Ø Щелкнуть мышью там, где нужно создать график.
Ø Выбрать Декартов график из меню Графика. При этом
на экране появится «заготовка» графика с шестью полями ввода, по три на каждой
оси.
Ø Чтобы увидеть график, необходимо заполнить пустые поля:
- Пустое поле в середине горизонтальной оси предназначено для
независимой переменной графика. Нужно ввести в это пустое поле дискретную
переменную, переменную с индексом или любое выражение, содержащее дискретную
переменную.
- Пустое поле в середине вертикальной оси содержит выражение, график
которого нужно построить. Нужно ввести в это пустое поле дискретную
переменную или любое выражение, содержащее дискретную переменную, находящуюся
на горизонтальной оси.
- Другие 4 пустые поля могут использоваться, чтобы отменить
автоматический выбор границ на осях координат в Mathcad.
- Нажать <Enter>. В указанном прямоугольнике появляется график
функции.
Для того, чтобы вывести функцию на график необходимо сделать следующее:
× Напечатать выражение, график которого нужно получить, в среднее поле
на оси ординат и напечатать х в среднем поле на оси абсцисс.
Можно также определить функцию f(x) и поместить ее в среднее пустое поле оси
ординат. Это особенно полезно для функций, представляемых громоздким
выражением.
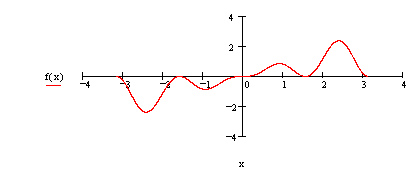
ПРИМЕР 1. Построить график функции 
Решение:
Определим аргумент и функцию аргумента, для которой будет строиться график.
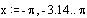

Построим график этой функции.
III. Размещение нескольких графиков на чертеже.
Можно построить несколько кривых на одном и том же чертеже – для этого
достаточно определить их и перечислить в виде списка в шаблоне графика.
График может содержать несколько выражений по оси ординат в зависимости от
одного выражения по оси ординат, согласованных с соответствующими выражениями
по оси абсцисс.
Например, чтобы представить графически несколько выражений по оси ординат
относительно одного выражения по оси абсцисс, необходимо:
× Вести первое выражение для оси ординат, сопровождаемое запятой.
Непосредственно под первым выражением появится пустое поле.
× Ввести в это пустое поле второе выражение, сопровождаемое другой
запятой, чтобы получить другое пустое поле и т.д.
Помните! Все выражения должны использовать одну и ту же дискретную переменную.
Можно построить несколько независимых кривых на одном чертеже. Для этого
необходимо:
× Ввести два или более выражения, отделяемых запятыми на оси абсцисс,
и то же самое число выражений на оси ординат. Mathcad согласует выражения
попарно – первое выражение оси абсцисс с первым выражением оси ординат, второе
со вторым и т.д. Затем рисуется график каждой пары.
Помните! Каждая согласованная пара выражений должна
использовать одну дискретную переменную. Дискретная переменная для одной
согласованной пары не должна быть дискретной переменной для других пар.
ПРИМЕР 2 Построить графики трех функций,зависящих от одной переменной х, в
пределах одного графического блока:
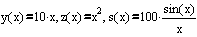
Решение.
Определим аргумент и функции аргумента, для которых будут строиться графики.
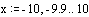
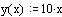
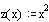
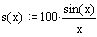
Построим графики данных функций.
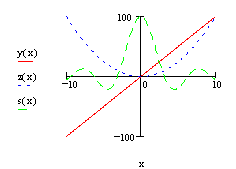
IV. Построение графиков поверхностей.
Трехмерные графики в Mathcad отображают графически матрицы значений.
Чтобы создать график поверхности, необходимо:
× Определить матрицу значений, которую необходимо отобразить
графически. Mathcad будет использовать номер строки и столбца матрицы в
качестве координат по осям X и Y. Элементы матрицы будут представлены на
графике как высоты выше или ниже плоскости X-Y.
× Выбрать График поверхности из меню Графика. Mathcad
покажет рамку с одним полем ввода.
× Напечатать имя матрицы в этом поле. Затем нажать клавишу [F9] или, в
автоматическом режиме, щелкнуть мышью вне выделенной графической области.
ПРИМЕР 3. Построить график поверхности f(x,y)=sin(x+y)
Определим функцию двух переменных:

Допустим, что по осям x и y необходимо 20 точек. Определим дискретные
аргументы i и j, чтобы индексировать эти точки.
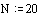 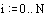 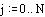
Определим x и y как равномерно располагаемые точки на осях X и Y.
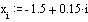 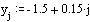
Заполним матрицу М значениями F(x , y )
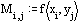
Выберем График поверхности из меню Графика. Напечатаем М в
поле ввода и щелкнем вне графической области.
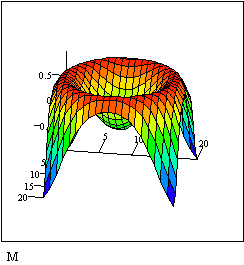
V. Построение полярного графика.
Для отображения функций, которые неудобно воспроизводить в декартовых
координатах, можно строить полярные графики.
Чтобы создать график в полярных координатах, необходимо:
× Выбрать Полярный график из меню Графика. Mathcad
показывает круг с четырьмя полями ввода.
× Выше области графика определить угол Q и функцию угла R(Q).
× Поле ввода внизу предназначено для угловой переменной графика.
Ввести туда дискретную переменную или любое выражение, включающее дискретную
переменную.
× Поле ввода слева должно содержать выражение для радиуса.
× Два поля ввода справа предназначены для верхнего и нижнего граничных
значений радиуса. Mathcad заполняет эти поля по умолчанию.
В Mathcad полярные графики рисуются путем замены R и Q на декартовы
координаты x и y с использованием стандартных преобразований x=Rcos(Q) и
y=Rsin(Q). Предполагается, что R и Q могут принимать и положительные, и
отрицательные значения.
ПРИМЕР 4. Построить график функции R(Q)=cos(Q)+1
Определим приращение для Q:
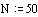
Определим Q как дискретный аргумент с заданным приращением:
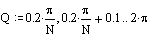
Определим R(Q) как функцию Q:
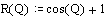
Отобразим график R(Q) в полярных координатах.
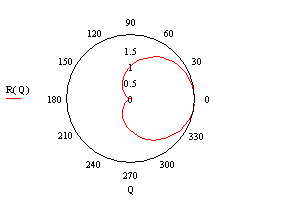
Помните! Mathcad не обрабатывает график, пока вы не нажмете
[F9], или, в автоматическом режиме, не щелкните мышью вне области графика.
Задания для самостоятельного выполнения.
Задание 1.
Построить график функции.
1. 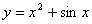 5. 5. 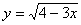 9. 9. 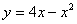
2. 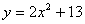  6. 6. 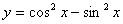 10. 10. 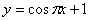
3. 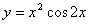 7. 7. 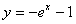
4. 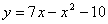 8. 8. 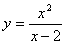
Задание 2. Построить графики двух функций, зависящих от одной переменной.
1. 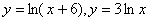 6. 6. 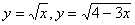
2. 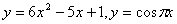 7. 7. 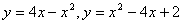
3. 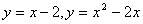 8. 8. 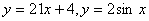
4. 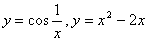 9. 9. 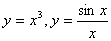
5. 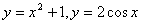 10. 10. 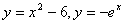
Задание 3. Построить график поверхности.
1. 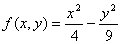 5. 5. 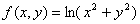 9. 9. 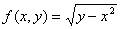
2. 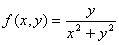 6. 6. 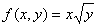 10. 10. 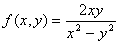
3. 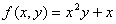 7. 7. 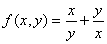
4. 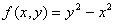 8. 8. 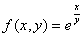
Задание 4. Построить график в полярных координатах.
1. 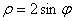 5. 5. 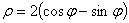 9. 9. 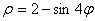
2. 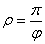 6. 6. 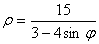 10. 10. 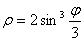
3. 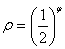 7. 7. 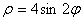
4. 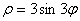 8. 8. 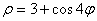
ЛАБОРАТОРНАЯ РАБОТА №6.
Тема. Программирование в Mathcad.
Цель. Познакомиться с возможностями программирования, научиться
создавать программы и решать задачи при помощи программ.
Краткие сведения.
I. Создание программ.
Для решения тех проблем, которые не могут быть реализованы стандартными
средствами, в системе Mathcad предусмотрена возможность написания небольших
программ. Программы в Mathcad являются частным случаем выражений пакета
Mathcad.
Для написания программ используется программная палитра, которая вызывается
кнопкой панели управления. Имеется 10 операторов, из которых строится
программа.
Создание программы начинается с кнопки AddLine. Появится вертикальная линия,
которая играет роль операторных скобок. Справа от вертикальной линии находятся
поля ввода для занесения операторов. Операторы вводятся соответствующей кнопкой
на программной палитре. Поля ввода для дополнительных операторов открываются с
помощью щелчка по кнопке «AddLine». Чтобы исключить лишнее поле ввода, его
нужно выделить и нажать клавишу <DEL>.
Вместо оператора присваивания :=, в программах пользуются оператором
локального присваивания ←. В качестве результата работы Mathcad
возвращает значение. Этим значением является значение последнего выражения,
выполненного программой.
ПРИМЕР 1. Найти один из корней квадратного уравнения 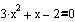
Решение.
Определим коэффициенты и свободный член уравнения:
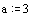  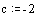
Найдем один из корней уравнения:
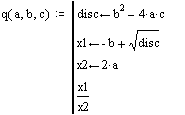
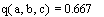
II. Условные операторы.
Могут встретиться случаи, в которых какой-нибудь оператор нужно выполнить только
в случае выполнения некоего условия. Этого можно добиться с помощью условного
оператора «if».
После нажатия на клавишу «if» появится два поля ввода. Правое поле ввода
предназначено для выражения, которое должно выполняться. Левое поле ввода
предназначено для значения, которое будет иметь выражение, если логическое
выражение в правом поле истинно.
III. Циклы.
При программировании появляется возможность многократного выполнения некоторой
последовательности операторов в цикле. Mathcad предлагает 2 вида циклов,
отличающихся по способу определения условия завершения цикла: for или
while.
Цикл «while».
Цикл данного типа используют, если цикл должен завершиться по выполнении
некоторого условия, причем момент выполнения этого условия заранее не
известен.
Чтобы записать цикл типа while, нужно:
× Щелкнуть по кнопке «while» в панели программирования.
× Напечатать условие выполнения в верхнем поле ввода. Обычно это –
логическое выражение.
× Записать в оставшемся поле ввода выражение, подлежащее
повторяющемуся вычислению.
Обнаружив заголовок цикла типа while, Mathcad проверяет условие цикла. Если
оно истинно, то Mathcad выполняет тело цикла и снова проверяет условие. Если
оно ложно, то Mathcad заканчивает выполнение цикла.
Циклы «for».
Цикл данного типа используют, если заранее точно известно необходимое число
выполнений цикла. Число выполнений определяется переменной цикла, задаваемой
в его начале.
Для создания цикла типа for, необходимо:
× Щелкнуть по копке «for» на панели программирования.
× Напечатать в поле ввода слева от знака 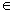 имя переменной цикла. имя переменной цикла.
× Ввести в поле справа от знака 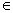
диапазон значений, в котором должна изменяться переменная цикла. Форма задания
диапазона в точности такая же, как и для дискретного аргумента.
× В оставшееся поле ввода впечатать выражение, подлежащее
повторяющимся вычислениям. Обычно оно включает в себя переменную цикла.
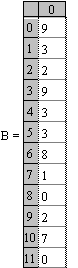
ПРИМЕР 2.
Дан ребус Каждой букве соответствует определенная
цифра.
Восстановить пример.
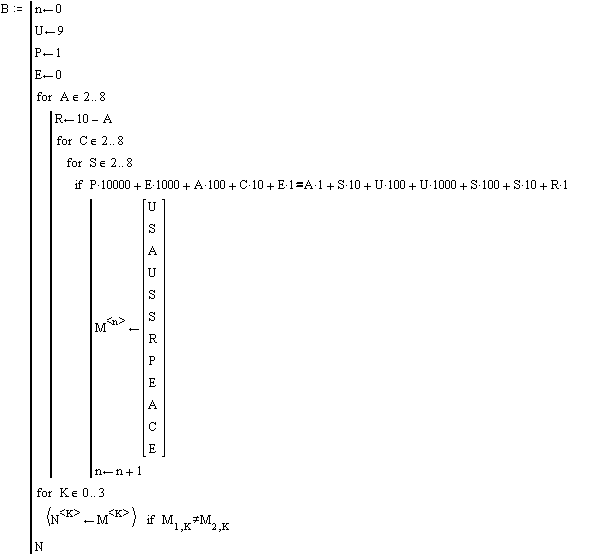
Задачи для самостоятельного выполнения.
1. В одном районе расположены четыре населенных пункта. По территории
района проходит железная дорога. По просьбе жителей района планируется
построить железнодорожную станцию и проложить дороги от нее до населенного
пункта. Требуется определить наиболее удобное расположение железнодорожной
станции. (Место для станции надо выбрать так, чтобы наибольшее из расстояний
от нее до населенных пунктов было как можно меньше.
2. Две моторные лодки равномерно двигались по реке в направлении к озеру,
в которое река впадает. Поравнявшись, они начали двигаться равноускоренно.
Какая из лодок раньше дойдет до озера?
3. На заданном расстоянии от пушки находится стена. Известны угол наклона
пушки и начальная скорость снаряда. Попадет ли снаряд в стену?
4. На узкой улице внезапно заклинило тормоза у «Волги». В результате
немедленно образовалась «пробка». Шофер стоящего сзади грузовика, у которого
лопнуло терпение, предложил помочь убрать «Волгу» с проезжей части дороги,
оттащив ее на обочину с помощью троса. Удастся ли оттащить «Волгу»?
5. Расположенный на берегу реки металлургический завод осуществил сброс
сточных вод, в результате чего концентрация вредных веществ в реке резко
увеличилась. С течением времени эта концентрация, естественно, уменьшается.
Требуется сообщить, каков будет уровень загрязнения реки через сутки, двое
суток и т.д. до тех пор, пока концентрация не станет меньше предельно
допустимой.
6. Органами милиции задержан грузовик с помидорами, похищенными на
овощной базе. В городе всего четыре овощные базы, каждая из них получает
помидоры из своего сельскохозяйственного района. Определить, с какой базы
были вывезены помидоры. Расследование осложняется тем, что помидоры на всех
базах одного сорта.
7. Бетон, производимый на заводах А и В, нужно развозить по трем
стройплощадкам: С1, С2 и С3. Известны потребности стройплощадок в бетоне,
запасы бетона на каждом заводе и затраты на перевозку 1 т бетона от каждого
завода до каждой стройплощадки. Требуется составить такой план перевозок,
который обеспечивал бы наименьшие затраты.
8. Для полива трех полей колхоз использует насосную станцию. На первое
поле требуется подать не менее 200 кубометров воды в сутки, на второе – не
менее 300, на третье не менее 350. В распоряжении колхоза 1200 кубометров
воды в сутки. Стоимость подачи q кубометров воды на первое поле 1570q р., на
второе поле 1720q р., на третье 1930q р. Сколько кубометров воды надо подать
на каждое поле, чтобы затраты были наименьшими?
9. Для производства вакцины на заводе планируется выращивать культуру
бактерий. Известно, что если масса бактерий – х г, то через день она
увеличится на (a-bx)x г, где коэффициенты a и b зависят от вида бактерий. Как
изменяется масса бактерий через 1,2,3,.,365 дней (до конца года)?
10. На острове живут зайцы и волки. Экологи установили такую закономерность:
если в начале года количество зайцев равно х, а количество волков – у, то
через год число зайцев будет равно х+(4-0,001у-0,0001х)х, а число волков
будет равно у+(-0,03+0,003х)у. Сколько зайцев и волков будет на острове через
год, два, три и т.д.? При каких начальных значениях х и у на острове исчезнут
волки и зайцы?
2.4. Методы и организационные формы обучения
В соответствии с задачами профильного обучения информатике в старших классах,
обучение должно быть направлено, в первую очередь, на интеллектуальное
развитие школьников. В условиях профильного обучения старшеклассников
создается реальная возможность развития творческих способностей учащихся,
подготовки их к будущей профессиональной деятельности. Поэтому в процессе
обучения следует использовать не только репродуктивные методы, но и методы,
формирующие способность самостоятельного приобретения знаний, потребность к
самообразованию. Это подчеркивается в концепции общего среднего образования:
«Объяснительно-иллюстрированных и репродуктивных методов недостаточно, чтобы
обеспечить субъектно-личностный характер обучения и вызвать познавательную
активность ученика».(6).
Процесс обучения невозможен без организации и осуществляется в определенных
формах. Традиционно основной формой обучения является урок. Он обеспечивает
планомерную познавательную деятельность группы определенного возраста,
состава и уровня подготовки, направленную на решение поставленных задач.
Использование на уроках персональных компьютеров и НИТ дают возможность
педагогам качественно изменить содержание, методы и организационные формы
обучения, способствуют раскрытию, сохранению и развитию индивидуальных
способностей учащихся, обеспечивают активное и комплексное изучение явлений
действительности.
Особенности изучения математических пакетов позволяют использовать различные
методы и организационные формы обучения. При обучении по предлагаемому курсу
можно использовать такие виды уроков, как уроки сообщения новой информации
(уроки-лекции) и уроки развития и закрепления умений и навыков (лабораторные
работы). На практике также широко распространены комбинированные уроки. Как
известно такие уроки, обеспечивая многократную смену видов деятельности,
создают условия для быстрого применения новых знаний, возможность реализации
индивидуального подхода в обучении.
На уроках-лекциях учитель ясно объясняет материал и проверяет правильность
усвоения учениками его основных моментов. Причем это не монолог учителя, не
традиционные объяснения и опросы, а беседа и обсуждение новых понятий. Такой
урок должен включать демонстрацию компьютерной программы (в нашем курсе –
математические пакеты). Учащиеся наблюдают за действиями учителя. Большое
внимание должно уделяться наглядности, что позволит преодолеть специфику
компьютерной предметности, не допустить смещения в восприятии реального и
компьютерного миров, вытеснения первого последним. Учащимся могут быть
предложены проблемная ситуация, логическая задача, решение которой поможет
достижению цели урока, различные задания для подготовки учащихся к восприятию
новой программы, а следовательно эффективного ее освоения.
Лабораторные работы по курсу могут представлять собой период самостоятельной,
но синхронной работы учащихся под руководством учителя. Эта работа направлена
либо на его освоение или закрепление материала, объясненного учителем либо на
проверку усвоения полученного знания или операционного навыка. Роль учителя
во время такой работы – обеспечение синхронности действий учащихся и оказание
экстренной помощи по инициативе учеников. Лабораторные работы могут также
представлять собой практическую работу учащихся с компьютером по
индивидуальным заданиям, что требует синтеза знаний и умений по пройденному
материалу. В разработанных нами лабораторных занятиях учащимся предлагаются
индивидуальные задания, которые они самостоятельно выполняют в течение
одного-двух уроков (в зависимости от степени сложности материала).
При обучении могут применяться и объяснительно-иллюстративные методы обучения
и методы проблемного обучения. Особое место занимает метод учебных проектов.
При этом деятельность учащихся может быть организована как в форме
индивидуальной работы учащихся с компьютером, так и групповой.
Данный курс является курсом подготовки пользователя компьютера. Подготовить
пользователя по информационным технологиям означает привить ученику навыки
практической деятельности не только при работе с конкретным программным
продуктом, но и при освоении нового средства. Именно одним из подходов к
решению этой задачи и является метод исследовательских проектов. Учебные
проекты выступают как форма организации творческой работы школьника по
решению практических задач и нацелены на многие проблемы меж предметного и
междисциплинарного профилей.
Опираясь на результаты психолого-педагогических исследований о роли задач в
учебном процессе, отметим, что задача в разрабатываемом курсе является
основным средством обучения. Одни авторы утверждают, что всякое сознательное
человеческое действие является решением задач. Другие отмечают, что любая
мыслительная деятельность человека есть решение либо теоретических, либо
практических задач. Задачи не только являются источником информации,
импульсом к последующей деятельности учащихся, но и учат их учиться.
Усвоение материала курса может осуществляться на разных уровнях с учетом
индивидуальных особенностей учащихся. А также различной ориентации на
использование математических пакетов в своей будущей профессии. В связи с
этим, преподавание курса может быть направлено на усвоение материала на более
высоком уровне, чем указано в программе.
Так, кроме знаний и умений для обязательного усвоения материала фрагмента
курса – «Пакет для научных расчетов Mathcad» учащиеся могут знать и уметь:
1) После изучения раздела «Язык математических вычислений пакета»:
- иметь представление о работе с документами в Mathcad:
редактирование формул, документы и окна, текст, форматирование выражений и
результатов;
- уметь управлять вычислениями, копировать числовые результаты;
- уметь вычислять с единицами измерений, отображать единицы измерений
результатов, изменять наименования размерностей;
- создавать вектора или матрицы; вычислять с массивами, выполнять
параллельные вычисления.
- Уметь пользоваться пакетами Функций Mathcad;
- Уметь выполнять символьные вычисления.
2) После изучения раздела «Графические возможности пакета»:
- уметь форматировать оси, отдельные кривые;
- уметь изменять масштабы графиков;
- уметь создавать карты линий уровня и форматировать их;
- уметь создавать трехмерные гистограммы и форматировать их;
- уметь создавать точечные графики и форматировать их;
- уметь импортировать в рабочий документ графические изображения из
различных источников.
Исходя из того, что ученики старших классов проявляют особый интерес к
овладению именно теми знаниями и умениями, которые пригодятся им в будущей
профессиональной деятельности, обучение лучше всего строить так, чтобы
показать применимость знаний и умений, необходимых для усвоения согласно
целям обучения, на практике. Тем более предполагается, что у учащихся
профильных классов уже сформирована потребность изучать интересующий их
материал на современном уровне, т.е. с применением современных технологий,
которые используются в выбранной ими профессии.
В заключении отметим, что изучение в специализированных классах фрагмента
курса «Математический пакет для научных расчетов «Mathcad»» необходимо и
доступно для школьников.
Заключение
В процессе написания дипломной работы была проанализирована
теоретическая и научно-методическая литература по данной теме. Обобщая
полученные сведения, была сформулирована теоретическая и научно-методическая
литература по данной теме. Обобщая полученные сведения, была сформулирована
гипотеза работы и поставлены задачи для ее подтверждения.
В ходе работы над дипломным проектом было сделано следующее:
- определено значение дифференциации обучения информатике;
- выявлена сущность профильной дифференциации обучения;
- обосновано содержание фрагмента прикладного профильного курса
«Новые информационные технологии» для специализированных классов (с
углубленным изучением математики);
- определены цель и основные задачи данного курса;
- разработано содержание фрагмента прикладного профильного курса –
«Математический пакет для научных расчетов «Mathcad»»;
- составлено тематическое планирование данного фрагмента курса;
- разработаны лабораторно-практические занятия по данному фрагменту
курса;
- рассмотрены методы и организационные формы обучения информатике;
- разработан материал для учащихся к лабораторным работам с
вариантами заданий для самостоятельного выполнения.
Разработанные лабораторно-практические занятия по курсу «Математический пакет
для научных расчетов «Mathcad»» могут быть использованы в практике работы
учителей. Это будет служить не только расширению и углублению теоретических
знаний, умений и навыков школьников по математике, но предполагает и
практическую подготовку, усиливающую профориентационную направленность
обучения математике с использованием математических пакетов (в частности,
пакета Mathcad).
Литература
1. Дьяконов В.П. Система Mathcad: Справочник .- М.: Радио и связь,1993,-
128с.
2. Дьяконов В.П. Автоматизация математических расчетов с помощью системы
Mathcad.// Мир ПК.- 1991.- №8.
3. Дьяконов В.П. Справочник по Mathcad PLUS 6.0 PRO.- М.: СК – ПРЕСС, 1997.
4. Захарова Т. Профильная дифференциация обучения информатике на старшей
ступени школы: Монография. - М, 1997, 212с.
5. Кузнецов А.А. О разработке стандарта школьного образования по
информатике.// Информатика и образование. - 1994.- №1.
6. Концепция общего среднего образования как базового в единой системе
непрерывного образования. - М.: АПН СССР, 1988.- 50с.
7. Лапчик М.П. Методика преподавания информатики: Учебное пособие для
студентов физико-математических факультетов пединститутов.
- Свердловск: Пед. Институт, 1987.- 152с.
8. Математический пакет Derive.// Компьютер Пресс. - 1998.- №3.
9. Мануйлов В.Г. Основы информационных технологий.// Информатика и
образование. - 1995.- №3.
10. Mathcad 2.5 – математический пакет для научных расчетов: Методическое
пособие для студентов физико-математического факультета./Сост. А.В. Гуторов.-
Нижний Тагил, 1997.- 59с.
11. Mathcad 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде
Windows 95.- М.: Филинъ, 1996.- 712с.
12. Монахов В.М. и др. Проблема дифференциации обучения в средней школе:
Методические рекомендации учителю о дифференцированном обучении как средстве
индивидуализации развития личности школьника./Под ред. К.Н. Мешалкиной, В.А.
Орлова. - М.,1990.
13. Национальный доклад Российской Федерации «Политика в области образования
и новые информационные технологии».- М., 1996.
14. Основные компоненты содержания информатики в общеобразовательных
учреждениях.// Информатика и образование. - 1995.- №4.
15. Очков В.Ф. Mathcad PLUS 6.0 для студентов и инженеров. - М.: Компьютер
Пресс, 1996.
16. Потемкин В.Г. Система Matlab: Справочное пособие. - М.: Диалог – МИФИ,
1997.- 350с.
17. Программно-методические материалы: Информатика. 1-11 классы. - 96с.
18. 15 практических занятий с Mathcad 7.0: Методические указания к выполнению
практикума по курсу «Вычислительная техника»./Сост. Литвиненко Н.А.-
Екатеринбург: УГТУ, 1998.- 36с.
19. Современные проблемы методики преподавания математики и информатики:
Материалы I Сибирских методических Чтений. - Омск: ОМГУ, 1995.
20. Степанова И.Ю. Программа спецкурса «Элементы языка ПРОЛОГ»./ Информатика
в средней школе. Сборник методических материалов. Сост. Н.И. Пак. - Омск:
Издательство Омского пединститута, 1993.
21. Унт И. Индивидуализация и дифференциация обучения. - М.: Педагогика,
1990.- 192с.
22. Шахмаев Н.М. Учителю о дифференцированном обучении: Методические
рекомендации. - М.: НИИ ОП, 1989.- 65с.
23. Швецкий М.В. Методическая система фундаментальной подготовки будущих
учителей информатики в педагогическом вузе в условиях двухступенчатого
образования: Диссертация доктора педагогических наук.
- Санкт-Петербург, 1994,- 480с.
24. Якиманская И.С. Знания и мышление школьника. - М.: Знание, 1985.- 78с.
Страницы: 1, 2, 3
|

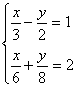 9.
9. 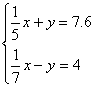
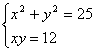 7.
7. 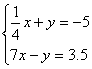

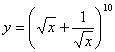
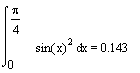

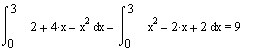 (кв.ед.)
(кв.ед.)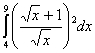 6.
6. 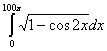 10.
10.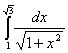
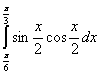 7.
7.