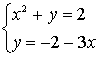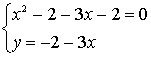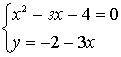|
|
Диплом: Самостоятельная работа как средство обучения решению уравнений в 5-9 классах
В курсе математики старших классов учащиеся сталкиваются с новыми классами
уравнений, систем или с углубленным изучением уже известных классов. Однако
это мало влияет на уже сформированную систему; они дополняют ее новым
фактическим содержанием, не меняя сложившиеся связи, соединяющие различные
классы. На этом, более высоком уровне владения материалом связи становятся
намного более освоенными, так что учащиеся в процессе выполнения заданий
могут самостоятельно их восстанавливать.
§ 5. Методика изучения основных классов уравнений и их систем.
1. Линейные уравнения с одним неизвестным.
Этот класс уравнений — первый в курсе алгебры, поэтому от характера его
изучения в значительной мере зависят особенности организации всего
последующего изучения линии уравнений. При изучении этого класса уравнений,
помимо его непосредственного выделения и описания, приходится останавливаться
на вопросах, относящихся к формированию общего понятия об уравнении, вводить
терминологию.
В § 2 были приведены различные взгляды на содержание понятия уравнения. Было
отмечено, что каждый из них имеет определенную ценность в развертывании
содержания курса алгебры. Поскольку рассматриваемый класс является первым в
курсе, указанные взгляды тем или иным способом должны найти место на этом
этапе изучения материала линии уравнений и неравенств.
Первая методическая задача, с которой учитель сталкивается, приступая к
изложению этой темы, состоит в выделении формальной части понятия уравнений из
той содержательной ситуации, в которой оно возникает. В качестве такой ситуации
обычно выступает несложная текстовая задача, решение которой алгебраическим
методом приводит к уравнению первой степени с одним неизвестным. Учителю
следует обратить внимание учащихся на основной метод, примененный в решении
задачи,— переход к ее алгебраической модели, общий вид которой
f{x)=g(x), где f u g — некоторые выражения, содержащие
неизвестное х. Далее, на основе анализа конкретно полученной формулы
учитель приводит формулировку общего понятия уравнения, принятую в учебнике, и
вводит (или напоминает) связанные с ним термины. Вслед за этим нужно обратить
внимание на те формальные характеристики составленного уравнения, которые уже
непосредственно приводят к описанию изучаемого конкретного класса уравнений.
В различных учебниках применяется разная терминология, относящаяся, по
существу, к одному и тому же классу уравнений. В этом отношении необходимо
быть чрезвычайно внимательным и употреблять только те термины, которые
введены в учебнике, причем именно в том смысле, который им придается.
Опишем несколько подходов к выделению первого изучаемого в курсе алгебры
класса уравнений.
В учебнике для для 6 класса средней школы Макарычева это линейные уравнения с
одной переменной, т. е. уравнения вида ах=b, где х —
переменная, а и b — числа. Естественно, что это определение
выделяет очень узкий класс уравнений, недостаточный для решения самых простых
задач. Какую роль он выполняет? Это роль двоякая. Во-первых, уравнения этого
класса просто решаются, причем так описанный класс допускает полное
исследование (что и осуществляется в учебнике). Во-вторых, запись уравнений из
этого класса играет роль образца, к которому могут быть сведены посредством
простейших преобразований уравнения более широкого класса. Большая часть
времени, отводимого на изучение линейных уравнений по этому учебнику,
используется именно на то, чтобы сформировать навыки сведения к линейным других
уравнений, не входящих в этот класс.
В [20][2] вводится и рассматривается класс
уравнений, названный по-иному — уравнения первой степени с одним неизвестным. К
особенностям введения этого класса следует отнести то, что явного определения
он не получает: определение заменяется описанием и иллюстрацией несколькими
примерами. Предполагается, что в итоге их рассмотрения учащиеся получат
достаточно ясное представление об объеме понятия. Основное внимание уделяется
изложению правил последовательного преобразования уравнения ко все более
простому виду. Фактически при этом приходят к уравнению ах=b. Этот
последний класс уравнений явно не выделяется, но на примерах рассматриваются
все возможные случаи решения уравнений из него. Такой подход позволяет
сконцентрировать внимание непосредственно на алгоритмах решения уравнений.
В [159][3] также вводится понятие уравнения
первой степени с одним неизвестным и объясняется алгоритм его решения. В
отличие от [20] здесь дано явное определение: «Алгебраическое уравнение от
одного неизвестного называется уравнением первой степени, если обе его части
являются многочленами первой степени относительно неизвестного». По поводу
этого определения следует сказать, что по смыслу понятия степени многочлена,
введенного в этом учебнике, оно относится к конкретной записи многочлена без
приведения подобных членов; например, многочлен 2х+ 1 —(2х—3) — первой степени.
В [129][4] в системе изучения присутствуют
оба понятия: и линейного уравнения с одним неизвестным, и уравнения первой
степени. Первое из них описывает широкий класс уравнений (левая и правая части
уравнения — нуль или многочлены не выше первой степени), а второе—более узкий
(уравнение вида kx+b=0, k¹0).
Выделение подкласса уравнений первой степени в классе линейных уравнений в
принципе может облегчить изложение этого класса. В частности, введение двух
терминов (линейное уравнение, уравнение первой степени) позволяет четче
описать сам процесс решения. Однако при этом возникает необходимость в
усвоении двух, а не одного термина. Точно так же указание явного определения
изучаемого понятия по сравнению с описанием имеет преимущество большей
четкости, но предъявляет более высокие требования к развитию логического
мышления учащихся.
Охарактеризованные четыре варианта изложения теории уравнений, имеющих вид
ax + b == сх + d, свидетельствуют о том, что эта
теория допускает несколько различных по стилю и методике изучения
развертывании. Можно (как это сделано в первом и четвертом случаях)
сконцентрировать внимание на выделении более узкого класса, играющего роль
«канонического вида», к которому приводятся данные уравнения; но можно (как во
втором и третьем случаях) обойтись и без этого, а сразу изучать способы решения
уравнений общего класса, используя изученные типы преобразований уравнений.
Точно так же можно с разной степенью выявленности описывать вводимые термины:
четким определением или же посредством описания.
Несмотря на наличие таких разных подходов к введению первого класса
уравнений, значительная часть методики его изучения одинакова при любом из
них. Это объясняется прежде всего тем, что основной целью изучения в данном
случае всегда является освоение правил решения уравнений данного класса,
образующих сравнительно компактную систему и относящихся исключительно к
преобразованиям буквенно-числовых выражений. В последнем отношении
рассматриваемый класс сильно отличается от большинства других классов, в
изучении которых определенную, а иногда значительную роль играют логические,
графические, вычислительные компоненты.
При изучении этого класса уравнений учащиеся подходят к осознанию того, что
уравнения, с первого взгляда мало отличные друг от друга, могут резко
различаться по количеству корней. Это ответственный момент, один из самых
существенных в изучении всего курса алгебры, поскольку при этом учащиеся
впервые сталкиваются с необходимостью теоретического осмысления именно
класса уравнений, а не каждого уравнения в отдельности.
Конкретные способы изложения материала, относящегося к исследованию, могут
быть различными. Зависят они в первую очередь от стиля выделения этого
класса. Если он выделяется явным определением, то и результаты исследования
формулируются в виде четкой системы условий, при выполнении которых имеет
место один из трех возможных случаев. Если же этот класс уравнений выделяется
посредством описания, то реализация каждого из этих случаев показывается на
примерах, но общего обоснования не дается.
Отметим еще, что рассматриваемый класс является единственным, для которого в
современной методике есть разные подходы к проведению исследований. Для
каждого из остальных классов уравнений, неравенств, систем исследование
проводится, по существу, одинаково при любом построении курса алгебры. Именно
те классы уравнений, неравенств, систем, алгоритмы решения которых
заучиваются при усвоении материала, исследуются аналогично первому способу;
для тех классов, где результирующих формул для получения ответа не
указывается, используется второй способ.
В итоге тематического изучения первого класса уравнений учащиеся должны
овладеть: алгоритмом решения уравнений данного класса; умением применять
результаты исследования уравнений данного класса; основными понятиями общей
теории уравнении;
применением уравнений данного класса к решению текстовых задач.
2. Системы двух линейных уравнений с двумя неизвестными.
С помощью линейных уравнений с одним неизвестным можно решать многочисленные
.задачи, в которых либо имеется только одно неизвестное, либо среди
неизвестных можно указать одно «ведущее», через которое выражаются остальные.
Но многие ситуации описываются несколькими параметрами, вообще говоря,
равноправными друг другу; эти ситуации требуют разработки новых
алгебраических средств их изучения. В качестве одного из таких средств в
курсе алгебры выступает класс систем двух линейных уравнений, с двумя
неизвестными.
Приведенное рассуждение может быть положено в основу методики изучения
указанного класса. Такой способ введения подчеркивает прикладную значимость
уравнений с двумя неизвестными, однако изучение этого класса требует введения
обширной совокупности формальных понятий и методов, поэтому отмеченная схема
изложения, в которой проводится содержательная мотивировка данного класса, не
единственный способ изложения этого материала.
Изложение темы можно начать с рассмотрения понятий, входящих в качестве
компонентов в понятие системы линейных уравнений с двумя неизвестными; их
соединение формирует представление о данном классе. Эти компоненты таковы:
представление о конъюнкции логических условий, которое формализуется в
понятии системы уравнений; представление о наличии в составе логического
условия двух переменных, представление о линейном уравнении с двумя
неизвестными, непосредственно связанное с данным классом систем.
Рассмотрим эти компоненты подробнее. Полезность изучения понятия уравнения с
двумя неизвестными перед введением понятия о системе уравнений заключается
в том, что при этом могут быть рассмотрены два важных в дальнейшем вопроса:
выражение одного из неизвестных через другое (это преобразование используется
при изучении метода подстановки) и введение понятия графика уравнения с двумя
неизвестными.
Существенно новым представлением, которое получают учащиеся при изучении этой
темы, является представление о том, что решением уравнения с двумя
неизвестными служит не число, а упорядоченная пара чисел. Вторым
представлением, резко расширяющим кругозор учащихся, служит то, что множество
решений уравнения с двумя неизвестными, как правило, бесконечно и его
изображение на координатной плоскости — некоторая линия.
Изучение этой темы может рассматриваться как определенный мостик, связывающий
понятие функции и понятие уравнения с двумя неизвестными: с одной стороны,
уравнение с двумя неизвестными, в котором одно из них выражено через другое,
по виду формулы совпадает с функцией; с другой — оказывается, что один и тот
же геометрический образ является и графиком уравнения, и графиком функции.
Эти первые представления в дальнейшем подвергаются неоднократному уточнению и
переосмысливанию, но уже и в таком несовершенном виде они с успехом
используются при изучении систем уравнений.
Тема «Уравнение с двумя неизвестными» в случае наличия ее в курсе изучается
недолго. Цель ее изучения состоит скорее во введении новых представлений, чем
в развитии навыков.
Непосредственно за ней или на ее месте рассматривается тема «Линейные уравнения
с двумя неизвестными». Этот класс изучается детальнее. Здесь необходимо
приобрести навыки перехода от линейного уравнения ах+bу=с к уравнению
y=kx+b или x=k1y+b1. Кроме того, требуется
усвоить факт: график линейного уравнения ах + bу= с, где а¹0
или b¹0, есть прямая линия, а также научиться строить график
конкретных линейных уравнений с двумя неизвестными.
Непосредственно перед изучением систем линейных уравнений может быть введено
понятие о системе уравнений с двумя неизвестными. Но здесь необходимы
некоторые уточнения. Понятие системы уравнений в курсе школьной математики
строго определено быть не может из-за отсутствия в нем понятия конъюнкции.
Однако для развития теории уравнений достаточно оказывается формировать
представление о системе уравнений косвенным образом, посредством указания на
цель — нахождение общих решений, двух данных уравнений. Заметим, что общее
понятие о системе уравнений в этот момент и необязательно вводить. Общее
понятие формируется постепенно на основе своего ведущего частного случая —
системы линейных уравнений,— который и составляет непосредственный предмет
изучения. Фактически получается так, что понятие о системе уравнений
формируется у учащихся на основе осмысления понятия «решение уравнения» и
представления о том, что значит решить уравнение. |
Переход к изучению системы двух линейных уравнений с двумя неизвестными
целесообразно осуществить при помощи того же процесса выделения
математических понятий из текстовой задачи, который был использован в
изучении первого класса уравнений. Если реализуемая в учебнике методическая
система не содержит пропедевтики этого понятия, такой подход является
единственно возможным. Однако даже и при наличии подготовки он позволяет
уточнить формальные характеристики вводимого класса систем уравнений и
подчеркнуть некоторые существенные моменты: например, что решением системы
является не одно число, а пара чисел
Основное содержание рассматриваемой темы состоит в изучении двух
алгебраических способов решения таких систем, графического способа решения и
исследования систем этого класса.
Отметим наиболее важные отличия в изучении этого материала от изучения класса
линейных уравнений с одним неизвестным.
Алгоритмы решения систем линейных уравнений намного сложнее алгоритма решения
линейного уравнения с одним неизвестным. Поэтому при их изучении учитель
должен четко указывать последовательность операций, используемых в этих
алгоритмах, а также провести изучение каждого действия. Эти алгоритмы, по
существу, являются первым нетривиальным примером алгоритма в линии уравнений
и неравенств.
В развертывании содержания данной темы используются геометрические
представления, которые не только в ряде мест могут пояснить изложение, но
имеют важное самостоятельное значение. Наиболее принципиальным является их
применение для проведения исследования данного класса систем. Возможны
различные уровни развертывания этого материала — от иллюстраций, поясняющих
смысл различных типов множеств решений, и до использования геометрических
представлений для выведения аналитических условий, определяющих каждый
случай.
Второй, более высокий уровень в современном школьном курсе алгебры обычно не
достигается.
3. Квадратные уравнения.
Для этой темы характерна большая глубина изложения и богатство
устанавливаемых с ее помощью связей в обучении, логическая обоснованность
изложения. Поэтому она занимает исключительное положение в линии уравнений и
неравенств. К изучению этой темы учащиеся приступают, уже накопив
определенный опыт, владея достаточно большим запасом алгебраических и
общематематических представлений, понятий, умений. В значительной мере именно
на материале этой темы осуществляется синтез материала, относящегося к
уравнениям.
Во всех современных школьных учебниках алгебры и термин, и объем понятия
квадратного уравнения одинаковы. Понятие вводится посредством явного
определения, что обязывает организовать работу по усвоению его формальных
признаков. Это тем более необходимо, что соответствующие признаки существенно
используются при построении теории квадратных уравнений, в частности при
выводе формулы корней и в теореме Виета.
Вывод формулы корней квадратного уравнения может быть осуществлен несколькими
различными способами: сразу для общего или сначала для приведенного квадратного
уравнения, сведением к уравнению х2—а=0 или к уравнению
х2=а. Но в любом случае приходится использовать выделение полного
квадрата в трехчлене ах2+bх+с, сводящее уравнение к
двучленному. Выделение последовательности шагов, приводящих к решению
квадратных уравнений, проводится сначала на конкретных примерах.
Необходимым этапом при выводе формулы корней квадратного уравнения служит
исследование, выявляющее три возможных случая: отсутствие корней, наличие
одного или двух корней. При этом вводится дискриминант уравнения. В результате
исследования формулируется вывод: «Если дискриминант квадратного уравнения
ах2+bх+с = 0 отрицателен, то оно не имеет действительных
корней; если дискриминант равен нулю, то имеется один корень, равный - b/2a
; если дискриминант положителен, то уравнение имеет два корня 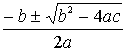 ».
Учитывая этот вывод, решение конкретных квадратных уравнений проводится
следующим образом: сначала вычисляется дискриминант, сравнивается с нулем, и
если он неотрицателен, то применяются формулы для нахождения корней.
В ряде учебников, кроме основной формулы для корней квадратного уравнения ах
2 + bх + с = 0, приводятся еще формулы корней уравнения x2
+px+q=0 или x2+2px+q=0. Иногда использование этих формул
упрощает вычисления, при наличии времени полезно их рассмотреть.
При изучении темы «Квадратные уравнения» рассматриваются и неполные
квадратные уравнения. Обычно они изучаются перед выводом корней общего
квадратного уравнения. Хотя различные виды неполных квадратных уравнении
имеют разные алгоритмы решения, при изучении данной темы необходимо показать,
что общая формула корней применима и для этих случаев.
Важным моментом в изучении квадратных уравнений является рассмотрение теоремы
Виета, которая утверждает наличие зависимости между корнями и коэффициентами
квадратного уравнения. Сложность освоения теоремы Виета связана с несколькими
обстоятельствами. Прежде всего требуется учитывать различие прямой и обратной
теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в
обратной — только два числа, а квадратное уравнение появляется в заключении
теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения
неверной ссылкой на прямую или обратную теорему Виета. Например, при
нахождении корней квадратного уравнения подбором ссылаться нужно на обратную
теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы
распространить теоремы Виета на случай нулевого дискриминанта, приходится
условиться, что в этом случае квадратное уравнение имеет два равных корня.
Удобство такого соглашения проявляется при разложении квадратного трехчлена
на множители.
Владение теорией квадратных уравнений существенно расширяет возможности решения
уравнений методами, изучаемыми в курсе алгебры. Так, прямо сводятся к
квадратным дробно-рациональные уравнения вида
».
Учитывая этот вывод, решение конкретных квадратных уравнений проводится
следующим образом: сначала вычисляется дискриминант, сравнивается с нулем, и
если он неотрицателен, то применяются формулы для нахождения корней.
В ряде учебников, кроме основной формулы для корней квадратного уравнения ах
2 + bх + с = 0, приводятся еще формулы корней уравнения x2
+px+q=0 или x2+2px+q=0. Иногда использование этих формул
упрощает вычисления, при наличии времени полезно их рассмотреть.
При изучении темы «Квадратные уравнения» рассматриваются и неполные
квадратные уравнения. Обычно они изучаются перед выводом корней общего
квадратного уравнения. Хотя различные виды неполных квадратных уравнении
имеют разные алгоритмы решения, при изучении данной темы необходимо показать,
что общая формула корней применима и для этих случаев.
Важным моментом в изучении квадратных уравнений является рассмотрение теоремы
Виета, которая утверждает наличие зависимости между корнями и коэффициентами
квадратного уравнения. Сложность освоения теоремы Виета связана с несколькими
обстоятельствами. Прежде всего требуется учитывать различие прямой и обратной
теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в
обратной — только два числа, а квадратное уравнение появляется в заключении
теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения
неверной ссылкой на прямую или обратную теорему Виета. Например, при
нахождении корней квадратного уравнения подбором ссылаться нужно на обратную
теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы
распространить теоремы Виета на случай нулевого дискриминанта, приходится
условиться, что в этом случае квадратное уравнение имеет два равных корня.
Удобство такого соглашения проявляется при разложении квадратного трехчлена
на множители.
Владение теорией квадратных уравнений существенно расширяет возможности решения
уравнений методами, изучаемыми в курсе алгебры. Так, прямо сводятся к
квадратным дробно-рациональные уравнения вида 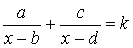 и биквадратные уравнения.
Еще один класс составляют алгебраические уравнения, которые разложением на
множители могут быть сведены к линейному и квадратному уравнениям. Богатство
и разнообразие приемов, имеющихся у учащихся, овладевших сведением различных
уравнений к квадратным, служат необходимой предпосылкой перехода к
завершающему этапу освоения методов решения уравнений. Особенно это
сказывается на приложении к алгебраическому методу решения текстовых задач.
Сюжеты их становятся более разнообразными, возрастает также сложность
перевода на язык математики. В целом можно сказать, что освоение темы
«Квадратные уравнения» поднимает учащихся на качественно новую ступень
овладения содержанием школьной математики.
Глава II. Методико - педагогические основы использования
самостоятельной работы, как средство обучения решению уравнений в 5 - 9
классах.
§ 1. Организация самостоятельной работы при обучения решению уравнений в
5 - 9 классах.
При традиционном способе преподавания учитель часто ставит ученика в
положение объекта передаваемой ему извне информации. Такой постановкой
образовательного процесса учитель искусственно задерживает развитие
познавательной активности ученика, наносит ему большой вред в
интеллектуальном и нравственном отношении.
«Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не
памятью», — эти слова Л. Н. Толстого должны стать смыслом работы учителя.
Самостоятельную деятельность учащихся можно и нужно организовывать на
различных уровнях: от воспроизведения действий по образцу и узнавания
объектов путем их сравнения с известным образцом до составления модели и
алгоритма действий в нестандартных ситуациях.
Учителю Необходимо учитывать, что при составлении заданий для самостоятельной
работы степень сложности должна отвечать учебным возможностям детей.
Переход с одного уровня на другой должен осуществляться постепенно, только
когда учитель будет убежден, что учащийся справится со следующим уровнем
самостоятельности. Иначе в атмосфере спешки и нервозности у ученика возникают
пробелы в знаниях.
Очень важно, чтобы содержание самостоятельной работы, форма и время ее
выполнения отвечали основным целям обучения данной теме на данном этапе.
В то же время учителю нужно знать, что злоупотребление самостоятельной
работой в учебном процессе также вредно, как и ее недооценка. Бывает так, что
учитель включает в урок самостоятельную работу без особой необходимости,
просто ради разнообразия, не продумав ее содержание и форму организации.
Результаты бывают плачевны: или дети не готовы выполнить задание, или не
хватило времени и т. п. А в результате — зря потрачено драгоценное время
урока. Но если, составляя план урока, учитель тщательно продумал место и
время самостоятельной работы; четко определил ее общее содержание, разбил
задания по разным уровням сложности, то она сыграет свою положительную роль.
Поэтому учителю очень важно знать формы и виды самостоятельных работ, их
место в процессе обучения.
Но нельзя забывать, что на успехи ученика огромное влияние оказывает настрой
самого учителя. Здесь очень важен известный психологам эффект Резенталя —
Якобсона. Эти исследователи провели следующий эксперимент: они давали
учителям заведомо неправильную информацию о показателях умственного развития
детей. Как выяснилось, последующие достижения учеников зависели от этой
информации, т. е. от мнения учителя о возможностях ученика. Те дети, которые
воспринимались учителем как более одаренные (хотя таковыми не являлись),
показали большие сдвиги в учебе по сравнению с детьми, которых учитель считал
менее одаренными.
Вот почему так важно умение учителя создать в классе доброжелательную
атмосферу, особенно во время выполнения самостоятельных работ.
В зависимости от целей, которые ставятся перед самостоятельными работами, они
могут быть:
1) обучающими;
2) тренировочными;
3) закрепляющими;
4) повторительными;
5) развивающими;
6) творческими;
7) контрольными.
1 Смысл обучающих самостоятельных работ заключается в
самостоятельном выполнении школьниками данных учителем заданий в ходе
объяснения нового материала. Цель таких работ — развитие интереса к изучаемому
материалу, привлечение внимания каждого ученика к тому, что объясняет учитель.
Здесь сразу выясняется непонятное, выявляются сложные моменты, дают себя знать
пробелы в знаниях, которые мешают прочно усвоить изучаемый материал.
Самостоятельные работы по формированию знаний проводятся на этапе подготовки
к введению нового содержания, а также при непосредственном введении нового
содержания, при первичном закреплении знаний, т. е. сразу после объяснения
нового, когда знания учащихся еще непрочны. Учителю необходимо знать
следующие особенности обучающих самостоятельных работ:
их надо составлять в основном из заданий репродуктивного характера, проверять
немедленно и не ставить за них плохих оценок.
Так как самостоятельные обучающие работы проводятся во время объяснения
нового материала или сразу после объяснения, то их немедленная проверка дает
учителю четкую картину того, что происходит на уроке, какова степень
понимания учащимися нового материала на самом раннем этапе его изучения. Цель
этих работ — не контроль, а обучение, поэтому им следует отводить много
времени на уроке.
Тема: «Линейное уравнение с двумя переменными».
Цель: 1. Дать понятие линейного уравнения с двумя переменными,
решения уравнения с двумя переменными; познакомить со свойствами уравнений с
двумя переменными; закрепить понятие линейного уравнения с одной переменной.
2. Развивать вычислительные навыки, речь, мышление, память.
3. Воспитывать самостоятельность активность , трудолюбие, любовь к математике.
Оборудование: карточку ax+by>c.
Ход урока.
I. Организационное начало урока.
-Здравствуйте, садитесь, сегодня урок алгебры проведу у вас я, зовут меня
Елена Федоровна
II. Сообщение темы и цели.
-Сегодня, на уроке мы познакомимся с уравнениями нового вида - «Линейными
уравнениями с двумя переменными».
III. Актуализация знаний учащихся.
-Посмотрите на доску. Какие из этих уравнений вам уже знакомы?
7х2+3х+5=0 5х+9=54
4х+9у=7 9(х2+6х+2)-8=30
x2/3+y2/2=1 4(х+2)+1=х+18.
-А как называются эти уравнения?
-Правильно это линейные уравнения с одной переменной.
-А кто скажет определение линейного уравнения с одной переменной?
-Уравнение вида ах=в, в котором x- переменная, а а и
в – некоторые числа , называется линейным уравнением с одной переменной.
-Откройте учебники на стр. 27 , прочитайте это определение. Повтори.
-Приведите примеры линейных уравнений с одной переменной.
-Посмотрите на доску, перед вами линейные уравнения. Давайте вспомним как они
решаются.
-Откройте тетради, запишите число, классная работа, тема: «Линейные уравнения
с двумя переменными.»
-Все решают уравнения в тетрадях, а Оля пойдет к доске и решит с подробным
объяснением первое уравнение:
2х+6=10
(Перенесем слагаемое без х в правую часть уравнения, изменив при этом
его знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе
части уравнения на 2, получим х=2).
-Молодец. Садись.
-Второе уравнение пойдет решать Саша.
2(х+3)+4=х-1.
(Раскроем скобки, для этого умножим 2 на каждое слагаемое суммы (х+3), получим
2х+6+4=х-1. Перенесем слагаемые, содержащие х в левую часть уравнения,
а не содержащие х – в правую часть, изменив при этом знаки на
противоположные.
2х-х= -6-4-1.
Приведем подобные слагаемые : х= - 11.
- Ребята , такие уравнения вы хорошо умеете решать.
- А какие свойства применяли при решении этих уравнений? (Если в
уравнении слагаемое перенести из одной части в другую, изменив его знак , то
получится уравнение, равносильное данному.)
- А какое еще свойство вы применяли? (Если разделить или умножить обе
части уравнения на одно и тоже отличное от нуля число, то получится уравнение
равносильное данному.)
IV. Изучение нового материала.
-Ребята, а сегодня мы познакомимся с уравнениями нового вида.
-Пусть известно , что одно их двух чисел на 5 больше другого. Если первое число
обозначить буквой х, а второе буквой у, то соотношение между
ними можно записать в виде равенства х-у=5, содержащего 2 переменные. Такие
уравнения называются уравнениями с двумя переменными или уравнениями с двумя
неизвестными.
-Уравнениями с двумя переменными также являются уравнения:
5х+2у=10, -7х+у=5, х2+у2=20 , ху=12 (запись на доске).
-Из этих уравнений первые два имеют вид ах+ву=с, где а, в, с – числа.
Такие уравнения называются линейными уравнениями с двумя переменными.
-Итак: Линейным уравнением с двумя переменными называется уравнение вида
ах+ву=с где х и у – переменные, а, в, с, - некоторые
числа .
-Откройте учебники на странице 188.Прочитайте определение про себя.
-Теперь прочитайте вслух.
-А кто из вас повторит его ?
-уравнение х-у=5, при х=8, у=3. Обращается в верное равенство 8-3=5. Говорят,
что пара значений переменных х=8, у=3 является решением этого уравнения.
Записываю на доске:
х-у=5, х=8, у=3
8-3=5 - верное равенство.
Определение: Решением уравнения с двумя переменными называется пара
значений переменных, обращающая это уравнение в верное равенство.
-Прочитайте это определение на странице 188 про себя.
-Прочитайте его вслух.
-Кто повторит? Повтори.
-А какие еще пары чисел будут являться решениями уравнения х-у=5? (х=105,
у=100; х=4, у= -1,.)
-Правильно решениями этого уравнения будут являться числа, разность которых
равно 5.
-Иногда пары значений переменных записывают короче: (105; 100), (4;- 1). (
Запись на доске).
-При такой записи необходимо знать, значение какой из переменных стоит на
первом месте, а какой – на втором.
-в записи решений уравнения с переменными х и у на первом месте
записывают значения х, а на втором – значение у.
-Уравнения с двумя переменными имеющие одни и те же решения, называют
равносильными. уравнения с двумя переменными, не имеющие решений, также
считают равносильными.
-Ребята, при решении линейных уравнений с одной переменной мы вспомним их
свойства.
-Линейные уравнения с двумя переменными обладают такими же свойствами.
-Откройте учебники на стр. 189. Прочитайте эти свойства про себя.
-А теперь Таня , прочитай вслух. Повтори свойства.
-Рассмотрим уравнения 5х+2у=12.
-Воспользовались свойствами уравнений, выразим из этого уравнения одну
переменную через другую , например у, через х. Для этого
перенесем слагаемое 5х в правую часть уравнения изменив его знак.
2у= -5х+12.
-Разделим обе части этого уравнения на 2:
у= -2,5х+6
Уравнения 5х+2у=12 и
у= -2,5х+6 – равносильны.
-Пользуясь формулой у=2,5х+6, можно найти сколько угодно решений уравнения
5х+2у=12. Для этого достаточно взять произвольное х и вычислить
соответствующее ему значение у.
Например: если х=2 , то у= -2,5.2+6=1.
если х=0,4 то у= -2,5*0,4+4=5.
и биквадратные уравнения.
Еще один класс составляют алгебраические уравнения, которые разложением на
множители могут быть сведены к линейному и квадратному уравнениям. Богатство
и разнообразие приемов, имеющихся у учащихся, овладевших сведением различных
уравнений к квадратным, служат необходимой предпосылкой перехода к
завершающему этапу освоения методов решения уравнений. Особенно это
сказывается на приложении к алгебраическому методу решения текстовых задач.
Сюжеты их становятся более разнообразными, возрастает также сложность
перевода на язык математики. В целом можно сказать, что освоение темы
«Квадратные уравнения» поднимает учащихся на качественно новую ступень
овладения содержанием школьной математики.
Глава II. Методико - педагогические основы использования
самостоятельной работы, как средство обучения решению уравнений в 5 - 9
классах.
§ 1. Организация самостоятельной работы при обучения решению уравнений в
5 - 9 классах.
При традиционном способе преподавания учитель часто ставит ученика в
положение объекта передаваемой ему извне информации. Такой постановкой
образовательного процесса учитель искусственно задерживает развитие
познавательной активности ученика, наносит ему большой вред в
интеллектуальном и нравственном отношении.
«Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не
памятью», — эти слова Л. Н. Толстого должны стать смыслом работы учителя.
Самостоятельную деятельность учащихся можно и нужно организовывать на
различных уровнях: от воспроизведения действий по образцу и узнавания
объектов путем их сравнения с известным образцом до составления модели и
алгоритма действий в нестандартных ситуациях.
Учителю Необходимо учитывать, что при составлении заданий для самостоятельной
работы степень сложности должна отвечать учебным возможностям детей.
Переход с одного уровня на другой должен осуществляться постепенно, только
когда учитель будет убежден, что учащийся справится со следующим уровнем
самостоятельности. Иначе в атмосфере спешки и нервозности у ученика возникают
пробелы в знаниях.
Очень важно, чтобы содержание самостоятельной работы, форма и время ее
выполнения отвечали основным целям обучения данной теме на данном этапе.
В то же время учителю нужно знать, что злоупотребление самостоятельной
работой в учебном процессе также вредно, как и ее недооценка. Бывает так, что
учитель включает в урок самостоятельную работу без особой необходимости,
просто ради разнообразия, не продумав ее содержание и форму организации.
Результаты бывают плачевны: или дети не готовы выполнить задание, или не
хватило времени и т. п. А в результате — зря потрачено драгоценное время
урока. Но если, составляя план урока, учитель тщательно продумал место и
время самостоятельной работы; четко определил ее общее содержание, разбил
задания по разным уровням сложности, то она сыграет свою положительную роль.
Поэтому учителю очень важно знать формы и виды самостоятельных работ, их
место в процессе обучения.
Но нельзя забывать, что на успехи ученика огромное влияние оказывает настрой
самого учителя. Здесь очень важен известный психологам эффект Резенталя —
Якобсона. Эти исследователи провели следующий эксперимент: они давали
учителям заведомо неправильную информацию о показателях умственного развития
детей. Как выяснилось, последующие достижения учеников зависели от этой
информации, т. е. от мнения учителя о возможностях ученика. Те дети, которые
воспринимались учителем как более одаренные (хотя таковыми не являлись),
показали большие сдвиги в учебе по сравнению с детьми, которых учитель считал
менее одаренными.
Вот почему так важно умение учителя создать в классе доброжелательную
атмосферу, особенно во время выполнения самостоятельных работ.
В зависимости от целей, которые ставятся перед самостоятельными работами, они
могут быть:
1) обучающими;
2) тренировочными;
3) закрепляющими;
4) повторительными;
5) развивающими;
6) творческими;
7) контрольными.
1 Смысл обучающих самостоятельных работ заключается в
самостоятельном выполнении школьниками данных учителем заданий в ходе
объяснения нового материала. Цель таких работ — развитие интереса к изучаемому
материалу, привлечение внимания каждого ученика к тому, что объясняет учитель.
Здесь сразу выясняется непонятное, выявляются сложные моменты, дают себя знать
пробелы в знаниях, которые мешают прочно усвоить изучаемый материал.
Самостоятельные работы по формированию знаний проводятся на этапе подготовки
к введению нового содержания, а также при непосредственном введении нового
содержания, при первичном закреплении знаний, т. е. сразу после объяснения
нового, когда знания учащихся еще непрочны. Учителю необходимо знать
следующие особенности обучающих самостоятельных работ:
их надо составлять в основном из заданий репродуктивного характера, проверять
немедленно и не ставить за них плохих оценок.
Так как самостоятельные обучающие работы проводятся во время объяснения
нового материала или сразу после объяснения, то их немедленная проверка дает
учителю четкую картину того, что происходит на уроке, какова степень
понимания учащимися нового материала на самом раннем этапе его изучения. Цель
этих работ — не контроль, а обучение, поэтому им следует отводить много
времени на уроке.
Тема: «Линейное уравнение с двумя переменными».
Цель: 1. Дать понятие линейного уравнения с двумя переменными,
решения уравнения с двумя переменными; познакомить со свойствами уравнений с
двумя переменными; закрепить понятие линейного уравнения с одной переменной.
2. Развивать вычислительные навыки, речь, мышление, память.
3. Воспитывать самостоятельность активность , трудолюбие, любовь к математике.
Оборудование: карточку ax+by>c.
Ход урока.
I. Организационное начало урока.
-Здравствуйте, садитесь, сегодня урок алгебры проведу у вас я, зовут меня
Елена Федоровна
II. Сообщение темы и цели.
-Сегодня, на уроке мы познакомимся с уравнениями нового вида - «Линейными
уравнениями с двумя переменными».
III. Актуализация знаний учащихся.
-Посмотрите на доску. Какие из этих уравнений вам уже знакомы?
7х2+3х+5=0 5х+9=54
4х+9у=7 9(х2+6х+2)-8=30
x2/3+y2/2=1 4(х+2)+1=х+18.
-А как называются эти уравнения?
-Правильно это линейные уравнения с одной переменной.
-А кто скажет определение линейного уравнения с одной переменной?
-Уравнение вида ах=в, в котором x- переменная, а а и
в – некоторые числа , называется линейным уравнением с одной переменной.
-Откройте учебники на стр. 27 , прочитайте это определение. Повтори.
-Приведите примеры линейных уравнений с одной переменной.
-Посмотрите на доску, перед вами линейные уравнения. Давайте вспомним как они
решаются.
-Откройте тетради, запишите число, классная работа, тема: «Линейные уравнения
с двумя переменными.»
-Все решают уравнения в тетрадях, а Оля пойдет к доске и решит с подробным
объяснением первое уравнение:
2х+6=10
(Перенесем слагаемое без х в правую часть уравнения, изменив при этом
его знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе
части уравнения на 2, получим х=2).
-Молодец. Садись.
-Второе уравнение пойдет решать Саша.
2(х+3)+4=х-1.
(Раскроем скобки, для этого умножим 2 на каждое слагаемое суммы (х+3), получим
2х+6+4=х-1. Перенесем слагаемые, содержащие х в левую часть уравнения,
а не содержащие х – в правую часть, изменив при этом знаки на
противоположные.
2х-х= -6-4-1.
Приведем подобные слагаемые : х= - 11.
- Ребята , такие уравнения вы хорошо умеете решать.
- А какие свойства применяли при решении этих уравнений? (Если в
уравнении слагаемое перенести из одной части в другую, изменив его знак , то
получится уравнение, равносильное данному.)
- А какое еще свойство вы применяли? (Если разделить или умножить обе
части уравнения на одно и тоже отличное от нуля число, то получится уравнение
равносильное данному.)
IV. Изучение нового материала.
-Ребята, а сегодня мы познакомимся с уравнениями нового вида.
-Пусть известно , что одно их двух чисел на 5 больше другого. Если первое число
обозначить буквой х, а второе буквой у, то соотношение между
ними можно записать в виде равенства х-у=5, содержащего 2 переменные. Такие
уравнения называются уравнениями с двумя переменными или уравнениями с двумя
неизвестными.
-Уравнениями с двумя переменными также являются уравнения:
5х+2у=10, -7х+у=5, х2+у2=20 , ху=12 (запись на доске).
-Из этих уравнений первые два имеют вид ах+ву=с, где а, в, с – числа.
Такие уравнения называются линейными уравнениями с двумя переменными.
-Итак: Линейным уравнением с двумя переменными называется уравнение вида
ах+ву=с где х и у – переменные, а, в, с, - некоторые
числа .
-Откройте учебники на странице 188.Прочитайте определение про себя.
-Теперь прочитайте вслух.
-А кто из вас повторит его ?
-уравнение х-у=5, при х=8, у=3. Обращается в верное равенство 8-3=5. Говорят,
что пара значений переменных х=8, у=3 является решением этого уравнения.
Записываю на доске:
х-у=5, х=8, у=3
8-3=5 - верное равенство.
Определение: Решением уравнения с двумя переменными называется пара
значений переменных, обращающая это уравнение в верное равенство.
-Прочитайте это определение на странице 188 про себя.
-Прочитайте его вслух.
-Кто повторит? Повтори.
-А какие еще пары чисел будут являться решениями уравнения х-у=5? (х=105,
у=100; х=4, у= -1,.)
-Правильно решениями этого уравнения будут являться числа, разность которых
равно 5.
-Иногда пары значений переменных записывают короче: (105; 100), (4;- 1). (
Запись на доске).
-При такой записи необходимо знать, значение какой из переменных стоит на
первом месте, а какой – на втором.
-в записи решений уравнения с переменными х и у на первом месте
записывают значения х, а на втором – значение у.
-Уравнения с двумя переменными имеющие одни и те же решения, называют
равносильными. уравнения с двумя переменными, не имеющие решений, также
считают равносильными.
-Ребята, при решении линейных уравнений с одной переменной мы вспомним их
свойства.
-Линейные уравнения с двумя переменными обладают такими же свойствами.
-Откройте учебники на стр. 189. Прочитайте эти свойства про себя.
-А теперь Таня , прочитай вслух. Повтори свойства.
-Рассмотрим уравнения 5х+2у=12.
-Воспользовались свойствами уравнений, выразим из этого уравнения одну
переменную через другую , например у, через х. Для этого
перенесем слагаемое 5х в правую часть уравнения изменив его знак.
2у= -5х+12.
-Разделим обе части этого уравнения на 2:
у= -2,5х+6
Уравнения 5х+2у=12 и
у= -2,5х+6 – равносильны.
-Пользуясь формулой у=2,5х+6, можно найти сколько угодно решений уравнения
5х+2у=12. Для этого достаточно взять произвольное х и вычислить
соответствующее ему значение у.
Например: если х=2 , то у= -2,5.2+6=1.
если х=0,4 то у= -2,5*0,4+4=5.
Пары чисел (2; 1), (0,4; 5) – решение уравнения 5х+2у=12.
Это уравнение имеет бесконечно много решений.
V .Первичное закрепление.
-Что же называется линейным уравнением с двумя переменными?
-Выполним № 1092 на странице 190 устно.
-Прочитай задание.
-Является ли первое уравнение 3х-у=17 линейным? (Да).
-Почему? (Т.к. имеет вид ах+ву=с)
-А второе упражнение? (Нет).
-Почему? (Т.к. уравнение х2- 2у=5 не приводится к виду ах+ву=с, х
имеет показатель степени 2).
(Далее аналогично).
-А теперь запишите № 1094.
-Читай задание .
-Как ответить на этот вопрос? (Поставить значение х и у в
уравнение. Если получится верное равенство, то х и у является
решением уравнения)
-Все решайте в тетрадях, а... у доски.
х + у=6
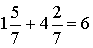
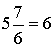 6=6 – верное равенство.
Ответ: да.
-А какие еще числа могут быть решениями этого уравнения х+у=6. (Дающие в
сумме 6: 4 и 2, 3 и 3 и т.д.).
-Запишите любые 2 решения этого уравнения.
-Не забывайте, что значение х пишется на первом месте а у – на втором месте.
Самостоятельная работа.
-А теперь выполним № 1096. запишите.
-Прочитай задание.
-Что нужно сделать, чтобы ответить на вопрос? (Подставить значения х и
у в уравнение и посмотреть, получится ли верное равенство).
а) .Организация самостоятельной работы.
-Все решают в тетрадях, а к доске пойдут Лена и Оля.
-Саша проверит первые 2 пары, а Катя вторые 2 пары.
-А потом проверим.
б) Проведение самостоятельной работы.
(3; 1 ) (0; 10)
3*3+1>10 3*0+10=10.
10=10 – верное равенство 10=10 верное равенство
Ответ: является Ответ: является
(2; 4) (3; 2,5)
3*2+4=10 3*3+2.5=10
10=10 – верное равенство 11,5=10 – неверное равенство
Ответ: является Ответ: не является.
в) Проверка самостоятельной работы.
-Давайте проверим правильно ли выполнила Оля.
-У кого другой ответ?
-А Лена?
-У кого другой ответ?
-Молодцы. Садитесь.
-А теперь выполним № 1099.
-Прочитай задание.
-Что нужно сделать, чтобы выразить у через х? (Представить, что
х известное число и найти у )
-Пойди к доске реши с объяснением, а все решают в тетрадях.
4х-3у=12.
(Одночлен 3у является неизвестным вычитаемым. Чтобы найти неизвестное
вычитаемое, надо из уменьшаемого вычесть разность 3у=4х-12 .
Разделим обе части уравнения на 3, получим:
6=6 – верное равенство.
Ответ: да.
-А какие еще числа могут быть решениями этого уравнения х+у=6. (Дающие в
сумме 6: 4 и 2, 3 и 3 и т.д.).
-Запишите любые 2 решения этого уравнения.
-Не забывайте, что значение х пишется на первом месте а у – на втором месте.
Самостоятельная работа.
-А теперь выполним № 1096. запишите.
-Прочитай задание.
-Что нужно сделать, чтобы ответить на вопрос? (Подставить значения х и
у в уравнение и посмотреть, получится ли верное равенство).
а) .Организация самостоятельной работы.
-Все решают в тетрадях, а к доске пойдут Лена и Оля.
-Саша проверит первые 2 пары, а Катя вторые 2 пары.
-А потом проверим.
б) Проведение самостоятельной работы.
(3; 1 ) (0; 10)
3*3+1>10 3*0+10=10.
10=10 – верное равенство 10=10 верное равенство
Ответ: является Ответ: является
(2; 4) (3; 2,5)
3*2+4=10 3*3+2.5=10
10=10 – верное равенство 11,5=10 – неверное равенство
Ответ: является Ответ: не является.
в) Проверка самостоятельной работы.
-Давайте проверим правильно ли выполнила Оля.
-У кого другой ответ?
-А Лена?
-У кого другой ответ?
-Молодцы. Садитесь.
-А теперь выполним № 1099.
-Прочитай задание.
-Что нужно сделать, чтобы выразить у через х? (Представить, что
х известное число и найти у )
-Пойди к доске реши с объяснением, а все решают в тетрадях.
4х-3у=12.
(Одночлен 3у является неизвестным вычитаемым. Чтобы найти неизвестное
вычитаемое, надо из уменьшаемого вычесть разность 3у=4х-12 .
Разделим обе части уравнения на 3, получим:
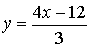 -Молодец. Садись.
А теперь выполним пункт б, Сережа иди к доске.
4х-3у=12.
(Одночлен 4х является неизвестным уменьшаемым, чтобы его найти, надо к разности
прибавить вычитаемое: 4х=12+3у. Разделим обе части уравнения на 4 и получим:
-Молодец. Садись.
А теперь выполним пункт б, Сережа иди к доске.
4х-3у=12.
(Одночлен 4х является неизвестным уменьшаемым, чтобы его найти, надо к разности
прибавить вычитаемое: 4х=12+3у. Разделим обе части уравнения на 4 и получим: 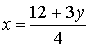 -Правильно. Молодец. Садись .
VI. Подведение итогов.
-Какой вид имеет линейное уравнение с двумя переменными ? (ах+ву=с).
-Что называется решением линейного уравнения с двумя переменными ?
-Приведите примеры таких уравнений.
-Какими свойствами обладают уравнения с двумя переменными?
2 К тренировочным относятся задания на распознавание различных
объектов и их свойств. Тренировочные самостоятельные работы состоят из
однотипных заданий, содержащих существенные признаки и свойства данного
определения, правила. Конечно, эта работа мало способствует умственному
развитию детей, но она необходима, так как позволяет выработать основные умения
и навыки и тем самым создать базу для дальнейшего изучения математики.
При выполнении тренировочных самостоятельных работ учащимся еще необходима
помощь учителя. Можно разрешить пользоваться и учебником, и записями в
тетрадях, таблицами и т. п. Все это создает благоприятный климат для слабых
учащихся. В таких условиях они очень легко включаются в работу и выполняют
ее.
-Правильно. Молодец. Садись .
VI. Подведение итогов.
-Какой вид имеет линейное уравнение с двумя переменными ? (ах+ву=с).
-Что называется решением линейного уравнения с двумя переменными ?
-Приведите примеры таких уравнений.
-Какими свойствами обладают уравнения с двумя переменными?
2 К тренировочным относятся задания на распознавание различных
объектов и их свойств. Тренировочные самостоятельные работы состоят из
однотипных заданий, содержащих существенные признаки и свойства данного
определения, правила. Конечно, эта работа мало способствует умственному
развитию детей, но она необходима, так как позволяет выработать основные умения
и навыки и тем самым создать базу для дальнейшего изучения математики.
При выполнении тренировочных самостоятельных работ учащимся еще необходима
помощь учителя. Можно разрешить пользоваться и учебником, и записями в
тетрадях, таблицами и т. п. Все это создает благоприятный климат для слабых
учащихся. В таких условиях они очень легко включаются в работу и выполняют
ее.
Тема: | Решение текстовых задач при помощи систем уравнений, содержащих уравнения второй степени. | | | Цель: | Расширение и углубление знаний, формирование умений решать системы, повышенной сложности, уметь составлять системы по условию задачи: Развивать устойчивый интерес к предмету, умение самостоятельно работать; Воспитывать умение осуществлять индивидуальную мыслительную деятельность; | Оборудование: | Учебник, «сборники заданий по математике» Кузнецов Л. В.; |
Ход урока:
I. Организационное начало урока:
II. Сообщение темы и цели: - Сегодня на уроке продолжим
решать системы уравнений, но будем учиться сами составлять по задаче систему.
III. Актуализация знаний учащихся: - Запишите число, тему.
1) выразить одну неизвестную через другую:
1. 3х-у=3 -у=3-3х у=3х-3 | 2. у+2х=2 2х=2-у 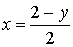
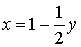
| | | 2) решить систему методом подстановки: | | - Повторим алгоритм. Решим: | 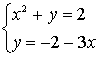
| 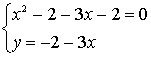
| 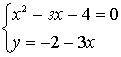
| |
Решим квадратное уравнение:
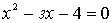
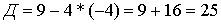
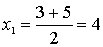 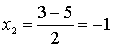
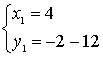 или или 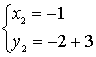
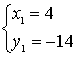 или или 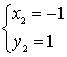 Ответ: (4; -14); (-1; 1)
IV. Закрепление
№ 498
-Прочтите задачу
-Как обозначим числа? (х, у)
-Если сумма? (х+у=18)
-Произведение чисел? (х*у=65)
-Найти что? (эти числа)
-Какую систему получим?
-Каким методом будем решать?
Ответ: (4; -14); (-1; 1)
IV. Закрепление
№ 498
-Прочтите задачу
-Как обозначим числа? (х, у)
-Если сумма? (х+у=18)
-Произведение чисел? (х*у=65)
-Найти что? (эти числа)
-Какую систему получим?
-Каким методом будем решать?
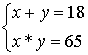 (записать пояснение: Пусть первое число – х и т. д.)
-К доске пойдет.. (записать пояснение: Пусть первое число – х и т. д.)
-К доске пойдет..
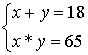 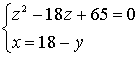 Решим квадратное уравнение:
Решим квадратное уравнение:
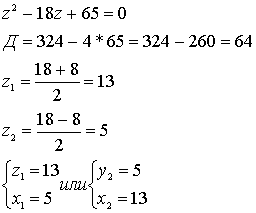 Ответ: числа 5 и 13.
№504
-Прочтите условие.
-Какой формы участок? (Прямоугольной)
-Пусть длина – х, ширина – у.
-Площадь прямоугольника? (S=ав)
-Нужно перевести в одну единицу измерения: км. в м., га. в м2;
-Если участок прямоугольной формы, то какое уравнение составим?
(2(х+у)=1000)
-Площадь участка 60000 м2? (ху=60000)
-Запишем условие к задаче:
Пусть длина участка – х, ширина – у. Так как участок надо огородить забором
длиной 1000м. Так как площадь участка 60000 м2, то составим
уравнение: ху=60000. Получим систему:
Ответ: числа 5 и 13.
№504
-Прочтите условие.
-Какой формы участок? (Прямоугольной)
-Пусть длина – х, ширина – у.
-Площадь прямоугольника? (S=ав)
-Нужно перевести в одну единицу измерения: км. в м., га. в м2;
-Если участок прямоугольной формы, то какое уравнение составим?
(2(х+у)=1000)
-Площадь участка 60000 м2? (ху=60000)
-Запишем условие к задаче:
Пусть длина участка – х, ширина – у. Так как участок надо огородить забором
длиной 1000м. Так как площадь участка 60000 м2, то составим
уравнение: ху=60000. Получим систему:
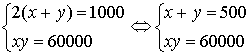
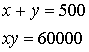 Þ Þ 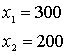
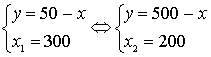
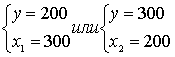 Ответ: длина – 300м., ширина – 200м.
№ 1
-Послушайте условие:
«Одно из двух положительных чисел на 3 больше другого. Найдите эти числа,
если их произведение равно 70?»
-Пусть числа х и у.
-Если известно, что одно больше на 3. Как запишем? (х=у+3)
-Произведение чисел? (ху=70)
-Составим систему:
Ответ: длина – 300м., ширина – 200м.
№ 1
-Послушайте условие:
«Одно из двух положительных чисел на 3 больше другого. Найдите эти числа,
если их произведение равно 70?»
-Пусть числа х и у.
-Если известно, что одно больше на 3. Как запишем? (х=у+3)
-Произведение чисел? (ху=70)
-Составим систему:
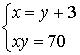 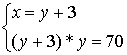
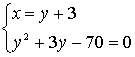 Решим квадратное уравнение:
Решим квадратное уравнение:
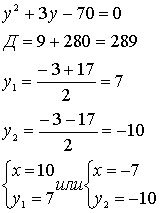 так как числа положительные, то 10 и 7.
Ответ: 10 и 7.
2) самостоятельная работа. (15 мин.)
-У вас на партах лежат сборники заданий и у каждого номер индивидуального
задания.
-Запишите: «Самостоятельная работа»., стр. №..
так как числа положительные, то 10 и 7.
Ответ: 10 и 7.
2) самостоятельная работа. (15 мин.)
-У вас на партах лежат сборники заданий и у каждого номер индивидуального
задания.
-Запишите: «Самостоятельная работа»., стр. №..
1. | С. 15, в-1, № 3 С. 11, в-1, №4 | 2. | С. 20, в-1, № 5 С. 19, в-1, №4 | 3. | С. 28, в-1, № 6 С. 11, в-1, №4 | 4 | С. 35, в-1, № 3 С. 19, в-1, №4 | 5. | С. 48, в-1, № 6 С. 19, в-1, №4 | 6 | С. 21, в-1, № 6 С. 19, в-2, №4 | 7. | С. 15, в-2, № 3 С. 11, в-2, №4 | 8. | С. 20, в-2, № 5 С. 19, в-2, №4 | 9. | С. 28, в-2, № 6 С. 11, в-2, №4 | 10. | С. 35, в-2, № 3 С. 19, в-2, №4 | 11. | С. 48, в-2, № 6 С. 19, в-2, №4 | 12. | С. 21, в-2, № 6 С. 11, в-1, №4 | 13. | С. 29, в-1, № 4 С. 11, в-1, №4 | 14. | С. 29, в-2, № 4 С. 11, в-1, №4 | 15. | С. 30, в-2, № 6 С. 11, в-2, №4 | 16. | С. 31, в-2, № 6 С. 19, в-1, №4 | 17. | С. 30, в-1, № 6 С. 19, в-2, №4 | 18. | С. 31, в-1, № 6 С. 11, в-1, №4 |
Страницы: 1, 2, 3
|

|

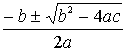 ».
Учитывая этот вывод, решение конкретных квадратных уравнений проводится
следующим образом: сначала вычисляется дискриминант, сравнивается с нулем, и
если он неотрицателен, то применяются формулы для нахождения корней.
В ряде учебников, кроме основной формулы для корней квадратного уравнения ах
2 + bх + с = 0, приводятся еще формулы корней уравнения x2
+px+q=0 или x2+2px+q=0. Иногда использование этих формул
упрощает вычисления, при наличии времени полезно их рассмотреть.
При изучении темы «Квадратные уравнения» рассматриваются и неполные
квадратные уравнения. Обычно они изучаются перед выводом корней общего
квадратного уравнения. Хотя различные виды неполных квадратных уравнении
имеют разные алгоритмы решения, при изучении данной темы необходимо показать,
что общая формула корней применима и для этих случаев.
Важным моментом в изучении квадратных уравнений является рассмотрение теоремы
Виета, которая утверждает наличие зависимости между корнями и коэффициентами
квадратного уравнения. Сложность освоения теоремы Виета связана с несколькими
обстоятельствами. Прежде всего требуется учитывать различие прямой и обратной
теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в
обратной — только два числа, а квадратное уравнение появляется в заключении
теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения
неверной ссылкой на прямую или обратную теорему Виета. Например, при
нахождении корней квадратного уравнения подбором ссылаться нужно на обратную
теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы
распространить теоремы Виета на случай нулевого дискриминанта, приходится
условиться, что в этом случае квадратное уравнение имеет два равных корня.
Удобство такого соглашения проявляется при разложении квадратного трехчлена
на множители.
Владение теорией квадратных уравнений существенно расширяет возможности решения
уравнений методами, изучаемыми в курсе алгебры. Так, прямо сводятся к
квадратным дробно-рациональные уравнения вида
».
Учитывая этот вывод, решение конкретных квадратных уравнений проводится
следующим образом: сначала вычисляется дискриминант, сравнивается с нулем, и
если он неотрицателен, то применяются формулы для нахождения корней.
В ряде учебников, кроме основной формулы для корней квадратного уравнения ах
2 + bх + с = 0, приводятся еще формулы корней уравнения x2
+px+q=0 или x2+2px+q=0. Иногда использование этих формул
упрощает вычисления, при наличии времени полезно их рассмотреть.
При изучении темы «Квадратные уравнения» рассматриваются и неполные
квадратные уравнения. Обычно они изучаются перед выводом корней общего
квадратного уравнения. Хотя различные виды неполных квадратных уравнении
имеют разные алгоритмы решения, при изучении данной темы необходимо показать,
что общая формула корней применима и для этих случаев.
Важным моментом в изучении квадратных уравнений является рассмотрение теоремы
Виета, которая утверждает наличие зависимости между корнями и коэффициентами
квадратного уравнения. Сложность освоения теоремы Виета связана с несколькими
обстоятельствами. Прежде всего требуется учитывать различие прямой и обратной
теоремы. В прямой теореме Виета даны квадратное уравнение и его корни; в
обратной — только два числа, а квадратное уравнение появляется в заключении
теоремы. Учащиеся часто совершают ошибку, обосновывая свои рассуждения
неверной ссылкой на прямую или обратную теорему Виета. Например, при
нахождении корней квадратного уравнения подбором ссылаться нужно на обратную
теорему Виета, а не на прямую, как часто делают учащиеся. Для того чтобы
распространить теоремы Виета на случай нулевого дискриминанта, приходится
условиться, что в этом случае квадратное уравнение имеет два равных корня.
Удобство такого соглашения проявляется при разложении квадратного трехчлена
на множители.
Владение теорией квадратных уравнений существенно расширяет возможности решения
уравнений методами, изучаемыми в курсе алгебры. Так, прямо сводятся к
квадратным дробно-рациональные уравнения вида 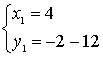 или
или 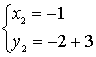
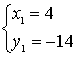 или
или 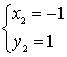 Ответ: (4; -14); (-1; 1)
IV. Закрепление
№ 498
-Прочтите задачу
-Как обозначим числа? (х, у)
-Если сумма? (х+у=18)
-Произведение чисел? (х*у=65)
-Найти что? (эти числа)
-Какую систему получим?
-Каким методом будем решать?
Ответ: (4; -14); (-1; 1)
IV. Закрепление
№ 498
-Прочтите задачу
-Как обозначим числа? (х, у)
-Если сумма? (х+у=18)
-Произведение чисел? (х*у=65)
-Найти что? (эти числа)
-Какую систему получим?
-Каким методом будем решать?
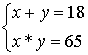 (записать пояснение: Пусть первое число – х и т. д.)
-К доске пойдет..
(записать пояснение: Пусть первое число – х и т. д.)
-К доске пойдет..
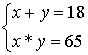
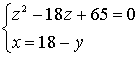 Решим квадратное уравнение:
Решим квадратное уравнение:
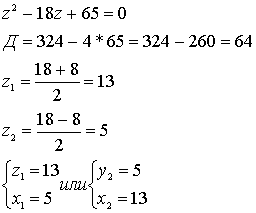 Ответ: числа 5 и 13.
№504
-Прочтите условие.
-Какой формы участок? (Прямоугольной)
-Пусть длина – х, ширина – у.
-Площадь прямоугольника? (S=ав)
-Нужно перевести в одну единицу измерения: км. в м., га. в м2;
-Если участок прямоугольной формы, то какое уравнение составим?
(2(х+у)=1000)
-Площадь участка 60000 м2? (ху=60000)
-Запишем условие к задаче:
Пусть длина участка – х, ширина – у. Так как участок надо огородить забором
длиной 1000м. Так как площадь участка 60000 м2, то составим
уравнение: ху=60000. Получим систему:
Ответ: числа 5 и 13.
№504
-Прочтите условие.
-Какой формы участок? (Прямоугольной)
-Пусть длина – х, ширина – у.
-Площадь прямоугольника? (S=ав)
-Нужно перевести в одну единицу измерения: км. в м., га. в м2;
-Если участок прямоугольной формы, то какое уравнение составим?
(2(х+у)=1000)
-Площадь участка 60000 м2? (ху=60000)
-Запишем условие к задаче:
Пусть длина участка – х, ширина – у. Так как участок надо огородить забором
длиной 1000м. Так как площадь участка 60000 м2, то составим
уравнение: ху=60000. Получим систему:
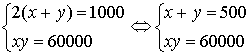
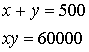 Þ
Þ 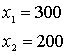
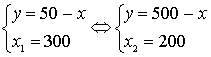
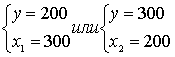 Ответ: длина – 300м., ширина – 200м.
№ 1
-Послушайте условие:
«Одно из двух положительных чисел на 3 больше другого. Найдите эти числа,
если их произведение равно 70?»
-Пусть числа х и у.
-Если известно, что одно больше на 3. Как запишем? (х=у+3)
-Произведение чисел? (ху=70)
-Составим систему:
Ответ: длина – 300м., ширина – 200м.
№ 1
-Послушайте условие:
«Одно из двух положительных чисел на 3 больше другого. Найдите эти числа,
если их произведение равно 70?»
-Пусть числа х и у.
-Если известно, что одно больше на 3. Как запишем? (х=у+3)
-Произведение чисел? (ху=70)
-Составим систему:
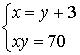
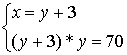
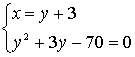 Решим квадратное уравнение:
Решим квадратное уравнение:
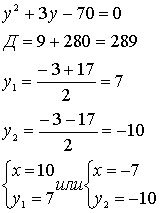 так как числа положительные, то 10 и 7.
Ответ: 10 и 7.
2) самостоятельная работа. (15 мин.)
-У вас на партах лежат сборники заданий и у каждого номер индивидуального
задания.
-Запишите: «Самостоятельная работа»., стр. №..
так как числа положительные, то 10 и 7.
Ответ: 10 и 7.
2) самостоятельная работа. (15 мин.)
-У вас на партах лежат сборники заданий и у каждого номер индивидуального
задания.
-Запишите: «Самостоятельная работа»., стр. №..